柏林噪聲實現2D圖像霧

實現效果如下
在这里插入图片描述

在这里插入图片描述

Perlin噪聲的原理
https://mrl.nyu.edu/~perlin/doc/oscar.html
論文作者
來自騰訊游戲學院（算是寫的我能看懂的了）
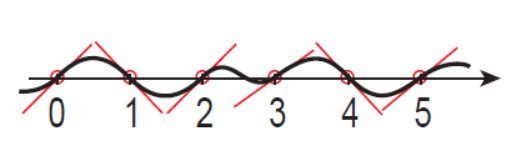
1、一维柏林噪声
　　首先，在X轴向上每个整数坐标随机生成一个数（范围为-1~1），我们称这个数为Gradient，译为梯度或者斜率。然后我们对相邻两个整数之间使用梯度进行插值计算，使得相邻两点之间平滑过渡。平滑度取决于所选用的插值函数，老版的柏林噪声使用f(t)=3tt-2ttt，改进后的柏林噪声使用f(t)=ttt(t*(t*6-15)+10)。（代碼裏會用到）
在这里插入图片描述
2、二维柏林噪声
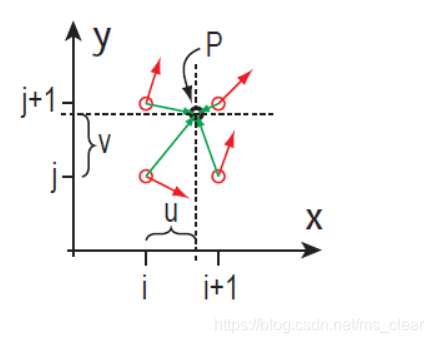
对于二维来说我们可以获取点P(x, y)最近的四个整数点ABCD，ABCD四个点的坐标分别为A(i, j)、B(i+1, j)、C(i, j+1)、D(i+1, j+1)，随后获取ABCD四点的二维梯度值G(A)、G(B)、G©、G(D)，并且算出ABCD到P点的向量AP、BP、CP以及DP。如下图所示：
在这里插入图片描述
　　红色箭头表示该点处的梯度值，绿色箭头表示该点到P点的向量。
　　接着，将G(A)与AP进行点乘，计算出A点对于P点的梯度贡献值，然后分别算出其余三个点对P点的梯度贡献值，最后将(u, v)代入插值函数中算出P点的最终噪声值。
　　以上类推到三维的柏林噪声，则需要算出八个顶点的梯度贡献值，然后进行插值计算。
　　还有一个问题没有解决，就是怎样随机生成梯度值。当然你可以通过使用一个伪随机函数生成一维到三维的梯度值（二维和三维就是梯度向量了），例如，对于一维可以使用下面的公式：
　　Fract(Sin(n)*753.5453123f);

代碼實現

Shader "Hidden/TextFogShader"
{
   
	Properties
	{
   
		_MainTex("Texture", 2D) = "white" {
   }//紋理
		_Color("Fog Color", Color) = (1,1,1,1)//霧的顔色
		_Scale("Fog scale"

柏林噪聲實現2D圖像霧

悦读