二分算法
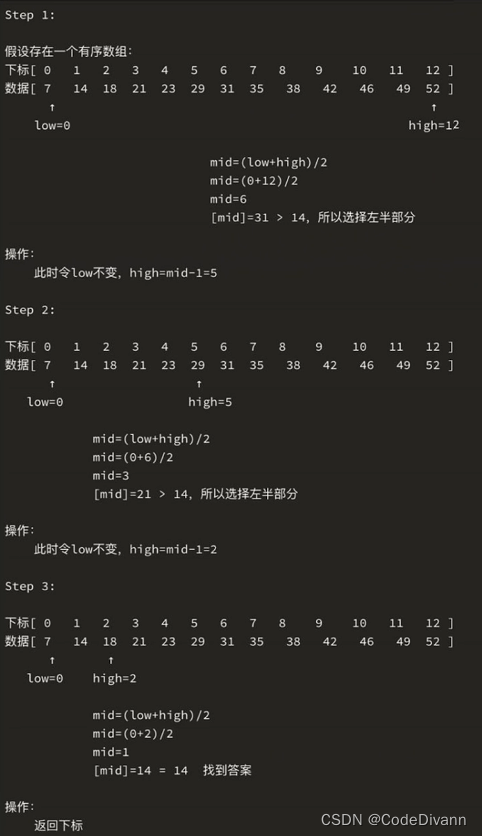
整数二分算法模板
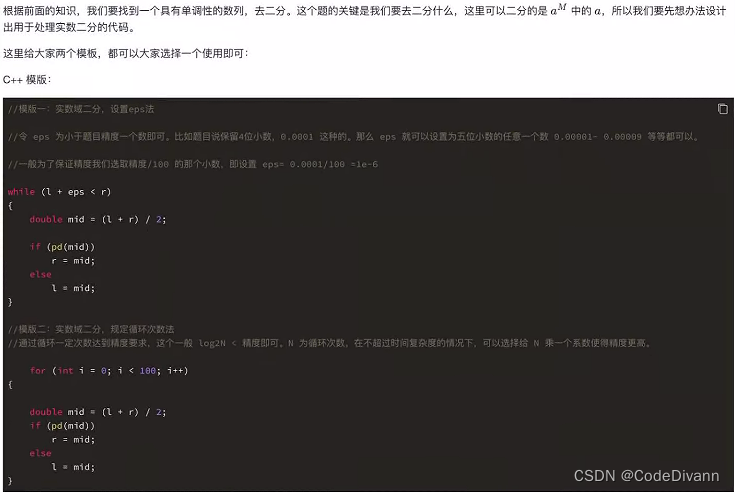
实数二分算法模板(二选一)
题目:M次方根(实数)
#include<bits/stdc++.h>
using namespace std;
double n, l, r, mid; // 定义需要的变量,n为目标数,l和r为二分的左右边界,mid为中间值
double eps = 1e-8; // 精度设定为1e-8
// 判断a的m次方是否大于等于n
bool pd(double a, int m) {
double c = 1;
// 迭代计算a的m次方
while (m > 0) {
c = c * a;
m--;
}
// 如果计算结果大于等于n,返回true,否则返回false
if (c >= n)
return true;
else
return false;
}
int main() {
int m; // 输入的次数
cin >> n >> m; // 输入目标数n和次数m
// 设置二分搜索的边界为[0, n]
l = 0, r = n;
// 实数二分搜索
while (l + eps < r) {
// 取当前二分搜索的中点
double mid = (l + r) / 2;
// 判断当前中点的m次方是否大于等于n
if (pd(mid, m))
r = mid; // 如果大于等于n,则将搜索范围缩小到左半部分
else
l = mid; // 如果小于n,则将搜索范围缩小到右半部分
}
// 输出结果,精度为7位小数
printf("%.7lf", l);
return 0;
}
题目:分巧克力(整数)
2 10 6 5 5 6
#include<bits/stdc++.h>
using namespace std;
const int Maxn=10010;
int n,k;// 输入的数目n和要求的正方形数量k
int h[Maxn],w[Maxn];// 分别表示每个矩形的高度和宽度
bool pd(int l){ // 判断是否满足条件的函数,参数l表示正方形的边长
int sum=0; // 总共可以切出的正方形数量
for(int i=0;i<n;i++){ // 遍历每个矩形
sum=sum+(h[i]/l)*(w[i]/l); // 计算当前矩形可以切出的正方形数量,并累加到总数中
if(sum>=k) // 如果总数已经达到或超过要求的数量k
return true; // 返回true,表示当前边长满足条件
}
return false; // 如果循环结束仍未达到要求的数量k,则返回false
}
int main(){
cin>>n>>k; // 输入矩形的数目n和要求的正方形数量k
for(int i=0;i<n;i++){ // 输入每个矩形的高度和宽度
cin>>h[i]>>w[i];
}
//找到二分查找的上界
int high=0; // 初始化二分查找的上界为0
for(int i=0;i<n;i++){ // 遍历每个矩形
high=max(high,h[i]); // 更新上界为所有矩形中高度和宽度的最大值
high=max(high,w[i]);
}
//二分下界由题意可得至少为1
int low=1; // 初始化二分查找的下界为1
//由于本题就是求符合要求的Mid值,所以要将mid定义在二分查找外边
int mid=0; // 初始化mid变量
while(low<high){ // 当下界小于上界时循环
mid=(low+high+1)/2; // 计算mid值,向上取整
if(pd(mid)) // 判断当前mid值是否满足条件
low=mid; // 如果满足条件,则更新下界为mid
else
high=mid-1; // 如果不满足条件,则更新上界为mid-1
}
cout<<low; // 输出满足条件的最大边长
return 0;
}题目:跳石头
25 5 2 2 11 14 17 21
#include <stdio.h>
int main(){
int len,n,m;
int a[50005],temp,before=0;
scanf("%d %d %d",&len,&n,&m);
for(int i=0;i<n;i++)
{
scanf("%d",&temp);//记录当前位置
a[i]=temp-before;//记录两个石头间的距离
before=temp; //记录上一个石头位置
}
a[n]=len-before;
if(n==m){//特殊情况直接输出
printf("%d",len);
return 0;
}
int r=len/(n-m),l=1,tp;// l 表示所求值的最小值,r为所求值的最大值
//因为将总长度等分就是所求长度的最大值
while(l<=r){//进行二分查找
int mid=(l+r)/2,count=0;
for(int i=0;i<=n;i++)
{ tp=a[i];
while(tp<mid&&i<n){
i++;
tp+=a[i];
count++;//记录移除石头数目
}
}
if(count<=m) l=mid+1;//若移除数目小于等于规定数目表明mid小于等于所求值,进行下一步查找
else r=mid-1;//mid大于所求值,缩小范围
}
printf("%d",r);
return 0;
}