【教程】python递归三部曲（基于turtle实现可视化）-二、汉诺塔

递归三部曲：

二、汉诺塔

1、汉诺塔

本教程为本人在b站投稿的视频教程对应的文字版
视频较详细，文本较简洁，大家选择一个看就好

汉诺塔(Tower of Hanoi)：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。
大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

抽象成数学问题如下：
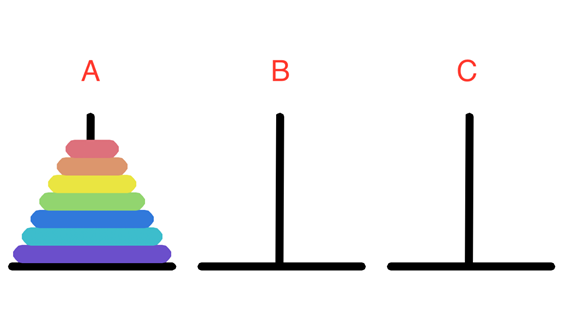
有三根相邻的柱子，标号为A,B,C
A柱子上从下到上按金字塔状叠放着n个大小不同（下面的大于上面）的圆盘
要把所有盘子一个一个移动到柱子C上(每次移动时，同一根柱子上小盘子都要在大的圆盘上面)
点击观看移动动画
n=7

2、思路分析

移动过程

A塔是圆盘出发的塔，称之为起点塔
C塔是圆盘最终要达到的塔，称之为目标塔
B塔起辅助中转作用，称之为中转塔
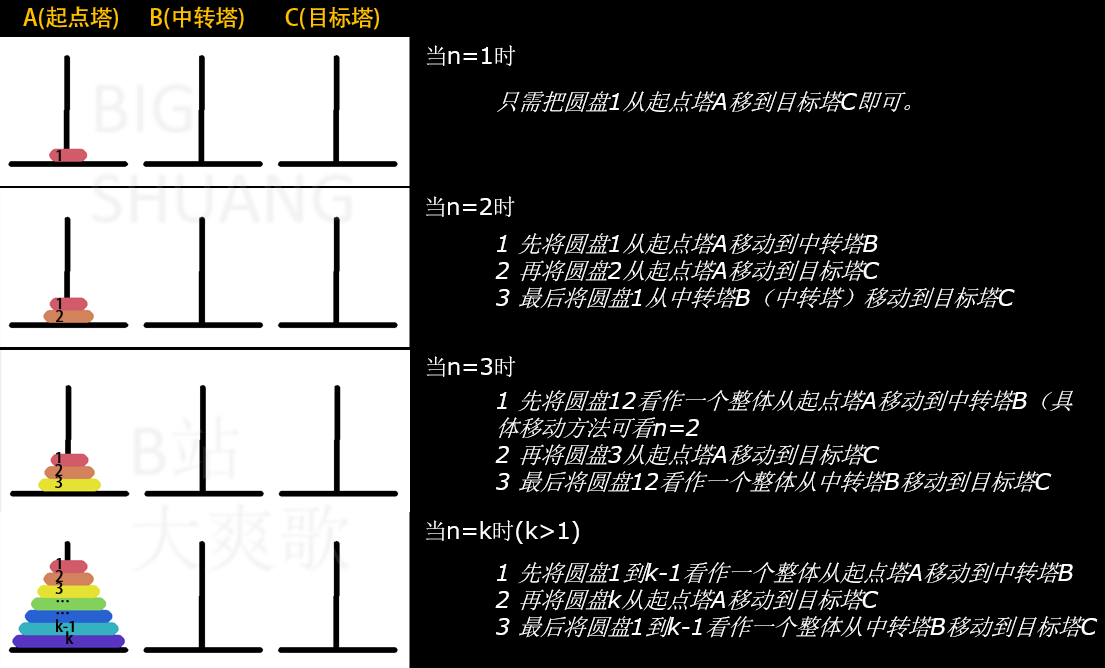
那么各种层数n下，圆盘移动过程分析如图
在这里插入图片描述

代码

首先，需要添加方法moveTower来绘制指定层数的谢尔宾斯基三角形

def moveTower(height, fromPole, withPole, toPole):
	"""
	:param height: 汉诺塔高度——层数，设为N
	:param fromPole: 出发的柱子（起点塔A）
	:param withPole: 经过的柱子（中转塔B）,起辅助作用
	:param toPole: 要到达的柱子（目标塔C）
	"""

然后我们再分析下moveTower方法应该怎么写
1、只有一层的话，直接将圆盘1从起点塔A移动到目标塔C
否则的话
2、将圆盘1到n - 1看作一个整体，从起点塔A借助目标塔C移动到中转塔B
3、再将圆盘n从起点塔A移动到目标塔C
4、将圆盘1到n - 1看作一个整体，从中转塔B借助起点塔A移动到目标塔C
为了实现上面四步，我们需要添加一个辅助方法
moveDisk(diskIndex,fromPole,toPole) : 移动指定层圆盘diskIndex，从fromPole出发，到达toPole
我们先通过简单的控制台输出实现汉诺塔，代码如下

def moveDisk(diskIndex, fromPole, toPole):
	print_str = 'Move disk %s form %s to %s' % (diskIndex, fromPole, toPole)
	print(print_str)

def moveTower(height, fromPole, withPole, toPole):
	"""
	:param height: 汉诺塔高度——层数，设为N
	:param fromPole: 出发的柱子（起点塔A）
	:param withPole: 经过的柱子（中转塔B）,起辅助作用
	:param toPole: 要到达的柱子（目标塔C）
	"""
	if height == 1 :
		moveDisk(1, fromPole, toPole)
	else:
		moveTower(height-1, fromPole, toPole, withPole)
		moveDisk(height, fromPole, toPole)
		moveTower(height-1, withPole, fromPole, toPole)

if __name__ == '__main__':
	moveTower(3, "A", "B", "C")

运行结果如下

Move disk 1 form A to C
Move disk 2 form A to B
Move disk 1 form C to B
Move disk 3 form A to C
Move disk 1 form B to A
Move disk 2 form B to C
Move disk 1 form A to C

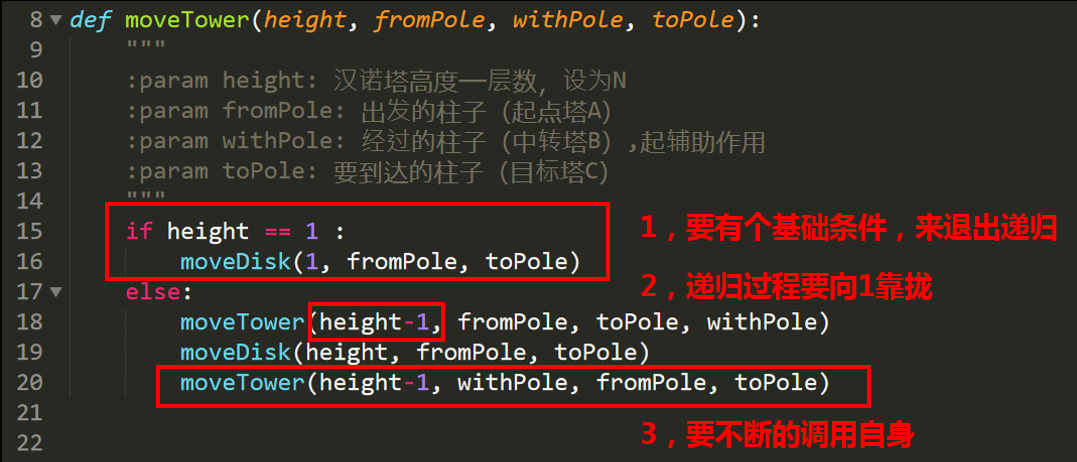
然后我们结合代码回顾一下递归三原则
如图所示：
在这里插入图片描述

3、可视化实现

要实现可视化，则
1要绘制两个形状：塔，圆盘
2要移动绘制后的形状
代码实现思路为：
先定义塔、圆盘对应的形状画笔，在通过移动画笔实现形状的移动
最终代码如下

import turtle
 
# ==============
#  常量设置
# ==============
N=3 # 汉诺塔层数限制
 
BasePL=12   # plate的大小基数，修改这个能够调整plate的大小
TowerP=5    # Tower的线宽
TowerW=110  # Tower的底座宽度
TowerH=200  # Tower的高度
TowerSpace=260  # Tower的之间的距离，从中心到中心
HORIZON=-100    # Tower的底座高度，用于定位
# 动画速度，5是比较适中的速度
PMS=1
 
# 优化处理
Isjump=True
 
POLES={
    "1": [],
    "2": [],
    "3": [],
}
PLATES=[] # 存储所有圆盘对象
 
# 塔的颜色
LineColor="black"
# 多个盘子的颜色
FillColors=[
    "#d25b6a",
    "#d2835b",
    "#e5e234",
    "#83d05d",
    "#2862d2",
    "#35b1c0",
    "#5835c0"
]
# 建立窗体
SCR=turtle.Screen()
# SCR.tracer()
SCR.setup(800,600) #设置窗体大小
 
 
# 设置圆盘形状
def set_plate(pi=0):
    _pi=pi+2
    t = turtle.Turtle()
    t.hideturtle()
    t.speed(0)
    t.penup()
    t.begin_poly()
    t.left(90)
    t.forward(BasePL*_pi)
    t.circle(BasePL, 180)
    t.forward(BasePL * 2 * _pi)
    t.circle(BasePL, 180)
    t.forward(BasePL * _pi)
    t.end_poly()
    p = t.get_poly()
    pname='plate_%s'%pi
    SCR.register_shape(pname, p)
 
 
# 设置塔柱形状
def set_tower():
    t = turtle.Turtle()
    t.hideturtle()
    t.speed(0)
    t.penup()
 
    t.begin_poly()
    t.left(90)
    t.forward(TowerW)
    t.circle(-TowerP, 180)
    t.forward(TowerW)
    t.forward(TowerW)
    t.circle(-TowerP, 180)
    t.forward(TowerW-TowerP/2)
 
    t.left(90)
    t.forward(TowerH)
    t.circle(-TowerP, 180)
    t.forward(TowerH)
    t.end_poly()
    p = t.get_poly()
    SCR.register_shape('tower', p)
 
 
# 绘制塔柱
def draw_towers():
    set_tower()
    for tx in [-TowerSpace,0,TowerSpace]:
        t3 = turtle.Turtle('tower')
        t3.penup()
        t3.goto(tx,HORIZON)
 
 
# 绘制圆盘
def draw_plates(pn=4):
    plates=[]
    for i in range(pn):
        set_plate(i)
        _plate='plate_%s'%i
        _p=turtle.Turtle(_plate)
        _colorIdx = i % len(FillColors)
        _color=FillColors[_colorIdx]
 
        _p.color(_color,_color)
        _p.speed(PMS)
        plates.append(_p)
    # 反序，大的在前，小的在后
    global PLATES
    PLATES = plates[:]
 
# 绘制移动过程
def draw_move(diskIndex, fromPindex, toPindex):
    p=PLATES[diskIndex-1]
    index_loc={
        "A":1,
        "B":2,
        "C":3
    }
    toP=index_loc.get(toPindex,None)
    fromP=index_loc.get(fromPindex,None)
 
    p.penup()
 
    mx = (toP - 2) * TowerSpace
    my = HORIZON + len(POLES[str(toP)]) * BasePL * 2
 
    if fromP!=None:
        POLES[str(fromP)].remove(p)
        if Isjump:
            px,py=p.pos()
            p.goto(px,TowerH+py)
            p.goto(mx,TowerH+py)
 
    p.goto(mx, my)
    POLES[str(toP)].append(p)
 
 
# 将所有圆盘移动到起点
def movetoA(n,fromPindex):
    for i in range(n,0,-1):
        draw_move(i,None,fromPindex)
 
 
# 移动指定层圆盘diskIndex，从fromPole出发，到达toPole
def moveDisk(diskIndex,fromPole,toPole):
    """
    :param diskIndex: 圆盘的索引（从上往下，第一层为1，第二层为2、、、第n层为n）
    :param fromPole: 出发的柱子（起点）
    :param toPole: 要到达的柱子（终点）
    :return:
    """
    draw_move(diskIndex, fromPole, toPole)
 
 
# 核心函数，入口
def moveTower(height,fromPole, withPole, toPole):
    """
    :param height: 汉诺塔高度——层数
    :param fromPole: 出发的柱子（起点）
    :param withPole: 进过的柱子（中转点）
    :param toPole: 要到达的柱子（终点）
    :return:
    """
    if height == 1:
        # 基础情形：一层的汉诺塔
        moveDisk(1,fromPole, toPole)
        return
 
    # 先将圆盘1到n - 1看作一个整体从起点塔移动到中转塔（用目标塔作为本步骤的中转）
    moveTower(height-1,fromPole,toPole,withPole)
    # 再将圆盘n从起点塔A移动到目标塔C
    moveDisk(height,fromPole,toPole)
    # 最后将圆盘1到n - 1看作一个整体从中转塔移动到目标塔（用起点塔作为本步骤的中转）
    moveTower(height-1,withPole,fromPole,toPole)
 
 
if __name__ == '__main__':
    # 调用
    # 三层汉诺塔，A为出发柱子，B为中转柱子，C为目标柱子
    n=N
     
    SCR.tracer(0)
    draw_towers()
    draw_plates(n)
    movetoA(n,"A")
    SCR.tracer(1)

    moveTower(n,"A","B","C")
    turtle.done()

点击观看代码对应移动动画

本文主要通过三个实例来帮助大家理解递归（其展示动画已上传B站）：
谢尔宾斯基三角形(Sierpinski Triangle)
汉诺塔(Tower of Hanoi)
迷宫探索(Maze Exploring)
本文代码已上传到github：https://github.com/BigShuang/recursion-with-turtle
本文参考文献：
Problem Solving with Algorithms and Data Structures using Python
turtle官方文档：
中文：https://docs.python.org/zh-cn/3.6/library/turtle.html
英文：https://docs.python.org/3.6/library/turtle.html