Tightly Coupled LiDAR Inertial Odometry and Mapping源码解析(二)
3. Joint optimization
在上一个博客中,我们分别介绍了IMU预积分,LiDAR Relative Measurements,接下来就是非常重要优化环节了,优化过后才可以获得里程计计算结果。在这篇论文中,优化的目标函数主要由三部分构成:marginalization factor, imu-preintegration,以及LiDAR relative measurements,我们首先来看第一个marginalization factor。
3.1 Marginalization
3.1.1 什么是Marginalization
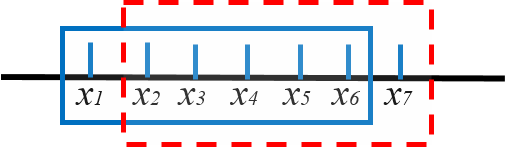
在上一博客中,我们已经知道该篇论文中引入了一个滑窗(Sliding Window),来限制待优化的状态向量数量。如下图所示,我们考虑这样一种情景,假设当前时刻窗口内的优化变量为
x
1
,
x
2
,
.
.
.
,
x
6
x_1,x_2,...,x_6
x1,x2,...,x6,且已经对里程计中的目标函数完成了优化,也就是相当于拟合出来了一个概率分布
p
(
x
1
,
x
2
,
.
.
.
,
x
6
)
p(x_1,x_2,...,x_6)
p(x1,x2,...,x6),即多维高斯分布对应的均值
μ
\mu
μ和协方差矩阵
K
K
K。此时在下一个优化时刻到来之前,我们需要将窗口往后移动一个格子,即开始优化此时窗口内的优化变量
x
2
,
x
3
,
.
.
.
,
x
7
x_2,x_3,...,x_7
x2,x3,...,x7,这种过程会贯穿整个估计过程,直至算法停止运行。那么一个明显的问题是,我们在优化拟合出来
p
(
x
2
,
x
3
,
.
.
.
,
x
7
)
p(x_2,x_3,...,x_7)
p(x2,x3,...,x7)之前,该怎样处理概率分布
p
(
x
1
,
x
2
,
.
.
.
,
x
6
)
p(x_1,x_2,...,x_6)
p(x1,x2,...,x6)呢?
为了更形象的说明这个问题,我们来假设这样一种情景。小明开车想从中国科学技术大学到之心城买件衣服,怕迷路,想时刻估计一下自己到哪了,因此搞了个滑窗,利用gps,轮速计来分析自己当前和过往几个时刻自己开车到哪了。通过各种融合算法,发现自己
x
1
,
x
2
,
.
.
.
,
x
6
x_1,x_2,...,x_6
x1,x2,...,x6时的位置分布为
p
(
x
1
,
x
2
,
.
.
.
,
x
6
)
p(x_1,x_2,...,x_6)
p(x1,x2,...,x6)发现自己原来刚出东门。然后接着往前开啊,现在滑窗内的状态就是
x
2
,
x
3
,
.
.
.
,
x
7
x_2,x_3,...,x_7
x2,x3,...,x7了。那么如何估计我
x
2
,
x
3
,
.
.
.
,
x
7
x_2,x_3,...,x_7
x2,x3,...,x7时刻的位置呢?
一种方法就是继续像上一时刻那样用自身的gps和轮速计等融合
p
(
x
2
,
x
3
,
.
.
.
,
x
7
)
p(x_2,x_3,...,x_7)
p(x2,x3,...,x7),也就是说我才不管你
x
1
,
x
2
,
x
3
,
.
.
.
,
x
6
x_1,x_2,x_3,...,x_6
x1,x2,x3,...,x6时在哪,我只关心
p
(
x
2
,
x
3
,
.
.
.
,
x
7
)
p(x_2,x_3,...,x_7)
p(x2,x3,...,x7),计算完发现我去怎么还在东门附近?不是刚路过了吗?是不是算错了?
这时,聪明的副驾驶提醒你,哎这孩子读书读傻了,笨不笨,明明
(
x
1
,
x
2
,
.
.
.
,
x
6
)
(x_1,x_2,...,x_6)
(x1,x2,...,x6)时刻都到
p
(
x
1
,
x
2
,
.
.
.
,
x
6
)
p(x_1,x_2,...,x_6)
p(x1,x2,...,x6)了,你咋还给忘了?你这不是黑瞎子掰玉米掰一个扔一个吗?把
p
(
x
2
,
.
.
.
,
x
6
)
p(x_2,...,x_6)
p(x2,...,x6)也就是我们刚刚路过东门这个消息加到你的那个什么融合算法里,再算一算我们现在到哪了?小明这才计算出来原来已经到东门前的十字路口了。
这个例子说明,在更新计算
p
(
x
2
,
x
3
,
.
.
.
,
x
7
)
p(x_2,x_3,...,x_7)
p(x2,x3,...,x7)时,总共有两种方法,第一种是直接丢掉之前窗口内拟合的分布
p
(
x
1
,
x
2
,
.
.
.
,
x
6
)
p(x_1,x_2,...,x_6)
p(x1,x2,...,x6),重新计算估计
p
(
x
2
,
x
3
,
.
.
.
,
x
7
)
p(x_2,x_3,...,x_7)
p(x2,x3,...,x7)。但是这种方法有一个比较重要的缺陷就是信息损失,可能
p
(
x
2
,
x
3
,
.
.
.
,
x
6
)
p(x_2,x_3,...,x_6)
p(x2,x3,...,x6)内的估计非常准确,而你却把这么重要的信息给直接扔了,这不是败家吗你说?第二种方法就是将
p
(
x
1
,
x
2
,
.
.
.
,
x
6
)
p(x_1,x_2,...,x_6)
p(x1,x2,...,x6)中的
p
(
x
2
,
x
3
,
.
.
.
,
x
6
)
p(x_2,x_3,...,x_6)
p(x2,x3,...,x6)计算出来,并将
p
(
x
2
,
x
3
,
.
.
.
,
x
6
)
p(x_2,x_3,...,x_6)
p(x2,x3,...,x6)作为先验信息加入到新窗口的估计中。那么问题来了,怎样根据
p
(
x
1
,
x
2
,
.
.
.
,
x
6
)
p(x_1,x_2,...,x_6)
p(x1,x2,...,x6)计算
p
(
x
2
,
x
3
,
.
.
.
,
x
6
)
p(x_2,x_3,...,x_6)
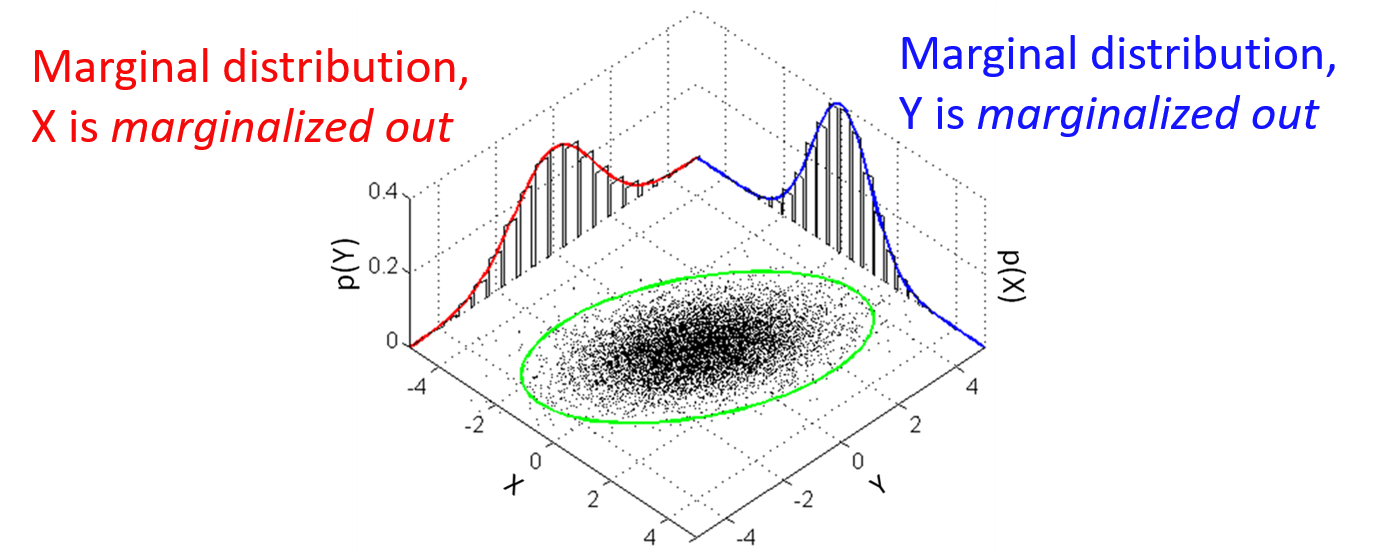
p(x2,x3,...,x6)呢?这个过程就叫做Marginalization。下图能比较清晰严谨的说明这个问题,数理基础比较好的话也能想到我们好像学过这个公式:
p
(
x
a
)
=
∫
x
b
p
(
x
a
,
x
b
)
p(x_a)=\int_{x_b}p(x_a,x_b)
p(xa)=∫xbp(xa,xb)。接下来我们从数学的角度严谨的说明一下Marginalization。
3.1.2 Basics of Multi-variate Gauss Distribution
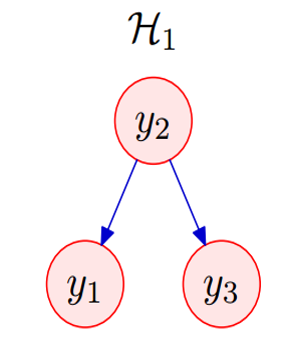
如下图所示,假设有一个系统长这个样子,其中
y
2
y_2
y2表示的是室外的温度,
y
1
y_1
y1表示的是房间1的温度,
y
3
y_3
y3表示的是房间3的温度,且他们之间的函数关系表示为:
{
y
2
=
v
2
y
1
=
w
1
y
2
+
v
1
y
3
=
w
3
y
2
+
v
3
v
i
−
N
(
0
,
σ
i
2
)
,
高
斯
噪
声
\begin{cases} y_2=v_2\\ y_1=w_1y_2+v_1\\ y_3=w_3y_2+v_3\\ v_i-N(0,\sigma_i^2),高斯噪声 \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧y2=v2y1=w1y2+v1y3=w3y2+v3vi−N(0,σi2),高斯噪声
则状态向量
y
=
[
y
1
,
y
2
,
y
3
]
T
y=[y_1,y_2,y_3]^T
y=[y1,y2,y3]T对应的协防差矩阵
K
K
K为:
K
11
=
E
(
y
1
y
1
)
=
w
1
2
σ
2
2
+
σ
1
2
,
K
22
=
E
(
y
2
y
2
)
=
σ
2
2
,
K
33
=
E
(
y
3
y
3
)
=
w
3
2
σ
2
2
+
σ
3
2
K
12
=
K
21
=
E
(
y
1
y
2
)
=
w
1
2
σ
2
2
,
K
13
=
K
31
=
w
1
w
3
σ
2
2
,
K
23
=
K
32
=
w
3
σ
2
2
K_{11}=E(y_1y_1)=w_1^2\sigma_2^2+\sigma_1^2,K_{22}=E(y_2y_2)=\sigma_2^2,K_{33}=E(y_3y_3)=w_3^2\sigma_2^2+\sigma_3^2 \\ K_{12}=K_{21}=E(y_1y_2)=w_1^2\sigma_2^2,K_{13}=K_{31}=w_1w_3\sigma_2^2,K_{23}=K_{32}=w_3\sigma_2^2
K11=E(y1y1)=w12σ22+σ12,K22=E(y2y2)=σ22,K33=E(y3y3)=w32σ22+σ32K12=K21=E(y1y2)=w12σ22,K13=K31=w1w3σ22,K23=K32=w3σ22
即:
K
=
(
w
1
2
σ
2
2
+
σ
1
2
w
1
σ
2
2
w
1
w
3
σ
2
2
w
1
σ
2
2
σ
2
2
w
3
σ
2
2
w
1
w
3
σ
2
2
w
3
σ
2
2
w
3
2
σ
2
2
+
σ
3
2
)
K= \left( \begin{matrix} w_1^2\sigma_2^2+\sigma_1^2 & w_1\sigma_2^2 & w_1w_3\sigma_2^2\\ w_1\sigma_2^2 & \sigma_2^2 & w_3\sigma_2^2\\ w_1w_3\sigma_2^2 & w_3\sigma_2^2 & w_3^2\sigma_2^2+\sigma_3^2 \end{matrix} \right)
K=⎝⎛w12σ22+σ12w1σ22w1w3σ22w1σ22σ22w3σ22w1w3σ22w3σ22w32σ22+σ32⎠⎞
现在知道了该向量对应的协方差矩阵,只需要求解其逆矩阵就可以得到信息矩阵。不过直接求解其逆矩阵还是比较麻烦的,因此我们按照如下的方法求解。我们首先需要求解对应的联合概率分布,则根据贝叶斯公式可以得到:
p
(
y
1
,
y
2
,
y
3
)
=
p
(
y
1
,
y
3
∣
y
2
)
p
(
y
2
)
=
p
(
y
1
∣
y
3
,
y
2
)
p
(
y
3
∣
y
2
)
p
(
y
2
)
p(y_1,y_2,y_3)=p(y_1,y_3|y_2)p(y_2)=p(y_1|y_3,y_2)p(y_3|y_2)p(y_2)
p(y1,y2,y3)=p(y1,y3∣y2)p(y2)=p(y1∣y3,y2)p(y3∣y2)p(y2)
而由前面之间的关系我们知道,
y
1
y_1
y1是不依赖于
y
3
y_3
y3的,因此
p
(
y
1
∣
y
3
,
y
2
)
=
p
(
y
1
∣
y
2
)
p(y_1|y_3,y_2)=p(y_1|y_2)
p(y1∣y3,y2)=p(y1∣y2),因此上式可以化简为:
p
(
y
1
,
y
2
,
y
3
)
=
p
(
y
1
∣
y
2
)
p
(
y
3
∣
y
2
)
p
(
y
2
)
p(y_1,y_2,y_3)=p(y_1|y_2)p(y_3|y_2)p(y_2)
p(y1,y2,y3)=p(y1∣y2)p(y3∣y2)p(y2)
p
(
y
2
)
=
1
Z
2
e
−
y
2
2
2
σ
2
2
p(y_2)=\frac{1}{Z_2}e^{-\frac{y_2^2}{2\sigma_2^2}}
p(y2)=Z21e−2σ22y22
p
(
y
1
∣
y
2
)
=
1
Z
1
e
−
(
y
1
−
w
1
y
2
)
2
2
σ
1
2
p(y_1|y_2)=\frac{1}{Z_1}e^{-\frac{(y_1-w_1y_2)^2}{2\sigma_1^2}}
p(y1∣y2)=Z11e−2σ12(y1−w1y2)2
p
(
y
3
∣
y
2
)
=
1
Z
3
e
−
(
y
3
−
w
3
y
2
)
2
2
σ
3
2
p(y_3|y_2)=\frac{1}{Z_3}e^{-\frac{(y_3-w_3y_2)^2}{2\sigma_3^2}}
p(y3∣y2)=Z31e−2σ32(y3−w3y2)2
p
(
y
1
,
y
2
,
y
3
)
=
1
Z
′
e
x
p
(
−
1
2
(
y
2
2
σ
2
2
+
(
y
1
−
w
1
y
2
)
2
σ
1
2
+
(
y
3
−
w
3
y
2
)
2
σ
3
2
)
)
p(y_1,y_2,y_3)=\frac{1}{Z'}exp(-\frac{1}{2}(\frac{y_2^2}{\sigma_2^2}+\frac{(y_1-w_1y_2)^2}{\sigma_1^2}+\frac{(y_3-w_3y_2)^2}{\sigma_3^2}))
p(y1,y2,y3)=Z′1exp(−21(σ22y22+σ12(y1−w1y2)2+σ32(y3−w3y2)2))
写成信息矩阵的形式既可以写为:
p
(
y
1
,
y
2
,
y
3
)
=
1
Z
′
e
x
p
(
−
1
2
[
y
1
y
2
y
3
]
[
1
σ
1
2
−
w
1
σ
1
2
0
−
w
1
σ
1
2
1
σ
2
2
+
w
1
2
σ
1
2
+
w
3
2
σ
3
2
−
w
3
σ
3
2
0
−
w
3
σ
3
2
1
σ
3
2
]
[
y
1
y
2
y
3
]
)
p(y_1,y_2,y_3)=\frac{1}{Z'}exp(-\frac{1}{2}\left[\begin{matrix}y_1 & y_2 & y_3\end{matrix}\right]\left[\begin{matrix}\frac{1}{\sigma_1^2} & -\frac{w_1}{\sigma_1^2} & 0\\-\frac{w_1}{\sigma_1^2} & \frac{1}{\sigma_2^2}+\frac{w_1^2}{\sigma_1^2}+\frac{w_3^2}{\sigma_3^2} & -\frac{w_3}{\sigma_3^2}\\0 & -\frac{w_3}{\sigma_3^2} & \frac{1}{\sigma_3^2}\end{matrix}\right]\left[\begin{matrix}y_1 \\ y_2\\ y_3\end{matrix}\right])
p(y1,y2,y3)=Z′1exp(−21[y1y2y3]⎣⎢⎡σ121−σ12w10−σ12w1σ221+σ12w12+σ32w32−σ32w30−σ32w3σ321⎦⎥⎤⎣⎡y1y2y3⎦⎤)
Ω
=
[
1
σ
1
2
−
w
1
σ
1
2
0
−
w
1
σ
1
2
1
σ
2
2
+
w
1
2
σ
1
2
+
w
3
2
σ
3
2
−
w
3
σ
3
2
0
−
w
3
σ
3
2
1
σ
3
2
]
\Omega=\left[\begin{matrix}\frac{1}{\sigma_1^2} & -\frac{w_1}{\sigma_1^2} & 0\\-\frac{w_1}{\sigma_1^2} & \frac{1}{\sigma_2^2}+\frac{w_1^2}{\sigma_1^2}+\frac{w_3^2}{\sigma_3^2} & -\frac{w_3}{\sigma_3^2}\\0 & -\frac{w_3}{\sigma_3^2} & \frac{1}{\sigma_3^2}\end{matrix}\right]
Ω=⎣⎢⎡σ121−σ12w10−σ12w1σ221+σ12w12+σ32w32−σ32w30−σ32w3σ321⎦⎥⎤
3.1.3 Marginalization in covariance and information form
对于3.1.2中的系统,现在我们想marginalize out状态变量
y
3
y_3
y3,也就是说现在的状态向量变为
y
‘
=
[
y
1
,
y
2
]
T
y‘=[y_1,y_2]^T
y‘=[y1,y2]T,则该状态向量对应的协方差矩阵为:
K
′
=
[
w
1
2
σ
2
2
+
σ
1
2
w
1
σ
2
2
w
1
σ
2
2
σ
2
2
]
K'=\left[ \begin{matrix} w_1^2\sigma_2^2+\sigma_1^2 & w_1\sigma_2^2\\ w_1\sigma_2^2 & \sigma_2^2 \end{matrix} \right]
K′=[w12σ22+σ12w1σ22w1σ22σ22]
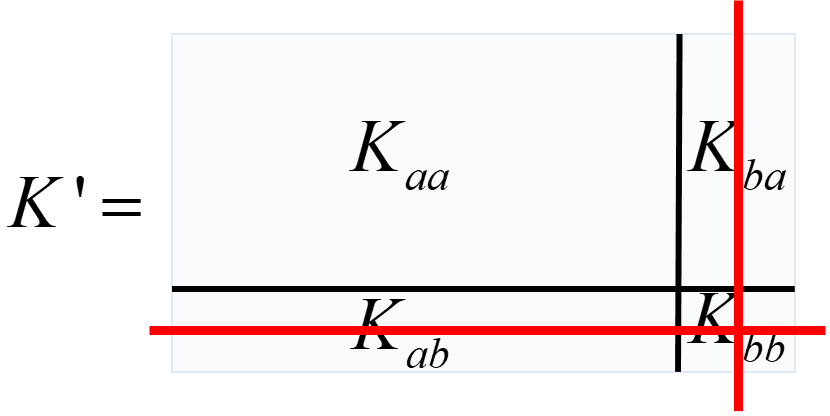
从
K
′
K'
K′和
K
K
K的对比中我们可以发现,在marginalize out
y
3
y_3
y3后,新的状态变量对应的协方差矩阵
K
′
K'
K′不过是将原来的协方差矩阵
K
K
K的第3行和第3列删掉,那么信息矩阵是不是也是这样呢?我们一起来推导一下。
p
(
y
1
,
y
2
)
=
p
(
y
1
∣
y
2
)
p
(
y
2
)
=
1
Z
′
e
x
p
(
−
1
2
(
y
2
2
σ
2
2
+
(
y
1
−
w
1
y
2
)
2
σ
1
2
)
)
=
1
Z
′
e
x
p
(
−
1
2
[
y
1
y
2
]
[
1
σ
1
2
−
w
1
σ
1
2
−
w
1
σ
1
2
1
σ
2
2
+
w
1
2
σ
1
2
]
[
y
1
y
2
]
)
p(y_1,y_2)=p(y_1|y_2)p(y_2)=\frac{1}{Z'}exp(-\frac{1}{2}(\frac{y_2^2}{\sigma_2^2}+\frac{(y_1-w_1y_2)^2}{\sigma_1^2}))\\=\frac{1}{Z'}exp(-\frac{1}{2}\left[ \begin{matrix}y_1 & y_2\end{matrix} \right]\left[ \begin{matrix} \frac{1}{\sigma_1^2} & -\frac{w_1}{\sigma_1^2}\\ -\frac{w_1}{\sigma_1^2} & \frac{1}{\sigma_2^2}+\frac{w_1^2}{\sigma_1^2} \end{matrix} \right]\left[ \begin{matrix}y_1 \\ y_2\end{matrix} \right])
p(y1,y2)=p(y1∣y2)p(y2)=Z′1exp(−21(σ22y22+σ12(y1−w1y2)2))=Z′1exp(−21[y1y2][σ121−σ12w1−σ12w1σ221+σ12w12][y1y2])
也就是说:
Ω
′
=
[
1
σ
1
2
−
w
1
σ
1
2
−
w
1
σ
1
2
1
σ
2
2
+
w
1
2
σ
1
2
]
\Omega'=\left[ \begin{matrix} \frac{1}{\sigma_1^2} & -\frac{w_1}{\sigma_1^2}\\ -\frac{w_1}{\sigma_1^2} & \frac{1}{\sigma_2^2}+\frac{w_1^2}{\sigma_1^2} \end{matrix} \right]
Ω′=[σ121−σ12w1−σ12w1σ221+σ12w12]
发现,咦,信息矩阵好像不像协方差矩阵那样直接把
y
3
y_3
y3对应的第3行和第3列去掉就可以了。也就是说对于一般情况来讲,假如一个状态向量为
x
=
[
a
T
,
b
T
]
T
x=[a^T,b^T]^T
x=[aT,bT]T,如果我们想marginalize out状态向量
b
b
b,那么对于协方差矩阵仅需要将状态向量
b
b
b对应的行和列删除就可以。可是信息矩阵不行啊,这怎么办呢?这时候就需要Schur Complement了。skir~~ skir~~
3.1.4 Schur Complement
为不失一般性,咱这次就不拿前两节中那个温度模型说事儿了。现在假设状态变量为
x
=
[
a
T
,
b
T
]
T
x=[a^T,b^T]^T
x=[aT,bT]T,其对应的协防差矩阵为:
K
=
[
A
C
T
C
D
]
K=\left[ \begin{matrix} A & C^T\\ C & D \end{matrix} \right]
K=[ACCTD]
其中,
A
A
A和
D
D
D为可逆方阵。
记其信息矩阵为
Λ
\Lambda
Λ:
Λ
=
[
Λ
a
a
Λ
a
b
Λ
b
a
Λ
b
b
]
\Lambda = \left[ \begin{matrix} \Lambda_{aa} & \Lambda_{ab}\\ \Lambda_{ba} & \Lambda_{bb} \end{matrix} \right]
Λ=[ΛaaΛbaΛabΛbb]
假设状态变量
x
x
x满足多维高斯分布,则有下式:
p
(
x
)
=
p
0
e
x
p
(
−
1
2
E
)
p(x)=p_0exp(-\frac{1}{2}E)
p(x)=p0exp(−21E)
E
=
[
x
a
T
,
x
b
T
]
Λ
[
x
a
x
b
]
=
[
x
a
T
,
x
b
T
]
[
Λ
a
a
Λ
a
b
Λ
b
a
Λ
b
b
]
[
x
a
x
b
]
\begin{matrix} E =\left[x_a^T,x_b^T\right]\Lambda\left[\begin{matrix}x_a\\x_b\end{matrix}\right]\\ = \left[x_a^T,x_b^T\right]\left[\begin{matrix}\Lambda_{aa}&\Lambda_{ab}\\\Lambda_{ba}&\Lambda_{bb}\end{matrix}\right]\left[\begin{matrix}x_a\\x_b\end{matrix}\right] \end{matrix}
E=[xaT,xbT]Λ[xaxb]=[xaT,xbT][ΛaaΛbaΛabΛbb][xaxb]
将上式打开就可以得到下式:
E
=
x
a
T
Λ
a
a
x
a
+
2
x
b
T
Λ
b
a
x
a
+
x
b
T
Λ
b
b
x
b
E=x_a^T\Lambda_{aa}x_a+2x_b^T\Lambda_{ba}x_a+x_b^T\Lambda_{bb}x_b
E=xaTΛaaxa+2xbTΛbaxa+xbTΛbbxb
容易发现上式就是一个二次型,比较遗憾的是存在一个
x
b
x_b
xb和
x
a
x_a
xa的交叉项。为了分离变量,就需要用到我们线性代数中学过的配方法求标准二次型问题了。考虑到这个东西可能离大家比较久远,我们首先来简单回顾一下这种方法,简单来说就比如说一个函数
Q
(
x
1
,
x
2
)
=
x
1
2
+
x
2
2
+
3
x
1
x
2
Q(x_1,x_2)=x_1^2+x_2^2+3x_1x_2
Q(x1,x2)=x12+x22+3x1x2,写成矩阵的形式就是:
Q
(
x
1
,
x
2
)
=
[
x
1
,
x
2
]
[
1
3
0
1
]
[
x
1
x
2
]
Q(x_1,x_2)=\left[x_1,x_2\right]\left[\begin{matrix}1&3\\0&1\end{matrix}\right]\left[\begin{matrix}x_1\\x_2\end{matrix}\right]
Q(x1,x2)=[x1,x2][1031][x1x2]
我们说这个东西不是标准二次型就是因为中间的矩阵不是对角阵,右上角有一个比较烦人的数字3.那么怎么能把这个3搞没呢,这里就可以无脑用配方法啦。可以把Q函数改写成:
Q
(
x
1
,
x
2
)
=
(
x
1
+
3
2
x
2
)
2
−
5
4
x
2
2
Q(x_1,x_2)=(x_1+\frac{3}{2}x_2)^2-\frac{5}{4}x_2^2
Q(x1,x2)=(x1+23x2)2−45x22
如果另
y
1
=
x
1
+
1.5
×
x
2
,
y
2
=
x
2
y_1=x_1+1.5\times x_2,y_2=x_2
y1=x1+1.5×x2,y2=x2,然后上式就可以改写成:
Q
(
y
1
,
y
2
)
=
y
1
2
−
1.25
y
2
2
Q(y_1,y_2)=y_1^2-1.25y_2^2
Q(y1,y2)=y12−1.25y22,也就是标准二次型的形式。
按照这种方法我们对
E
E
E进行标准化则可以得到:
E
=
(
x
b
+
Λ
b
b
−
1
Λ
b
a
x
a
)
T
Λ
b
b
(
x
b
+
Λ
b
b
−
1
Λ
b
a
x
a
)
+
x
a
T
(
Λ
a
a
−
Λ
b
a
T
Λ
b
b
−
1
Λ
b
a
)
x
a
E=(x_b+\Lambda_{bb}^{-1}\Lambda_{ba}x_a)^T\Lambda_{bb}(x_b+\Lambda_{bb}^{-1}\Lambda_{ba}x_a)+x_a^T(\Lambda_{aa}-\Lambda_{ba}^T\Lambda_{bb}^{-1}\Lambda_{ba})x_a
E=(xb+Λbb−1Λbaxa)TΛbb(xb+Λbb−1Λbaxa)+xaT(Λaa−ΛbaTΛbb−1Λba)xa
所谓的
Λ
a
a
−
Λ
b
a
T
Λ
b
b
−
1
Λ
b
a
\Lambda_{aa}-\Lambda_{ba}^T\Lambda_{bb}^{-1}\Lambda_{ba}
Λaa−ΛbaTΛbb−1Λba,也就是我们经常在论文里面看到的Schur Complements了,将会给基于信心矩阵的边缘化带来极大方便。对化简后的概率分布求积分
p
(
x
a
)
=
∫
p
(
x
a
,
x
b
)
d
x
b
p(x_a)=\int p(x_a,x_b)dx_b
p(xa)=∫p(xa,xb)dxb就可以得到去掉
x
b
x_b
xb后的边缘分布啦,其信息矩阵就是这个schur complement。关于这部分的详细推导建议大家看这篇论文里面的定理1:
Manipulating the Multivariate Gaussian Density。
好了这篇博客就先到这里了,我们下篇博客见。