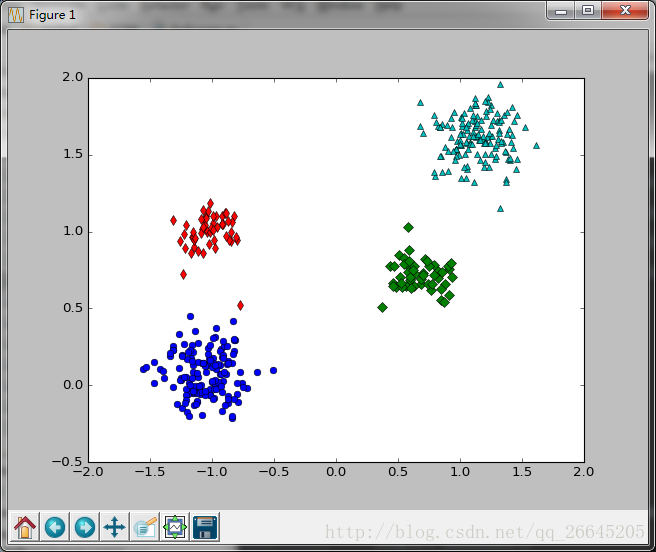
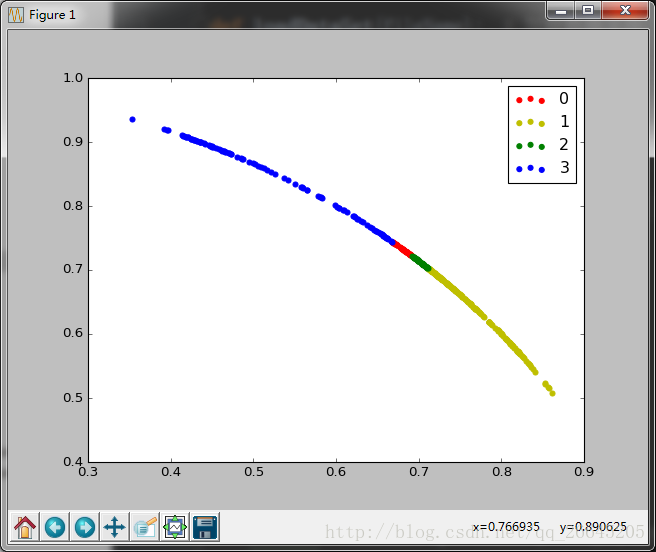
下面为两种SOM的运行代码,用来分类同样的数据,第一种学习率和聚类半径随着迭代次数的变化而变化,参考机器学习之自组织特征映射神经网络(SOM),同时运行博客点这里的代码,比较运行时间,都设置迭代次数为1000次,分4类,运行时间分为为0(即小于1s)和17s。
两种方式的归一化方法不一样。一个是维度归一化,一个是一般的归一化(行向量)
代码1
from numpy import *
import matplotlib.pyplot as plt
import string
class Kohonen(object):
def __init__(self):
self.lratemax=0.8 #最大学习率-欧式距离
self.lratemin=0.05 #最小学习率-欧式距离
self.rmax=5 #最大聚类半径--根据数据集
self.rmin=0.5 #最小聚类半径--根据数据集
self.Steps=1000 #迭代次数
self.lratelist=[] #学习率收敛曲线
self.rlist=[] #学习率半径曲线
self.w=[] #权重向量组
self.M=2 # M*N表示聚类总数
self.N=2 #M、N表示邻域的参数
self.dataMat=[] #外部导入数据集
self.classLabel=[] #聚类后的类别标签
def loadDate(self,fileName): #加载数据文件
fr=open(fileName)
for line in fr.readlines():
curLine=line.strip().split("\t")
lineArr=[]
lineArr.append(float(curLine[0]))
lineArr.append(float(curLine[1]))
self.dataMat.append(lineArr)
self.dataMat=mat(self.dataMat)
def file2matrix(self,path, delimiter):
recordlist = []
fp = open(path)
content = fp.read()
fp.close()
rowlist = content.splitlines() # 按行转换为一维表
# 逐行遍历 # 结果按分隔符分割为行向量
recordlist = [map(eval, row.split(delimiter)) for row in rowlist if row.strip()]
# 返回转换后的矩阵形式
self.dataMat = mat(recordlist)
def normalize(self,dataMat):
[m,n]=shape(dataMat)
for i in xrange(n):
dataMat[:,i] =(dataMat[:,i]-mean(dataMat[:,]))/std(dataMat[:,])
return dataMat
def distEclud(self,matA,matB):
ma, na = shape(matA);
mb, nb = shape(matB);
rtnmat = zeros((ma, nb))
for i in xrange(ma):
for j in xrange(nb):
rtnmat[i, j] = linalg.norm(matA[i, :] - matB[:, j].T)
return rtnmat
def init_grid(self): #初始化第二层网格
[m, n] = shape(self.dataMat)
k=0 #构建低二层网络模型
#数据集的维度即网格的维度,分类的个数即网格的行数
grid=mat(zeros((self.M*self.N,n)))
for i in xrange(self.M):
for j in xrange(self.N):
grid[k,:]=[i,j]
k+=1
return grid
def ratecalc(self,i):
lrate = self.lratemax - (i + 1.0) * (self.lratemax - self.lratemin) / self.Steps
r = self.rmax - ((i + 1.0) * (self.rmax - self.rmin)) / self.Steps
return lrate,r
#主程序
def train(self):
#1.构建输入层网络
dm,dn=shape(self.dataMat)
#归一化数据
normDataSet=self.normalize(self.dataMat)
#2.初始化第二层分类网络
grid=self.init_grid()
#3.随机初始化两层之间的权重向量
self.w=random.rand(dn,self.M*self.N)
distM=self.distEclud #确定距离公式
#4.迭代求解
if self.Steps<5*dm:self.Steps=5*dm #设定最小迭代次数
for i in xrange(self.Steps):
lrate,r=self.ratecalc(i) #1.计算当前迭代次数下的学习率和学习聚类半径
self.lratelist.append(lrate);self.rlist.append(r)
#2.随机生成样本索引,并抽取一个样本
k=random.randint(0,dm)
mySample=normDataSet[k,:]
#3.计算最优节点:返回最小距离的索引值
minIndx=(distM(mySample,self.w)).argmin()
#4.计算领域
d1=ceil(minIndx/self.M) #计算此节点在第二层矩阵中的位置
d2=mod(minIndx,self.M)
distMat=distM(mat([d1,d2]),grid.T)
nodelindx=(distMat<r).nonzero()[1] #获取领域内的所有点
for j in xrange(shape(self.w)[1]):
if sum(nodelindx==j):
self.w[:,j]=self.w[:,j]+lrate*(mySample[0]-self.w[:,j])
#主循环结束
self.classLabel=range(dm) #分配和存储聚类后的类别标签
for i in xrange(dm):
self.classLabel[i]=distM(normDataSet[i,:],self.w).argmin()
self.classLabel=mat(self.classLabel)
def showCluster(self,plt): #绘图
lst=unique(self.classLabel.tolist()[0]) #去重
i=0
for cindx in lst:
myclass = nonzero(self.classLabel==cindx)[1]
xx=self.dataMat[myclass].copy()
if i==0: plt.plot(xx[:,0],xx[:,1],'bo')
elif i==1:plt.plot(xx[:,0],xx[:,1],'rd')
elif i==2:plt.plot(xx[:,0],xx[:,1],'gD')
elif i==3:plt.plot(xx[:,0],xx[:,1],'c^')
i+=1
plt.show()
if __name__=="__main__":
SOMNet=Kohonen()
SOMNet.loadDate('dataset2.txt')
SOMNet.train()
SOMNet.showCluster(plt)
代码2
参考:http://blog.csdn.net/chenge_j/article/details/72537568
from numpy import *
import matplotlib.pyplot as plt
from numpy import linalg
#初始化输入层与竞争层神经元的连接权值矩阵
def initCompetition(n , m , d):
#随机产生0-1之间的数作为权值
array = random.random(size=n * m *d)
com_weight = array.reshape(n,m,d)
return com_weight
#计算向量的二范数
def cal2NF(X):
res = 0
# return linalg.norm(X)
for x in X:
res += x*x
return res ** 0.5
#对数据集进行归一化处理
def normalize(dataSet):
old_dataSet = copy(dataSet)
for data in dataSet:
two_NF = cal2NF(data)
for i in range(len(data)):
data[i] = data[i] / two_NF
return dataSet , old_dataSet
#对权值矩阵进行归一化处理
def normalize_weight(com_weight):
for x in com_weight:
for data in x:
two_NF = cal2NF(data)
for i in range(len(data)):
data[i] = data[i] / two_NF
return com_weight
#得到获胜神经元的索引值
def getWinner(data , com_weight):
max_sim = 0
n,m,d = shape(com_weight)
mark_n = 0
mark_m = 0
for i in range(n):
for j in range(m):
if sum(data * com_weight[i,j]) > max_sim:
max_sim = sum(data * com_weight[i,j])
mark_n = i
mark_m = j
return mark_n , mark_m
#得到神经元的N邻域
def getNeibor(n , m , N_neibor , com_weight):
res = []
nn,mm , _ = shape(com_weight)
for i in range(nn):
for j in range(mm):
N = int(((i-n)**2+(j-m)**2)**0.5)
if N<=N_neibor:
res.append((i,j,N))
return res
#学习率函数
def eta(t,N):
return (0.3/(t+1))* (math.e ** -N)
#SOM算法的实现
'''
T:最大迭代次数
N_neibor:初始近邻数
'''
def do_som(dataSet , com_weight, T , N_neibor):
for t in range(T-1):
com_weight = normalize_weight(com_weight)
for data in dataSet:
n , m = getWinner(data , com_weight)
neibor = getNeibor(n , m , N_neibor , com_weight)
for x in neibor:
j_n=x[0];j_m=x[1];N=x[2]
#权值调整
com_weight[j_n][j_m] = com_weight[j_n][j_m] + eta(t,N)*(data - com_weight[j_n][j_m])
N_neibor = N_neibor+1-(t+1)/200
res = {}
N , M , _ =shape(com_weight)
for i in range(len(dataSet)):
n, m = getWinner(dataSet[i], com_weight)
key = n*M + m
if res.has_key(key):
res[key].append(i)
else:
res[key] = []
res[key].append(i)
return res
def draw(C , dataSet):
color = ['r', 'y', 'g', 'b', 'c', 'k', 'm' , 'd']
count = 0
for i in C.keys():
X = []
Y = []
datas = C[i]
for j in range(len(datas)):
X.append(dataSet[datas[j]][0])
Y.append(dataSet[datas[j]][1])
plt.scatter(X, Y, marker='o', color=color[count % len(color)], label=i)
count += 1
plt.legend(loc='upper right')
plt.show()
def loadDataSet(fileName): # 加载数据文件
fr = open(fileName)
dataMat=[]
for line in fr.readlines():
curLine = line.strip().split(",")
lineArr = []
lineArr.append(float(curLine[0]))
lineArr.append(float(curLine[1]))
dataMat.append(lineArr)
dataMat = mat(dataMat)
return dataMat
def file2matrix(path, delimiter):
recordlist = []
fp = open(path, "rb") # 读取文件内容
content = fp.read()
fp.close()
rowlist = content.splitlines() # 按行转换为一维表
# 逐行遍历 # 结果按分隔符分割为行向量
recordlist = [map(eval, row.split(delimiter)) for row in rowlist if row.strip()]
# 返回转换后的矩阵形式
return recordlist
# SOM算法主方法
def SOM(dataSet,com_n,com_m,T,N_neibor):
dataSet, old_dataSet = normalize(dataSet)
com_weight = initCompetition(com_n,com_m,shape(dataSet)[1])
C_res = do_som(dataSet, com_weight, T, N_neibor)
draw(C_res, dataSet)
draw(C_res, old_dataSet)
starttime = datetime.datetime.now()
dataSet = file2matrix("dataset2.txt",'\t')
SOM(dataSet,2,2,1000,2)
endtime = datetime.datetime.now()
print (endtime - starttime).seconds