参考

https://www.jianshu.com/p/7634eaea3e26

布隆过滤器

在日常生活中，包括在设计计算机软件时，我们经常要判断一个元素是否在一个集合中。比如在字处理软件中，需要检查一个英语单词是否拼写正确（也就是要判断它是否在已知的字典中）；在 FBI，一个嫌疑人的名字是否已经在嫌疑名单上；在网络爬虫里，一个网址是否被访问过等等。最直接的方法就是将集合中全部的元素存在计算机中，遇到一个新元素时，将它和集合中的元素直接比较即可。一般来讲，计算机中的集合是用哈希表（hash table）来存储的。它的好处是快速准确，缺点是费存储空间。当集合比较小时，这个问题不显著，但是当集合巨大时，哈希表存储效率低的问题就显现出来了。比如说，一个象 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人（spamer）的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的网络服务器。如果用哈希表，每存储一亿个 email 地址， 就需要 1.6GB 的内存（用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹 ，然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有 50%，因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB， 即十六亿字节的内存）。因此存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机，一般服务器是无法存储的。
今天，我们介绍一种称作布隆过滤器的数学工具，它只需要哈希表 1/8 到 1/4 的大小就能解决同样的问题。
布隆过滤器是由巴顿.布隆于一九七零年提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。我们通过上面的例子来说明起工作原理。
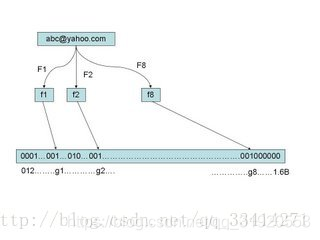
假定我们存储一亿个电子邮件地址，我们先建立一个十六亿二进制（比特），即两亿字节的向量，然后将这十六亿个二进制全部设置为零。对于每一个电子邮件地址 X，我们用八个不同的随机数产生器（F1,F2, …,F8） 产生八个信息指纹（f1, f2, …, f8）。再用一个随机数产生器 G 把这八个信息指纹映射到 1 到十六亿中的八个自然数 g1, g2, …,g8。现在我们把这八个位置的二进制全部设置为一。当我们对这一亿个 email 地址都进行这样的处理后。一个针对这些 email 地址的布隆过滤器就建成了。（见下图）

现在，让我们看看如何用布隆过滤器来检测一个可疑的电子邮件地址 Y 是否在黑名单中。我们用相同的八个随机数产生器（F1, F2, …, F8）对这个地址产生八个信息指纹 s1,s2,…,s8，然后将这八个指纹对应到布隆过滤器的八个二进制位，分别是 t1,t2,…,t8。如果 Y 在黑名单中，显然，t1,t2,…,t8 对应的八个二进制一定是一。这样在遇到任何在黑名单中的电子邮件地址，我们都能准确地发现。
布隆过滤器决不会漏掉任何一个在黑名单中的可疑地址。但是，它有一条不足之处。也就是它有极小的可能将一个不在黑名单中的电子邮件地址判定为在黑名单中，因为有可能某个好的邮件地址正巧对应个八个都被设置成一的二进制位。好在这种可能性很小。我们把它称为误识概率。在上面的例子中，误识概率在万分之一以下。
布隆过滤器的好处在于快速，省空间。但是有一定的误识别率。常见的补救办法是在建立一个小的白名单，存储那些可能别误判的邮件地址。

使用JAVA实现布隆过滤器

package edu.se;

import java.util.BitSet;

/**
 * @author ZhaoWeinan
 * @date 2018/10/28
 * @description
 */
public class BloomFileter {

    //使用加法hash算法，所以定义了一个8个元素的质数数组
    private static final int[] primes = new int[]{2, 3, 5, 7, 11, 13, 17, 19};
    //用八个不同的质数，相当于构建8个不同算法
    private Hash[] hashList = new Hash[primes.length];
    //创建一个长度为10亿的比特位
    private BitSet bits = new BitSet(256 << 22);

    public BloomFileter() {
        for (int i = 0; i < primes.length; i++) {
            //使用8个质数，创建八种算法
            hashList[i] = new Hash(primes[i]);
        }
    }

    //添加元素
    public void add(String value) {
        for (Hash f : hashList) {
            //算出8个信息指纹，对应到2的32次方个比特位上
            bits.set(f.hash(value), true);
        }
    }

    //判断是否在布隆过滤器中
    public boolean contains(String value) {
        if (value == null) {
            return false;
        }
        boolean ret = true;
        for (Hash f : hashList) {
            //查看8个比特位上的值
            ret = ret && bits.get(f.hash(value));
        }
        return ret;
    }

    //加法hash算法
    public static class Hash {

        private int prime;

        public Hash(int prime) {
            this.prime = prime;
        }

        public int hash(String key) {
            int hash, i;
            for (hash = key.length(), i = 0; i < key.length(); i++) {
                hash += key.charAt(i);
            }
            return (hash % prime);
        }
    }

    public static void main(String[] args) {

        BloomFileter bloomFileter = new BloomFileter();
        System.out.println(bloomFileter.contains("5324512515"));
        bloomFileter.add("5324512515");

        //维护1亿个在线用户
        for (int i = 1 ; i < 100000000 ; i ++){
            bloomFileter.add(String.valueOf(i));
        }

        long begin = System.currentTimeMillis();
        System.out.println(begin);
        System.out.println(bloomFileter.contains("5324512515"));
        long end = System.currentTimeMillis();
        System.out.println(end);
        System.out.println("判断5324512515是否在线使用了:" + (begin - end));
    }
}

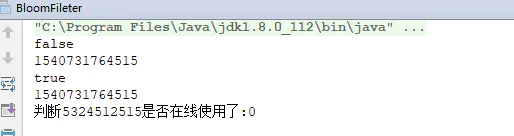
这段代码是构建了一个10亿位的bitSet，然后把一亿个userId加入到了我们的布隆过滤器中，最近判断5324512515这个userId是否登录，打出代码的执行时间

维护了1亿个userId以后检索5324512515是否登录，代码执行时间很短

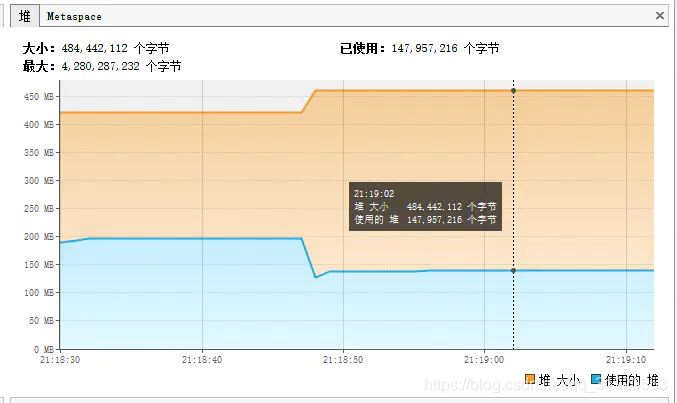
在让我们来看看内存占用的情况

jvm整个的内存情况

再来看看BloomFileter这个类的实例，就占用了100多MB
实例的大小

看来布隆过滤器对于储存的效率确实很高

布隆过滤器的误识别问题
布隆过滤器的好处在于快速、省空间，但是有一定的误识别率，这个概率很小，要计算出现误识别的概率并不难，下面贴一段书上的话
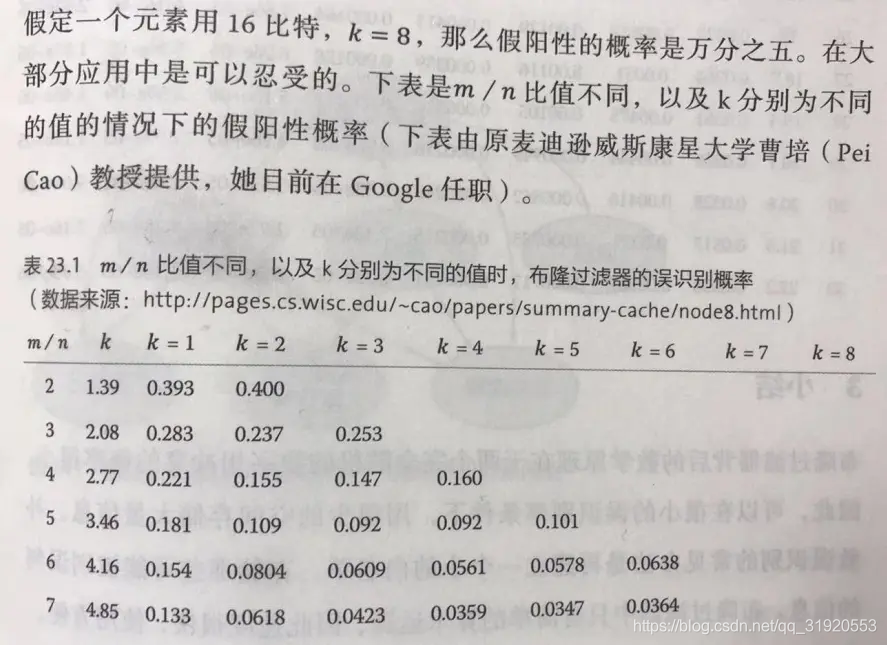
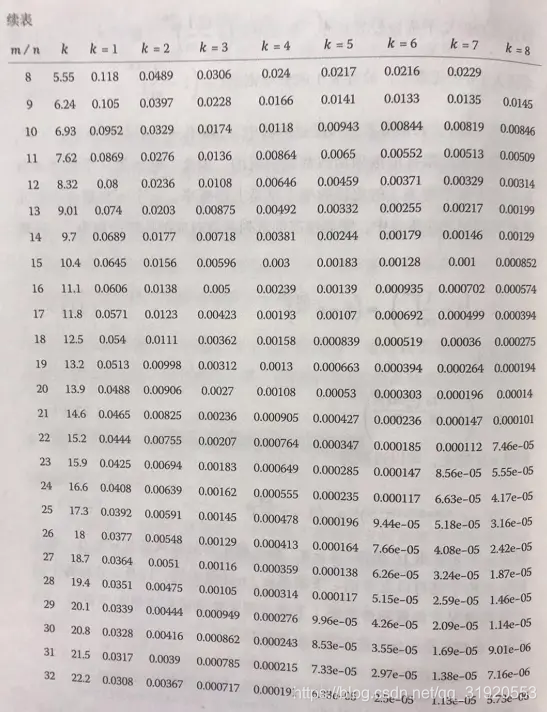
假定布隆过滤器有m比特，里面有n个元素，每个元素对应k个信息指纹的hash函数，在这个布隆过滤器插入一个元素，那么比特位被设置成1的概率为1/m，它依然为0的概率为1-1/m，那么k个哈希函数都没有把他设置成1的概率为1-1/m的k次方，一个比特在插入了n个元素后，被设置为1的概率为1减1-1/m的kn次方，最后书上给出了一个公式，在这里就不贴了，就贴一个表吧，是m/n比值不同，以及K分别为不同的值得情况下的假阳性概率：

书上的表，直接拍下来的

书上的表，直接拍下来的