最近有点事儿，没有继续写，连emsp缩进都想了半天，实属不该。最近CVPR2020一篇文章引起了注意。特来拜读，如有错误，希望指正。

基于shift图卷积网络的骨架动作识别

Abstract

  利用骨骼数据进行动作识别是计算机视觉领域的研究热点。近年来，将人体骨骼建模为时空图的图卷积网络（GCNs）取得了显著的性能。然而，基于gcn方法的计算复杂度相当高，通常一个动作样本的计算复杂度超过15 GFLOPs。最近的作品甚至达到100 GFLOPs。另一个缺点是空间图和时间图的感受野都不灵活。虽然一些工作通过引入增量式自适应模块来增强空间图的表达能力，但其性能仍然受到规则GCN结构的限制。本文提出了一种改进的移位图进化网络（Shift-GCN）来克服这两个缺点。Shift-GCN不使用heavy regular 图卷积，而是由新的移位图操作和轻量点卷积组成，其中移位图操作为空间图和时间图提供了灵活的感受野。在基于骨架动作识别的三个数据集上，本文提出的Shift-GCN算法的计算复杂度明显比目前SOTA方法少10倍以上。

1.Introduction

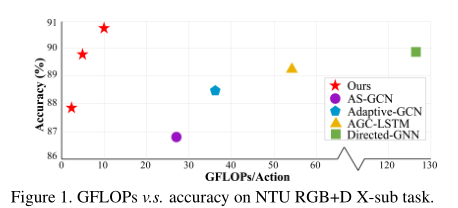
  传统的依靠STGCN的人体动作识别通常引入增量模块以增强表达能力和网络capacity。但是有两个缺点：(1)计算复杂度太高。ST-GCN达到16.2 GFLOPS，由于引入了增量模块和多流融合策略，有向无环图网络甚至达到了100 GFLOPS。(2)空间图和时间图的接受域都是启发式预定义的，虽然双流网络进行了空间邻接矩阵的学习，但是表达能力仍然受到GCN空间规则的限制。
  本文提出了移位图卷积网络（shift-GCN）来解决这两个缺点。Shift-GCN的灵感来自Shift CNNs，它使用轻量级的移位操作作为2D卷积的替代，并且可以通过简单地改变移位距离来调整感受野。提出的Shift GCN由空间Shift 图卷积和时间Shift 图卷积两部分组成。对于空间骨架图，作者提出了一种空间移位图操作，将信息从相邻节点转移到当前卷积节点，而不是使用三个具有不同邻接矩阵的gcn来获得足够的感受野。
  通过将空间移位图操作与点卷积交错，信息在空间维度和通道维度上混合。具体来说，我们提出了两种空间移位图操作：局部移位图操作和非局部移位图操作。对于局部移位图操作，接收场由身体物理结构指定。在这种情况下，不同的节点具有不同数量的邻居，因此分别为每个节点设计了局部移位图操作。然而，局部移位图操作有两个缺点：

• 接受域是heuristically(试探性的/启发式)的预定义和局部的，不适合于建模骨骼之间的多样关系。
• 由于不同节点的移位操作不同，一些信息直接被丢弃。为了解决这两个缺点，我们提出了一种非局部移位图操作，使得每个节点的接收场覆盖整个骨架图，并自适应地学习关节之间的关系。大量的烧蚀实验表明，即使规则空间图卷积的邻接矩阵是可学习的，我们的非局部移位图卷积仍优于规则空间图卷积。

  对于时间骨架图，该图构造时间维度连续的帧的连接来实现。提出了两种时态移位图操作：单纯的时态移位图操作和自适应的时态移位图操作。单纯的时态移位图操作的感受野是人工设置的，这对于时间建模是不理想的：(1)不同的层可能需要不同的时间感受野。(2) 不同的数据集可能需要不同的时间感受野。这两个问题也存在于规则的一维时间卷积中，其核大小是手动设置的。我们的自适应时间移位图操作通过自适应地调整接收场来解决这两个问题。大量的消融研究表明，自适应时移图卷积比常规时移图卷积有更高的效率。
  本文的主要工作如下：

• 1）提出了两种空间骨架图建模的空间移位图操作。非局部空间移位图运算在计算上是有效的，并且取得了很强的性能。
• 2） 针对时间骨架图模型提出了两种时间移位图操作。自适应时间移位图操作可以自适应地调整接收场，并且在计算复杂度上优于常规时间模型。
• 3)在基于骨架的动作识别的三个数据集上，本文提出的移位GCN算法的计算量比现有的方法少10倍以上。
  

2. Preliminaries

2.1 基于GCN的骨骼动作识别

  基于时空图卷积已经成功的应用于基于骨骼动作识别。空间图卷积一般将邻接矩阵分为3个部分：(1)本征点(2)离心点(3)向心点。时间卷积是通过连接连续帧的节点在时间维度上进行1D卷积作为时间卷积，通常设定卷积核为9。然而缺点是:(1)计算量太大。(2)感受野受限，表达能力受到规则GCN结构的限制。

2.2. Shift CNNs

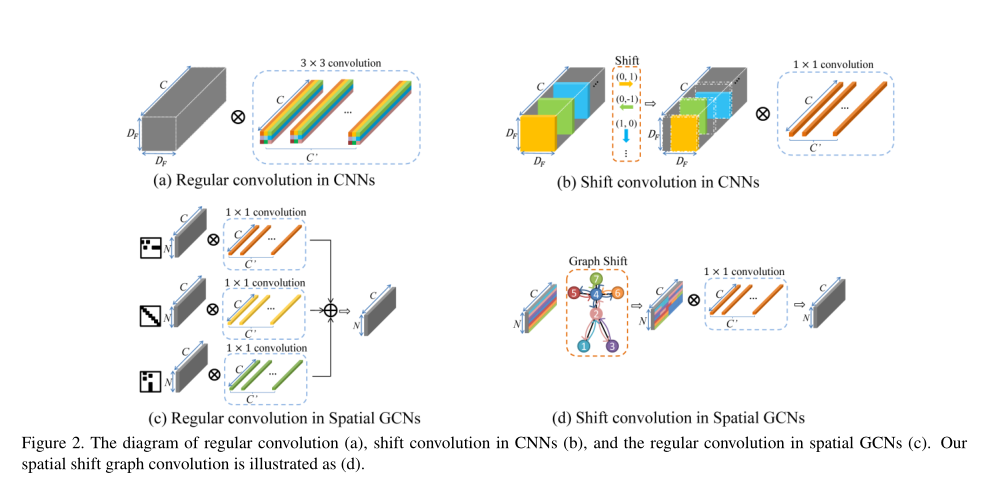
  设$\mathrm{F}\in {\mathbb{R}}^{{\mathrm{D}}_{\mathrm{F}}\times {\mathrm{D}}_{\mathrm{F}}\times \mathrm{C}}$为输入特征，其中$D_F$为特征图大小，$C$为信道大小。如图2(a)所示,正则卷积核是张量$\mathrm{K}\in {\mathbb{R}}^{{\mathrm{D}}_{\mathrm{K}}\times {\mathrm{D}}_{\mathrm{K}}\times \mathrm{C}\times {\mathrm{C}}^{\prime }}$，其中$D_K$是核的大小。规则卷积的FLOPS为$D_K^2\times D_F^2\times C\times C^{\prime }$。
  Shift convolution 是CNNs中常规卷积的有效替代方法。如图2(b)所示，移位卷积由两个操作组成:(1)在不同方向上shift不同的通道(2)应用点卷积来跨通道交换信息。移位卷积的FLOPs是$D_F^2\times C\times C^{\prime }$
  移位卷积的另一个优点是感受野的灵活性。移位卷积可以通过简单地增加移位距离来扩大其感受野，而不必使用较大的卷积核和增加计算量。将每个通道的移位值表示为一系列向量$S_i,i=1,2,\cdot \cdot \cdot ,C$其中$S_i=(x_i,y_i)$表示2D移位向量。移位卷积的感受野可以表示为相反方向上的每个移位向量的并集： R = { − S 1 } ∪ { − S 2 } ∪ . . . { − S C } (2) R = \{-S_1\} \cup \{-S_2\} \cup ... \{-S_C\} \tag{2} R={−S1​}∪{−S2​}∪...{−SC​}(2)例如，如果 x i ∈ { − 1 , 0 , 1 } ， y i ∈ { − 1 , 0 , 1 } x_i \in \{-1,0,1\}，y_i \in \{-1,0,1\} xi​∈{−1,0,1}，yi​∈{−1,0,1}，则感受野扩大到$3\times 3$。

3. Shift graph convolutional network

3.1. Spatial shift graph convolution

  引入从CNNs到GCNs的移位操作是具有挑战性的，因为图的特征不像图像的特征映射那样是有序的。在本小节中，首先讨论从CNNs到空间GCNs的类比。在此基础上，提出了空间骨架图的空间移位图卷积方法。

CNNs与GCNs的类比

  CNNs中的规则卷积核可以看作是几个点卷积核的融合，每个核在指定的位置上操作，如图2(a)所示，颜色不同。例如，3×3卷积核是9个点卷积核的融合，每个点卷积核在“左上”、“上”、“右上”…“右下角”。
  类似地，空间GCNs中的规则卷积核是3个点卷积核的融合，每个核在指定的空间分区上操作，如图2©所示，颜色不同。如第2.1节所述，空间分区由3个不同的相邻矩阵指定，分别表示“向心”、“root”、“离心”。
  CNNs中的移位卷积包含移位操作和点卷积核，其中感受野是由shift操作，如图2(b)所示。
  因此，移位图卷积应包含移位图操作和点方向卷积，如图2(d)所示。移位图操作的主要思想是将相邻节点的特征转移到当前卷积节点。具体地，我们提出了两种移位图卷积：局部移位图卷积和非局部移位图卷积。

Local shift graph convolution

  对于局部移位图卷积，感受野由人体的物理结构来指定，而人体的物理结构是由骨骼数据集预先定义的。在该设置中，移位图操作在身体物理图的相邻节点之间进行。
  由于人体关节之间的连接不像CNN特征那样有序，不同的节点有不同数量的邻居。设$v$表示一个节点, B v = { B v 1 , B v 2 , ⋅ ⋅ ⋅ , B v n } B_v=\{B^1_v,B^2_v,···,B^n_v\} Bv​={Bv1​,Bv2​,⋅⋅⋅,Bvn​}表示它的邻居节点集，其中$n$表示$v$的邻居节点数，我们将节点$v$的通道平均划分为$n+1$个分区。我们让第一部分保留$v$的特征，其他$n$个部分分别从$B_v^1,B_v^2,\cdot \cdot \cdot ,b_v^n$移位。设$\mathrm{F}\in {\mathbb{R}}^{\mathrm{N}\times \mathrm{C}}$代表单帧特征,$\tilde{\mathrm{F}}\in {\mathbb{R}}^{N\times C}$代表相应的移位特征。我们对$\mathrm{F}$的每个节点进行移位操作。$${\tilde{\mathrm{F}}}_v={\mathrm{F}}_{(\mathrm{v},:\mathrm{c})}||{\mathrm{F}}_{({\mathrm{B}}_{\mathrm{v}}^1,\mathrm{c}:2\mathrm{c})}||{\mathrm{F}}_{({\mathrm{B}}_{\mathrm{v}}^2,2\mathrm{c}:3\mathrm{c})}||...||{\mathrm{F}}_{({\mathrm{B}}_{\mathrm{v}}^{\mathrm{n}},\mathrm{n}\mathrm{c}:)}\text{\hspace{1em}(3)}$$其中$c=\lfloor \frac{C}{n+1}\rfloor$,$\mathrm{F}$的索引采用Python表示法,||表示按通道连接。
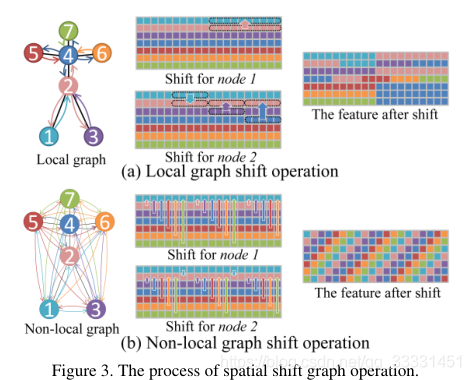
  为了说明局部移位图操作的直观性，我们以7个节点和20个通道的微小图特征为例，如图3(a)所示。我们使用节点1和节点2作为两个例子。对于节点1，它只有一个邻居节点，因此它的通道被分成两个分区。第一个分区保留节点1的特征，而第二个分区从节点2特征移动。另一个例子是，节点2有三个邻居节点，所以它的通道被分成四个分区。第一个分区保留了节点2的特性，而其他三个分区则从节点1、节点3、节点4移动。
  移位操作后的特征如图3（a）所示。在移位特征中，每个节点从其感受野获取信息。将局部移位图运算与逐点卷积相结合，得到局部移位图卷积。

Non-local shift graph convolution

  局部移位图卷积有两个缺点:(1)一些信息没有得到充分利用。对于图3(a)中的示例,在移位操作期间,节点3中的最后四分之一通道被直接丢弃。这是因为不同的节点有不同数量的邻居。(2)最近的研究表明，对于骨骼动作识别，仅考虑局部连接是不理想的。例如，两只手之间的关系对于识别“拍手”和“阅读”等动作很重要，但在身体结构上，两只手却相距甚远。
  我们提出了一个简单的解决方案来解决这两个缺点：使每个节点的接收场覆盖整个骨架图。我们称之为非局部移位图运算。
  非局部移位图操作如图3(b)所示。在给定空间骨架特征映射$\mathrm{F}\in {\mathbb{R}}^{\mathrm{N}\times \mathrm{C}}$的情况下，第i个通道的移位距离为$i\mathrm{m}\mathrm{o}\mathrm{d}N$，移位后的通道用于填充相应的空空间。节点1和节点2的移位操作如示例所示。在非局部移位之后，该特征看起来像一个螺旋，使得每个节点从所有其他节点获取信息，如图3(b)所示。将非局部移位图运算与逐点卷积相结合，得到非局部移位图卷积。
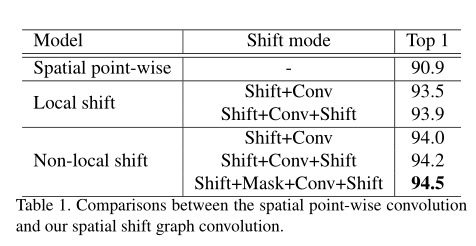
  在非局部移位图卷积中，不同节点之间的连接强度是相同的。但是人类骨骼的重要性是不同的。因此，我们引入了一种自适应的非局部移位机制。我们计算移位特征和可学习掩码之间的元素积：$${\tilde{\mathrm{F}}}_M=\tilde{\mathrm{F}}\circ Mask=\tilde{\mathrm{F}}\circ (tanh(\mathrm{M})+1)\text{\hspace{1em}(4)}$$  规则空间图卷积的FLOPs为$3\times (NC{C}^{\prime }+N^2{C}^{\prime })$。移位空间图卷积的触发器约为$NC{C}^{\prime }$，其规则空间图卷积权重是变换空间图卷积的3倍以上。与仅使用三个邻接矩阵来建立骨架关系的规则图卷积相比，我们的非局部移位操作可以模拟不同通道中不同骨架之间的各种关系。第4.2.1节中的实验表明，即使规则GCN中的相邻矩阵被设置为可学习的，我们的非局部移位GCN也比规则GCN具有更好的性能。

3.2. Temporal shift graph convolution

  在为每个骨架帧建立轻量级空间移位图卷积模型之后，设计轻量级时间移位图卷积来对骨架序列进行建模。

Naive(简单的，纯的) temporal shift graph convolution

  图的时间处理是在时间维度上连接连续帧来构造。因此，CNNs中的移位操作可以直接扩展到时域。将通道平均划分为$2u+1$个分区，每个分区分别具有$-u,-u+1,\cdot \cdot \cdot \cdot ,0,\cdot \cdot \cdot \cdot ,u-1,u$的时间移位距离。移位后的通道被截断，空通道用零填充。在移位操作之后，每个帧从其相邻帧获取信息。通过将这种时间移位操作与时间点卷积相结合，我们得到了简单时间移位图卷积。
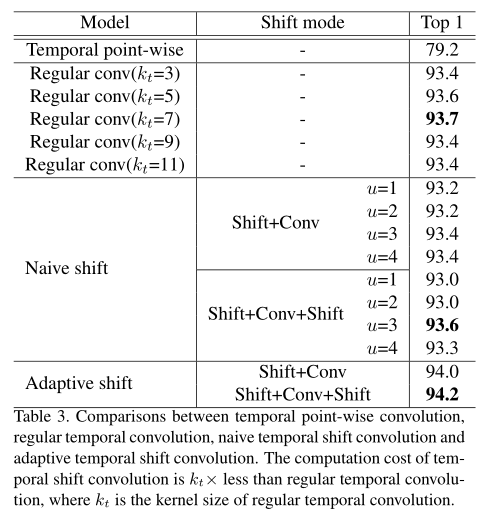
  一般情况下，基于GCN的动作识别中规则时间卷积的核大小为9。与常规时间卷积相比，纯时间移位图卷积的计算量减少了9倍。

Adaptive temporal shift graph convolution

  虽然简单时移图卷积是轻量级的，但其超参数$u$的设置是手动的。这导致了两个缺点:(1)最近的研究表明，在视频分类任务中，不同的层需要不同的时间感受野。对$u$的所有可能组合的彻底搜索是困难的。(2) 不同的数据集可能需要不同的时间感受野，这限制了简单时间移位图卷积的泛化能力。这两个缺点也存在于规则时间卷积中，其核大小是手动设置的。
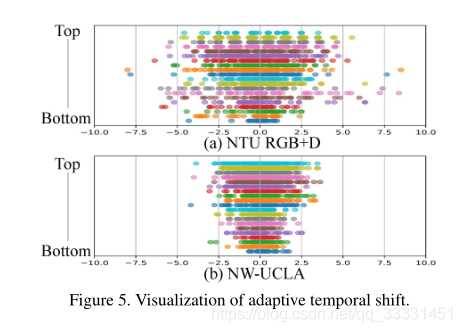
  为了解决这两个缺点，我们提出了一种自适应的时间移位图卷积。给定骨架序列特征$\tilde{\mathrm{F}}\in {\mathbb{R}}^{N\times T\times C}$，每个通道都有一个可学习的时移参数$S_i$,$i=1,2，\cdot \cdot \cdot ，C$,我们将时移参数从整数约束放宽到实数。用线性插值法计算非整数位移:$${\tilde{\mathrm{F}}}_{(v,t,i)}=(1-\lambda )\cdot {\mathrm{F}}_{(\mathrm{v},\lfloor \mathrm{t}+{\mathrm{S}}_{\mathrm{i}}\rfloor ,\mathrm{i})}+\lambda {\mathrm{F}}_{(\mathrm{v},\lfloor \mathrm{t}+{\mathrm{S}}_{\mathrm{i}}\rfloor +1,\mathrm{i})}\text{\hspace{1em}(5)}$$  式中，$\lambda =S_i-\lfloor S_i\rfloor$。此操作是可微的，可以通过反向传播进行训练。通过将此操作与点卷积相结合，我们得到了自适应的时间移位卷积。自适应时间移位操作是轻量级的，具有C个额外参数和$2NCT$额外FLOPs。与点卷积相比，这种计算代价是可以忽略的。第4.2.2节证明了自适应时移图卷积的有效性和效率。

3.3. Spatiotemporal shift GCN

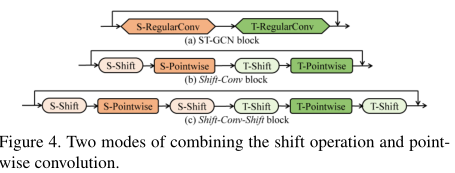
  为了与目前SOTA的方法进行比较，我们使用相同的主干（ST-GCN）来构建我们的时空位移GCN。ST-GCN骨干网由一个输入块和9个残差块组成，每个块包含一个规则的空间卷积和一个规则的时间卷积。我们用空间移位操作和空间点卷积来代替规则空间卷积。用时间移位操作和时间逐点卷积来代替常规的时间卷积。
  将移位操作与逐点卷积相结合有两种模式：移位Conv和移位Conv shift，如图4所示。Shift-Conv-Shift模式具有更大的接收场，通常可以获得更好的性能。我们在烧蚀研究中证实了这一现象。

4. Experiments

4.2. Ablation Study

4.2.1 Spatial shift graph convolution

4.2.2 Temporal shift graph convolution

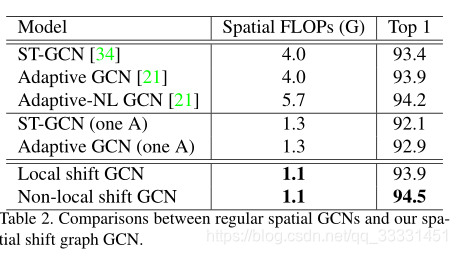
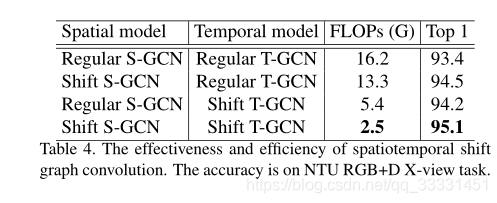
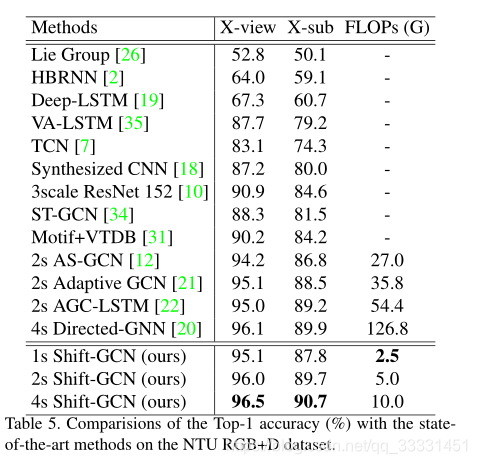
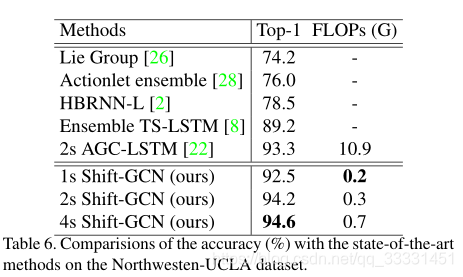
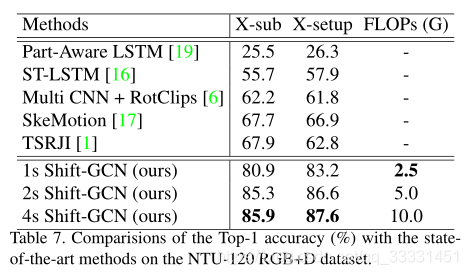
4.3. Comparison with the state-of-the-art