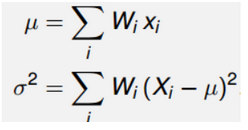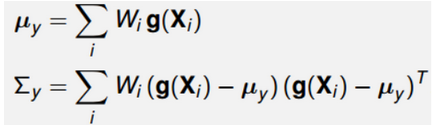文章目录
一、 非线性处理/测量模型
我们知道KF是面临的主要问题就是非线性处理模型(比如说CTRV)和非线性测量模型(RADAR测量)的处理。我们从概率分布的角度来描述这个问题:
对于我们想要估计的状态,在 k k k时刻满足均值为 x k x_k xk,方差为 P k P_k Pk 这样的一个高斯分布,这个是我们在k时刻的 后验(Posterior)(如果我们把整个卡尔曼滤波的过程迭代的来考虑的话),现在我们以这个后验为出发点,结合一定的先验知识(比如说CTRV运动模型)去估计我们在 k+1时刻的状态的均值和方差,这个过程就是卡尔曼滤波的预测,如果变换是线性的,那么预测的结果仍然是高斯分布,但是现实是我们的处理和测量模型都是非线性的,结果就是一个不规则分布,KF能够使用的前提就是所处理的状态是满足高斯分布的,为了解决这个问题,EKF是寻找一个线性函数来近似这个非线性函数,而UKF就是去找一个与真实分布近似的高斯分布。
UKF的基本思路就是: 近似非线性函数的概率分布要比近似非线性函数本身要容易!
那么如何去找一个与真实分布近似的高斯分布呢?——找一个与真实分布有着相同的均值和协方差的高斯分布。那么如何去找这样的均值和方差呢?——无损变换。
UT变换是用固定数量的参数去近似一个高斯分布,其实现原理为:在原先分布中按某一规则取一些点,使这些点的均值和协方差与原状态分布的均值和协方差相等;将这些点代入非线性函数中,相应得到非线性函数值点集,通过这些点集可求取变换的均值和协方差。对任何一种非线性系统,当高斯型状态微量经由非线性系统进行传递,进而利用这组采样点能获取精确到三阶矩的后验均值和协方差。
UT变换的特点是对非线性函数的概率密度分布进行近似,而不是对非线性函数进行近似,即使系统模型复杂,也不增加算法实现的难度;而且所得到的非线性函数的统计量的准确性可以达到三阶;除此之外,它不需要计算雅可比矩阵,可以处理不可导非线性函数。
二、无损(迹)变换(Unscented Transformation)
通过一定的手段产生的这些sigma点能够代表当前的分布,然后将这些点通过非线性函数(系统模型)变换成一些新的点,然后基于这些新的sigma点计算出一个高斯分布(带有权重地计算出来)
2.1 一个高斯分布产生sigma point
UT变换基本原理如下:假设一个非线性系统 y = g ( x ) y=g(x) y=g(x),其中 x x x为 n n n维状态向量,并已知其平均值为 x ‾ \overline x x,方差为 P x P_x Px,则可以经过UT变换构造 2 n + 1 2n+1 2n+1个Sigma点,同时构造相应的权值,进而得到y的统计特性。
构造sigma点集的计算公式为:
其中的 λ 是比例因子,根据公式,λ 越大, sigma点就越远离状态的均值,λ 越小, sigma点就越靠近状态的均值。
λ
=
α
(
n
2
+
k
)
−
n
\lambda = \alpha(n^2+k)-n
λ=α(n2+k)−n
( ( n + λ ) P x ) i (\sqrt {(n+\lambda)P_x})_i ((n+λ)Px)i表示矩阵方根 ( n + λ ) P x \sqrt {(n+\lambda)P_x} (n+λ)Px的第 i i i列。
可以使用Cholesky分解计算出矩阵 L ( Σ = L L T ) L(Σ = LL^T) L(Σ=LLT)
//calculate square root of P
MatrixXd A=P.llt().matrix();
/**
* @brief compute sigma points 生成sigma points
* @param mean mean
* @param cov covariance
* @param sigma_points calculated sigma points
*/
void computeSigmaPoints(const VectorXt& mean, const MatrixXt& cov, MatrixXt& sigma_points) {
const int n = mean.size(); // 状态x的维度
assert(cov.rows() == n && cov.cols() == n);
Eigen::LLT<MatrixXt> llt;
llt.compute((n + lambda) * cov);
MatrixXt l = llt.matrixL();
sigma_points.row(0) = mean;
for (int i = 0; i < n; i++) {
sigma_points.row(1 + i * 2) = mean + l.col(i);
sigma_points.row(1 + i * 2 + 1) = mean - l.col(i);
}
}
x ‾ \overline x x周围Sigma点的分布状态由 α \alpha α决定,调节 α \alpha α可以降低高阶项的影响,通常设为一个较小的正数,这里选取 α = 0.001 \alpha=0.001 α=0.001。 k k k的取值没有具体设定限制,但至少应当保证矩阵 ( n + λ ) P x {(n+\lambda)P_x} (n+λ)Px为半正定矩阵,通常设置 k = 0 k=0 k=0。
2.2 sigma point的权重
权重的选择应该满足下面的性质,假设y=g(x)
因此权重w的公式如下:
如果x是高斯分布,
β
=
2
\beta=2
β=2是最佳的
// 均值的权重
weights[0] = lambda / (N + lambda);
for (int i = 1; i < 2 * N + 1; i++) {
weights[i] = 1 / (2 * (N + lambda));
}
2.3 预测新的状态分布(predict过程)
- 使用系统方程更新所有sigma points的状态
σ ^ = f ( σ ) \hat \sigma=f(\sigma) σ^=f(σ)
// 遍历每天一个sigma points 更新他们的状态
for (int i = 0; i < S; i++)
{
sigma_points.row(i) = system.f(sigma_points.row(i), control);
}
- 加权新的sigma points 预测估计值和协方差
z ^ = ∑ w i σ i \hat z=\sum w_i\sigma_i z^=∑wiσi
P ^ = ∑ w i ( σ i − z ^ ) ( σ i − z ^ ) T + Q ( 过 程 噪 声 ) \hat P=\sum w_i(\sigma_i-\hat z)(\sigma_i-\hat z)^T+Q_{(过程噪声)} P^=∑wi(σi−z^)(σi−z^)T+Q(过程噪声)
const auto& Q = process_noise;
// unscented transform
VectorXt mean_pred(mean.size());
MatrixXt cov_pred(cov.rows(), cov.cols());
mean_pred.setZero();
cov_pred.setZero();
for (int i = 0; i < S; i++) {
mean_pred += weights[i] * sigma_points.row(i);
}
for (int i = 0; i < S; i++) {
VectorXt diff = sigma_points.row(i).transpose() - mean_pred;
cov_pred += weights[i] * diff * diff.transpose();
}
cov_pred += Q;
mean = mean_pred;
cov = cov_pred;
2.4 更新滤波器(measurement过程)
参考:https://blog.csdn.net/qq_34461089/article/details/88989076#commentBox