前言
活动地址:CSDN21天学习挑战赛
本文内容源于对《数据结构(C语言版)》(第2版)、王道讲解学习所得心得、笔记整理和总结。
本文主要针对 2-路归并排序,因为 2-路归并最为简单和常用。2-路归并排序算法与线性表的应用之 “ 顺序有序表的合并 ” 算法类似(见下方链接)。
在本文最后的练习中,以举例子说明该排序方法,配以图文,讲解详细(含408真题)。
可搭配以下链接进行学习:
【考研】线性表的应用之有序表的合并_住在阳光的心里的博客-CSDN博客
【考研】数据结构考点——链式基数排序_住在阳光的心里的博客-CSDN博客
【考研】数据结构考点——快速排序(重点,含408真题)_住在阳光的心里的博客-CSDN博客
【考研】《数据结构》知识点总结.pdf_考研数据结构知识点总结背诵-其它文档类资源-CSDN下载
目录
一、归并排序(Merging Sort)
1、定义
将两个或两个以上的有序表合并成一个有序表的过程。将两个有序表合并成一个有序表的过程称为2-路归并。
2、算法思想
(1)假设初始序列含有 n 个记录,则可看成是 n 个有序的子序列,每个子序列的长度为1;
(2)然后两两归并,得到 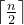
(3)再两两归并,..... 如此重复,直至得到一个长度为 n 的有序序列为止。
3、核心操作
将待排序序列中前后相邻的两个有序序列归并为一个有序序列。
二、相邻两个有序子序列的归并
(一)算法步骤
设两个有序表存放在同一数组中相邻的位置上:R[low..mid] 和 R[mid+1..high],每次分别从两个表中取出一个记录进行关键字的比较,将较小者放人 T[low..high] 中,重复此过程,直至其中一个表为空,最后将另一非空表中余下的部分直接复制到 T 中。
(二)算法代码
// 将有序表 R[low..mid] 和 R[mid+1..high] 归并为有序表 T[low..high]
void Merge (RedType R[],RedType &T[], int low, int mid, int high){
i = low;
j = mid + 1;
k = low;
while(i <= mid && j<= high){ //将 R 中记录由小到大地并入 T 中
if(R[i].key <= R[j].key) T[k++] = R[i++];
else T[k++] = R[j++];
}
//只有一个 while 循环会被执行
while(i <= mid) T[k++] = R[i++]; //将剩余的 R[low..mid] 复制到 T 中
while(j <= high) T[k++] = R[j++]; //将剩余的 R[j..high] 复制到 T 中
}
(三)分析
假设每个子序列的长度为 h ,则一趟归并排序需调用 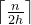
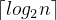
与快速排序类似,2-路归并排序也可以利用划分为子序列的方法递归实现。首先把整个待排序序列划分为两个长度大致相等的子序列,对这两个子序列分别递归地进行排序,然后再把它们归并。
三、归并排序
(一)算法步骤
2-路归并排序将 R[low..high] 中的记录归并排序后放入 T[low. high] 中。当序列长度等于1时,递归结束,否则:
1、将当前序列一分为二,求出分裂点
2、对子序列 R[low..mid] 递归,进行归并排序,结果放入 S[low..mid] 中;
3、对子序列 R[mid + 1..high] 递归,进行归并排序,结果放入 S[mid + 1..high] 中;
4、调用算法 Merge,将有序的两个子序列 S[low..mid] 和 S[mid+ 1..high] 归并为一个有序的序
列 T[low..high] 。
(二)算法代码
// R[low..high] 归并排序后放入 T[low..high] 中
void MSort (RedType R[], RedType &T[], int low, int high){
if (1ow == high) T[low] = R[low];
else{
mid = (low + high) / 2; //将当前序列一分为二,求出分裂点 mid
//对子序列 R[low..mid] 递归归并排序,结果放入 S[low..mid]
MSort (R, S, low, mid);
//对子序列 R[mid+1..high] 递归归并排序,结果放入 S[mid+1..high]
MSort (R, S, mid+1,high) ;
//将 S[low..mid] 和 S[mid+1..high] 归并到 T[low..high]
Merge (S, T, low, mid, high) ;
}
}
//对顺序表L做归并排序
void MergeSort (SqList &L){
MSort(L.r, L.r, 1, L.length);
}
(三)算法分析
1、时间复杂度
当有 n 个记录时,需进行 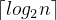
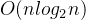
2、空间复杂度
用顺序表实现归并排序时,需要和待排序记录个数相等的辅助存储空间,所以空间复杂度为O(n)。
(四)算法特点
1、是稳定排序。
2、可用于链式结构,且不需要附加存储空间,但递归实现时仍需要开辟相应的递归工作栈。
3、注意:一般而言,对于 n 个元素进行 k 路归并排序时,排序的趟数 m 满足 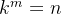
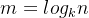
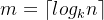
四、 练习
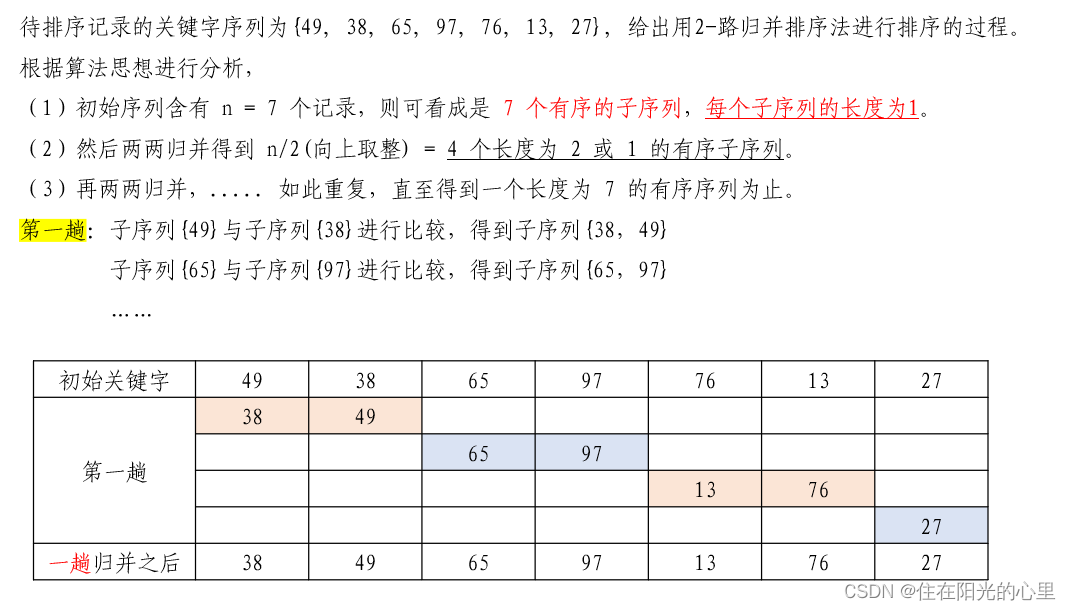
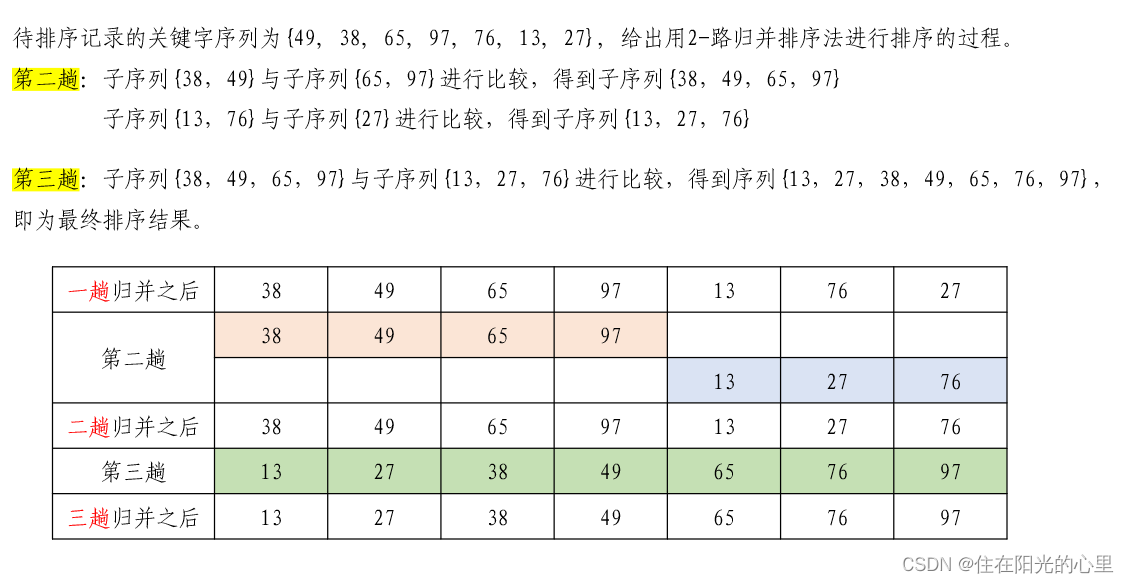
1、已知待排序记录的关键字序列为{49, 38, 65, 97, 76, 13, 27}, 给出用2-路归并排序法进行排序的过程。
解:如下图所示。
2、下述几种排序方法中,要求内存最大的是( C )
A. 希尔排序 B. 快速排序 C. 归并排序 D. 堆排序
解:用顺序表实现归并排序,需要内存O(n)。
而希尔排序、快速排序、堆排序的空间复杂度分别为O(1)、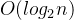
所以要求内存最大的是归并排序。
3、以下排序算法中,( C )在一趟结束后不一定能选出一个元素放在其最终位置上。
A. 简单选择排序 B. 冒泡排序 C. 归并排序 D. 堆排序
解:插入排序和归并排序都不能保证在一趟结束后一定能选出一个元素放在其最终位置上。
4、在下列排序方法中,排序过程中比较次数的数量级与序列初始状态无关的是( A )
A. 归并排序 B. 插入排序 C. 快速排序 D. 冒泡排序
解:选择排序和归并排序的比较次数与序列初始状态无关。
5、若对27个元素只进行三趟多路归并排序,则选取的归并路数最少为( B )
A. 1 B. 3 C. 2 D. 4
解: 一般而言,对于 n 个元素进行 k 路归并排序时,排序的趟数 m 满足 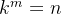
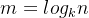
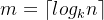
所以选取的归并路数最少为 ![k =\sqrt[3]{27}=3](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9rJTIwJTNEJTVDc3FydCU1QjMlNUQlN0IyNyU3RCUzRDM%3D)
6、在内部排序时,若选择了归并排序而未选择插入排序,则可能的理由是( B )。
Ⅰ.归并排序的程序代码更短 Ⅱ.归并排序的占用空间更少
Ⅲ.归并排序的运行效率更高
A. 仅Ⅰ、Ⅱ B. 仅Ⅲ C. 仅 Ⅱ D. 仅Ⅰ、Ⅲ
解:归并排序代码比选择插入排序更复杂,两者的时间复杂度分别是 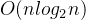
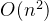
7、将两个各有 N 个元素的有序表合并成一个有序表,最少的比较次数是( A ),最多的比较次数是( B )。
A. N B. 2N - 1 C. 2N D. N - 1
解:比较次数最少的情况:一个表中的最小元素比另一个表中的最大元素还大。(仅比较 N 次)
比较次数最多的情况:两个表中的元素依次间隔地比较时,即 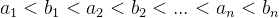
8、一组经过第一趟 2- 路归并排序后的记录的关键字为{25,50,15,35,80,85,20,40,36,70},其中包含 5 个长度为 2 的有序表,用 2- 路归并排序方法对该序列进行第二趟归并后的结果为()。
A.15,25,35,50,80,20,85,40,70,36
B.15,25,35,50,20,40,80,85,36,70
C.15,25,50,35,80,85,20,36,40,70
D.15,25,35,50,80,20,36,40,70,85
解:{25,50,15,35,80,85,20,40,36,70},元素个数一共 10 个。初始序列可看成10个有序的子序列,每个子序列的长度为1。
一趟二路归并排序后,为 5 个长度为 2 的有序表,即为 {25,50},{15,35},{80,85},{20,40} 和 {36,70}。
第二趟归并排序,所以每 4 个元素放在一起归并,即可将序列划分为 {25,50,15,35} ,{80,85,20,40} 和 {36,70},分别对它们进行排序后有{15,25,35,50},{20,40,80,85} 和 {36,70},所以选 B。