经过逻辑电路的设计,我们得到了全加器,经过不同全加器的设置我们可以开展定点数的加减运算,然后根据加减运算可以设计乘除运算乃至浮点数运算。因此,定点数加减运算的ALU设计学习非常重要。
目录
定点数加法运算
定点数补码加法满足以下公式:
下面展示了一个定点数加法的例子:
设X = +10010, Y=-10101, 求X+Y
解:使用补码运算
[X] = 010010 ,[Y] = 101011
得到
[X]+[Y] = 111101,求补得到:
X+Y = -00011定点数加法器设计
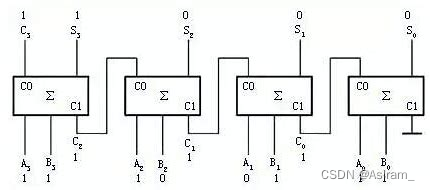
根据定点数补码加法可以基于全加器设计加法器:
上面是4位加法器的示意图。可以看到它是由4个全加器串接在一起的。其中Si指示了得数的各位数值,C3则指示是否溢出。
定点数减法运算
定点数补码减法满足以下公式:
那么,根据这种方法,我们就可以根据和加法器相同的框架计算减法。但是有一个问题:怎么得出![[-Y]_c](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUItWSU1RF9j)
求解-Y的补码规则如下:
从右向左:遇到第一个1以前直接输出,遇到1以后按位取反输出。注意:第一个1是不取反的。
设Y = -10100,求-Y的补码。
解:[Y] = 101100
[-Y] = 010100
上述计算表明,-Y = +10100
事实确实如此。
下面是一个定点数减法的例子:
设X=+10101,Y = -00010,求X-Y
解:[X] = 010101,[Y] = 111110
[-Y] = 000010
[X]+[-Y] = 010111
求补得到:
X-Y = +10111定点数减法器设计
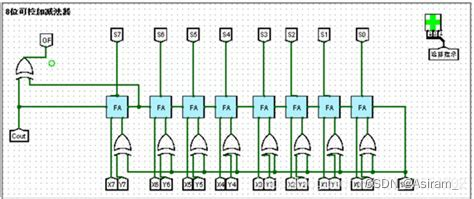
根据定点数补码减法可以基于加法器设计减法器:
其中A的各位输入不变,但是B的输入相比加法器有变化,因为要转化成对应的-Y。注意右下角的原件。当遇见第一个1以前,右下角原件的值为0,即Y各位按原来的值输入;遇见第一个1之后,右下角原件的值为1,即Y的各位取反输入。
阵列加减法,串行和并行运算
根据上面的结构我们知道,一个ALU是由全加器串接组成的。那么我们可以用相同的方法实现阵列加法。
例如,假设我们要计算一个32位的加法,我们就可以使用4个8位加法器串接组成。这种结构叫做串行结构。
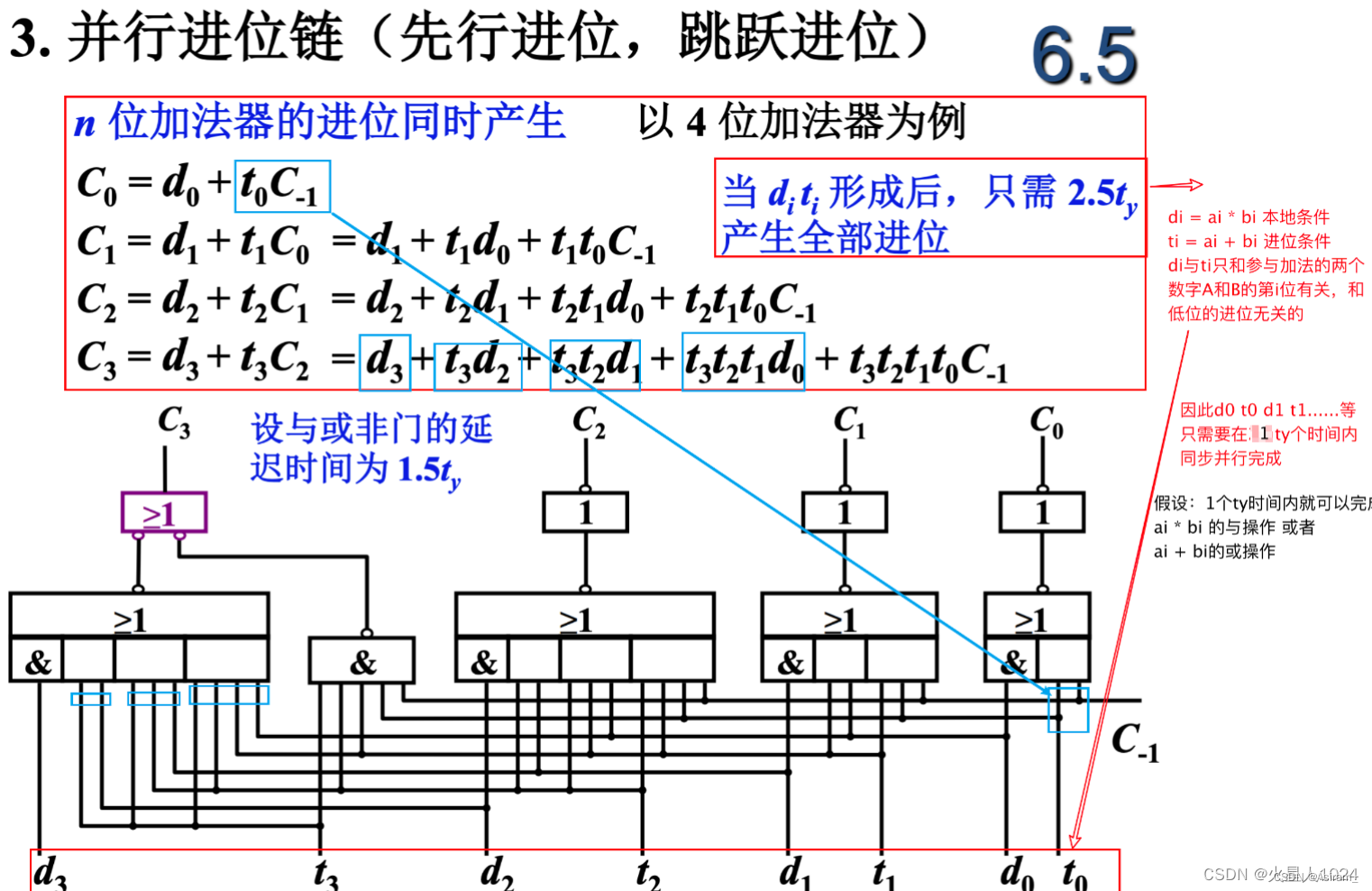
但是串行结构有一个缺点:后面的FA的运算必须等待前一个FA运算完才能执行。这个方法在数据量较大的时候效率会显得很低。因此我们可以采用另外一种方法:并行进位。
根据上图可以得到:一个ALU的进位位可以直接由上一个ALU的进位和AB输入决定。也就是:
因此就不需要等待多个FA进行计算产生进位,可以首先直接产生该ALU的进位到下一个ALU,这种直接产生进位的加法器就叫并行加法器。但是,在ALU之间,下一个ALU依然需要等待该ALU计算完才能计算。
我们可以进一步,将一个ALU视为一个单元,用每个ALU的
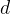
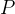
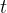
溢出的处理
对于溢出的处理,加法和减法的处理方法不同,需要在进位位设置判断。
- 对于加法来说,有两种情况:负数下溢和正数上溢。根据真值表判断,输入位和输出位异或的结果即为是否溢出。
- 对于减法来说,可以采用双符号位(正数00,负数11进行判断。若计算结果为01,表示发生了上溢,若计算结果为10,表示发生了下溢。
总结
定点数的加减法是乘除法的基础,而定点数减法又基于定点数加法器。其中,加法器基于一位的全加器组成。这种串接的结构在计算中有两种的计算方式:串行计算和并行计算。其中,并行计算效率更高,但是电路相对复杂。