Lecture 6: Gradient Descent
- Basic Knowledge
- Gradient
- Gradient Descent
- Online Gradient Descent
Basic Knowledge 基础知识
Norm and Inner Products 范数与内积
2范数: ∣ ∣ x ⃗ ∣ ∣ = < x ⃗ , x ⃗ > ||\vec{x}|| = \sqrt{<\vec{x},\vec{x}>} ∣∣x∣∣=<x,x>
内积满足数乘和三角不等式:
∣
∣
c
x
⃗
∣
∣
=
∣
c
∣
∣
∣
x
⃗
∣
∣
∣
∣
x
⃗
+
y
⃗
∣
∣
≤
∣
∣
x
⃗
∣
∣
+
∣
∣
y
⃗
∣
∣
||c\vec{x}|| = |c| ||\vec{x}||\\ ||\vec{x}+\vec{y}|| \leq ||\vec{x}|| + ||\vec{y}||
∣∣cx∣∣=∣c∣∣∣x∣∣∣∣x+y∣∣≤∣∣x∣∣+∣∣y∣∣
但是
∣
∣
x
⃗
+
y
⃗
∣
∣
2
=
∣
∣
x
⃗
∣
∣
2
+
∣
∣
y
⃗
∣
∣
2
+
2
<
x
⃗
,
⃗
y
>
||\vec{x}+\vec{y}||^2 = ||\vec{x}||^2+||\vec{y}||^2 + 2<\vec{x}\vec,{y}>
∣∣x+y∣∣2=∣∣x∣∣2+∣∣y∣∣2+2<x,y>
Convexity 凸函数
一般来说,凸指的是如下含义:对于区域 K K K,其中 x x x, y ∈ K y\in K y∈K,如果 ∀ z = a x + ( 1 − a ) y , ( a ∈ [ 0 , 1 ] ) , z ∈ K \forall z = ax+(1-a)y, (a\in[0,1]), z\in K ∀z=ax+(1−a)y,(a∈[0,1]),z∈K,那么我们就说 K K K是凸的。
同样的,如果对于一个函数,其函数图像上两点连成的线段都在这个函数图像的上方,那么我们就说这个函数是一个凸函数,否则是一个凹函数。也就是: f ( λ x + ( 1 − λ ) y ) ≤ λ f ( x ) + ( 1 − λ ) f ( y ) f(\lambda x+(1-\lambda)y) \leq \lambda f(x)+(1-\lambda)f(y) f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)
在微积分中,我们曾经提到过,一元函数是凸函数的条件是其二阶导数大于0,也就是 d 2 f ( x ) d x 2 > 0 \frac{d^2f(x)}{dx^2}>0 dx2d2f(x)>0。
如果函数是多元函数,那么就涉及偏微分的概念。这个时候可微多元函数是凸函数的判定就变为:
f
(
y
)
≥
f
(
x
)
+
<
∇
f
(
x
)
,
y
−
x
>
f(y)\geq f(x)+<\nabla f(x),y-x>
f(y)≥f(x)+<∇f(x),y−x>
这里的
∇
f
(
x
)
\nabla f(x)
∇f(x)就是函数的梯度。
Gradient 梯度
梯度(gradient)的定义如下:
∇
f
(
x
)
=
(
∂
f
∂
x
1
,
…
,
∂
f
∂
x
n
)
\nabla f(\bold{x}) =(\frac{\partial f}{\partial x_1},\dots,\frac{\partial f}{\partial x_n})
∇f(x)=(∂x1∂f,…,∂xn∂f)
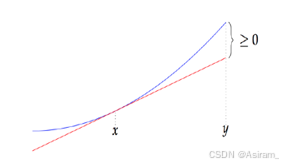
有了梯度的概念,理解上面多元凸函数的判定也不难,大致就是一个线性估计法,如下图所示:
Gradient Descent 梯度下降法
由于梯度是偏导数组成的向量,那么求多元函数极值的时候,只需要找到梯度等于0的点就可以了。这个结论为梯度下降法提供了依据。
但是多元函数的情况比较复杂,直接设 ∇ f ( x ) = 0 \nabla f(x) = \bold{0} ∇f(x)=0去求解析解一般是非常困难的。所以我们采用一种方法逐步减少梯度直至其达到可以认定为0的程度,这种方法叫做梯度下降法。
梯度下降法的基本框架如下:
- 选取一个基本点 x 0 \bold{x_0} x0和步数 T T T
- 在每一步执行如下操作:
x
t
+
1
←
x
t
−
η
t
⋅
∇
f
(
x
t
)
x_{t+1}\larr x_t - \eta_t \cdot\nabla f(\bold{x}_t)
xt+1←xt−ηt⋅∇f(xt)
得到下一步的迭代点
x
t
+
1
\bold{x}_{t+1}
xt+1
3. 最后返回
x
^
=
1
T
Σ
t
=
0
T
−
1
x
t
\hat{\bold{x}} = \frac{1}{T}\Sigma_{t=0}^{T-1}\bold{x}_t
x^=T1Σt=0T−1xt
其中 η t \eta_t ηt被称作“学习度”。
在每一次迭代中,我们向梯度方向的反方向移动来减少损失函数。
在实际操作中,实际上很多时候会直接输出迭代结果 x t \bold{x}_t xt,但是用于证明时则更多使用 x ^ \hat{\bold{x}} x^,因此这里最终返回 x ^ \hat{\bold{x}} x^。
Gradient Descent Convergence 梯度下降法的收敛性
下面我们证明:上面的方法对于所有凸函数是收敛的。也就是,如果评估函数是一个凸函数,梯度下降法不会陷入无限迭代,一定会最终接近目标点。
我们假定 D = ∣ ∣ x 0 − x ∗ ∣ ∣ D = ||\bold{x}_0-\bold{x}^*|| D=∣∣x0−x∗∣∣是起始点到目标点的距离。
然后,我们指定一个上界 G G G,使得我们所有的 x \bold{x} x均满足 ∣ ∣ ∇ f ( x ) ∣ ∣ ≤ G ||\nabla f(\bold{x})||\leq G ∣∣∇f(x)∣∣≤G。
定理表述如下:对于任何可微凸函数
f
:
R
n
→
R
f:\R^n \rarr \R
f:Rn→R,和任何起始点
x
0
x_0
x0,如果我们令
T
=
(
G
D
ϵ
)
2
T = (\frac{GD}{\epsilon})^2
T=(ϵGD)2,$\eta_t =\eta = \frac{D}{G\sqrt{T}} $,那么有
f
(
x
^
)
−
f
(
x
∗
)
≤
ϵ
f(\hat{\bold{x}})-f(\bold{x}^*) \leq \epsilon
f(x^)−f(x∗)≤ϵ
其中 D , G D,G D,G需要我们尝试不同的学习率 η \eta η和步数 T T T间接得出。
上面的定理被称作基本梯度下降 Basic Gradient Descent,下面我们证明其加强定理在线梯度下降Online Gradient Descent.
Online Gradient Descent 在线梯度下降
在线梯度下降和基本梯度下降方式像素。在每一轮迭代,算法使用当前时刻损失函数的梯度更新模型。也就是原来式子中的 f f f变成了 f t f_t ft。
下面我们证明:
Σ
t
=
0
T
−
1
f
t
(
x
t
)
≤
Σ
t
=
0
T
−
1
f
t
(
x
∗
)
+
η
2
G
2
T
+
1
2
η
D
2
\Sigma_{t=0}^{T-1}f_t(\bold{x}_t) \leq \Sigma_{t=0}^{T-1}f_t(x^*) + \frac{\eta}{2}G^2T + \frac{1}{2\eta}D^2
Σt=0T−1ft(xt)≤Σt=0T−1ft(x∗)+2ηG2T+2η1D2
这个式子左边可以简写成 1 T Σ x f ( x t ) \frac{1}{T}\Sigma_xf(x_t) T1Σxf(xt),由于是凸函数,因此其大于 f ( x ^ ) f(\hat{x}) f(x^),而右边可以简写为 f ( x ∗ ) + ϵ f(x^*)+\epsilon f(x∗)+ϵ。
我们使用一个潜力函数来证明上面定理。
- 定义潜力函数
Φ
t
=
∣
∣
x
t
−
x
∗
∣
∣
2
2
η
\Phi_t = \frac{||\bold{x_t}-\bold{x^*}||^2}{2\eta}
Φt=2η∣∣xt−x∗∣∣2
那么有
Φ
0
=
1
2
η
D
2
\Phi_0 = \frac{1}{2\eta}D^2
Φ0=2η1D2
那么原定理告诉我们:
Σ
f
t
(
x
t
)
≤
Σ
f
t
(
x
∗
)
+
η
2
G
2
T
+
1
2
η
D
2
\Sigma f_t(x_t) \leq \Sigma f_t(x^*) + \frac{\eta}{2}G^2T + \frac{1}{2\eta }D^2
Σft(xt)≤Σft(x∗)+2ηG2T+2η1D2
又因为:
D
2
=
−
Σ
∣
∣
x
t
+
1
−
x
∗
∣
∣
2
+
Σ
∣
∣
x
t
−
x
∗
∣
∣
2
D^2 = - \Sigma||\bold{x_{t+1}}-\bold{x^*}||^2 + \Sigma||\bold{x_{t}}-\bold{x^*}||^2
D2=−Σ∣∣xt+1−x∗∣∣2+Σ∣∣xt−x∗∣∣2
因此我们两边把求和拆开,我们只需要证明:
如下命题
f
t
(
x
t
)
+
(
Φ
t
+
1
−
Φ
t
)
≤
f
t
(
x
∗
)
+
η
2
G
2
f_t(x_t) + (\Phi _{t+1} - \Phi_t) \leq f_t(x^*) + \frac{\eta}{2}G^2
ft(xt)+(Φt+1−Φt)≤ft(x∗)+2ηG2
由于
(
Φ
t
+
1
−
Φ
t
)
=
1
2
η
(
∣
∣
x
t
+
1
−
x
∗
∣
∣
2
+
∣
∣
x
t
−
x
∗
∣
∣
2
)
=
1
2
η
(
∣
∣
x
t
+
1
−
x
t
∣
∣
2
+
2
<
x
t
+
1
−
x
t
,
x
t
−
x
∗
>
)
=
1
2
η
(
∣
∣
∇
f
t
(
x
t
)
∣
∣
2
−
2
η
<
∇
f
t
(
x
t
)
,
x
t
−
x
∗
>
)
≤
η
2
G
2
−
<
∇
f
t
(
x
t
)
,
x
t
−
x
∗
>
(\Phi _{t+1} - \Phi_t) = \frac{1}{2\eta}(||\bold{x_{t+1}}-\bold{x^*}||^2 + ||\bold{x_{t}}-\bold{x^*}||^2)\\ = \frac{1}{2\eta}(||\bold{x_{t+1}}-\bold{x_t}||^2 + 2<\bold{x_{t+1}}-\bold{x_t},\bold{x_t}-\bold{x^*}>)\\ =\frac{1}{2\eta}(||\nabla f_t(\bold{x_t})||^2 - 2\eta<\nabla f_t(\bold{x_t}),\bold{x_t}-\bold{x^*}>)\\ \leq \frac{\eta}{2}G^2 - <\nabla f_t(\bold{x_t}),\bold{x_t}-\bold{x^*}>
(Φt+1−Φt)=2η1(∣∣xt+1−x∗∣∣2+∣∣xt−x∗∣∣2)=2η1(∣∣xt+1−xt∣∣2+2<xt+1−xt,xt−x∗>)=2η1(∣∣∇ft(xt)∣∣2−2η<∇ft(xt),xt−x∗>)≤2ηG2−<∇ft(xt),xt−x∗>
又因为凸函数的特性有
f
t
(
x
t
)
−
f
t
(
x
∗
)
≤
<
∇
f
t
(
x
t
)
,
x
t
−
x
∗
>
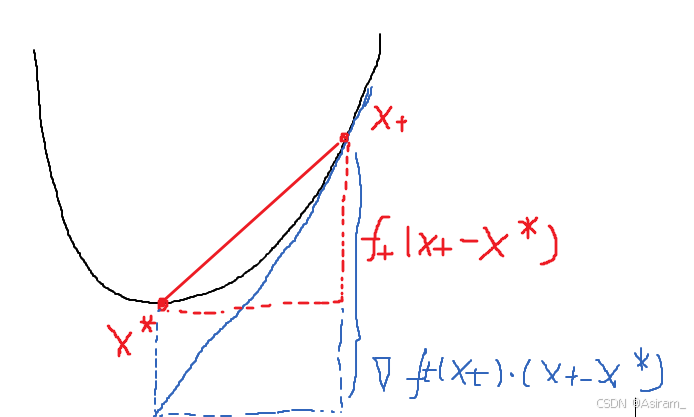
f_t(x_t) - f_t(x^*) \leq <\nabla f_t(\bold{x_t}),\bold{x_t}-\bold{x^*}>
ft(xt)−ft(x∗)≤<∇ft(xt),xt−x∗>
(p.s.:见下图)
因此原命题得证,我们就证明了在线梯度下降定理。
在线梯度下降的定理是一个基本定理,但是在线梯度下降的方法是什么呢?
Extra: What is Online Gradient Descent
梯度下降法是一种以线性方式逼近最优点的方法。而OGD(在线梯度下降)和SGD(普通梯度下降)的区别在于其目标函数也是变化的。因此其根据每步收到的数据就能进行梯度下降,而不是像普通的梯度下降,必须收到所有的数据知道 f f f之后才能进行梯度下降。