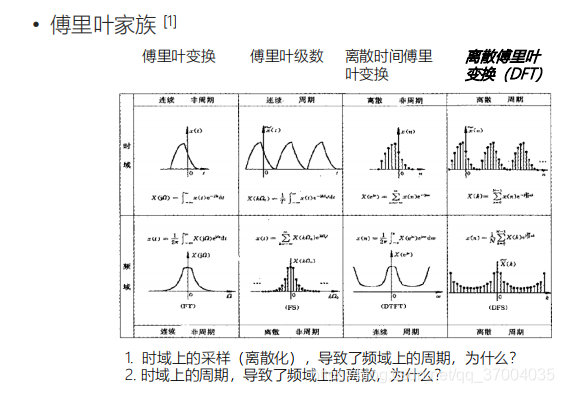
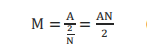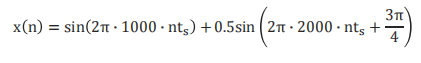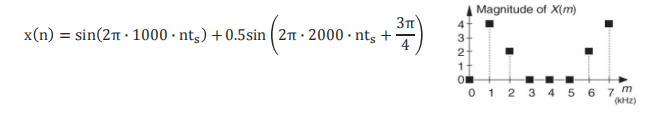语音信号处理以及特征提取
数字信号处理

1. 模拟信号到数字信号的转化(ADC)
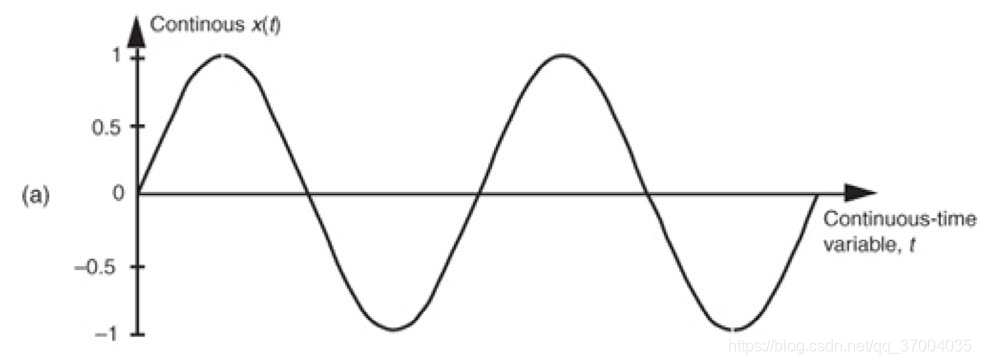
   很简单了，就是计算机识别的是数字信号，而语音信号是连续信号，所以需要对连续的语音模拟信号进行采样，量化，转换成数字信号，如下图所示：
   
   
2. 基础定义
   正弦波的定义是：$x(t)=sin(2\pi f_{0}t)$ 其中$f_0$代表的是频率，单位时间内周期震动的次数，单位是HZ。
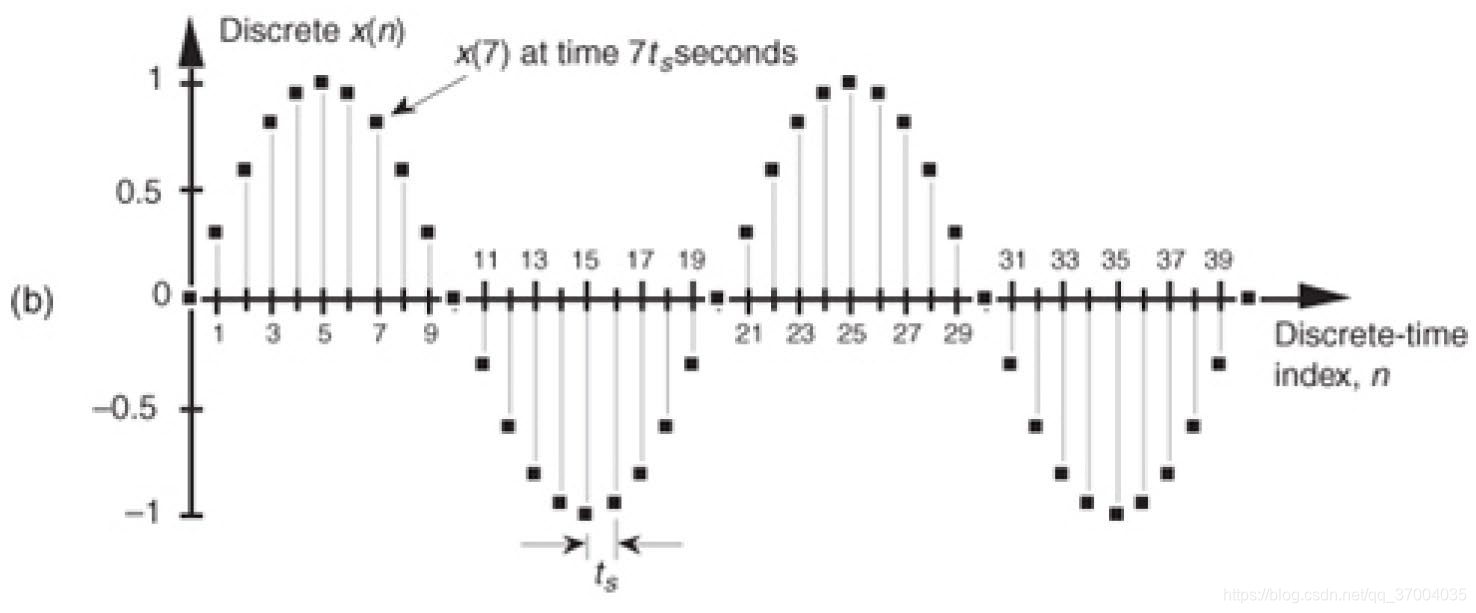
   如果我们对此正弦波进行采样，每隔 $t_s$ 秒进行一次采样，并使用一定范围的离散数值表示采样值，则可以得到采样后的离散信号(b）可以得到：
   $x(n)=sin(2\pi f_{0}n{t}_s)$
   注意： $t_s$ 是采样周期
   $f_s=\frac{1}{t_s}$为采样频率，或采样率，表示1s内采样的点数。
   n = 0,1, … … 为离散整数序列
   
3. 频率混叠
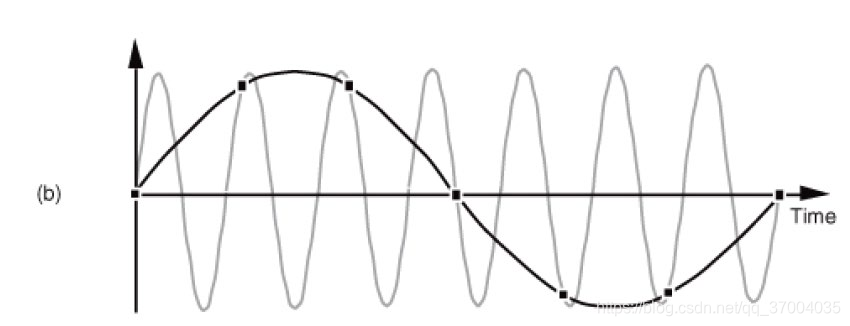
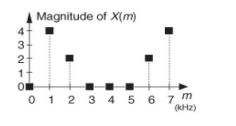
     什么是频率混叠呢？也就是说不同频率的正弦波，经过采样后会出现完全相同的离散信号；
   
   

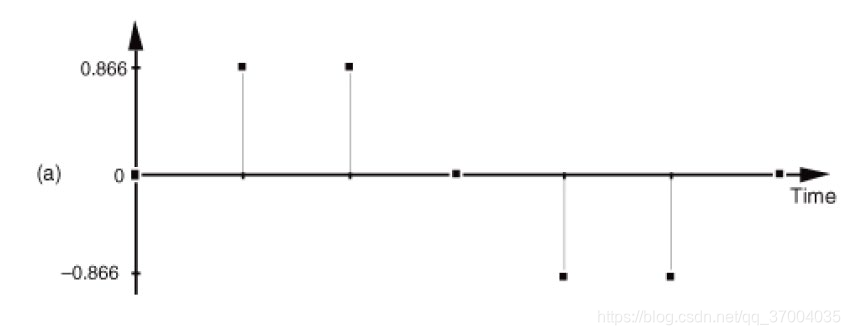
图a是采集的数字信号，但是在图b中出现了两个频率不同的连续信号。下面我们用公式解释一下：
$$\begin{array}{c}x(n)=sin(2\pi f_{0}n{t}_s)\\ =sin(2\pi f_{0}n{t}_s+2\pi m)\\ =sin(2\pi (f_0+\frac{m}{n{t}_s})n{t}_s)\end{array}$$
其中$m=kn,n=0.1.2...$离散整数数列，所以上述公式可以写为：$sin(2\pi (f_0+k{f}_s)n{t}_s)$故，会出现多个不同频率的正弦函数。
怎么解决频率混叠的问题呢？

我们所用的就是奈奎斯特采样定律
采样频率大于信号中最大频率的两倍！
$$\frac{f_s}{2}\ge f_{max}$$
$f_s$是采样频率$f_{max}$是原始连续的语音模拟信号：
即，在原始信号的一个周期内，至少要采样两个点，才能有效杜绝频率混叠问题。

4. 傅里叶变换
   为什么需要傅里叶变换呢？
   将时域信号转换成频域信号，以此来分析信号中频域中的成分；
   什么信号可以进行傅里叶变换呢？
   时域离散且周期的信号，其中，非周期信号需要进行周期延拓才能进行傅里叶变化；
   
   在傅里叶家族 中，能够被计算机所用到的就是离散傅里叶变换（DFT），只有DFT是在时域和频域上都具有离散和周期的特点，因此，也只有DFT可以用计算机来处理！

点击查看傅里叶频域和时域关系的详细解答
傅里叶变换公式：


DFT的性质：

其中$X^{\ast }$代表的是共轭复数，点击查看共轭复数

性质2：谱密度：
什么是谱密度呢？
傅里叶变换后的X(m)实际上表示的是“谱密度”（spectral density），如果对一个幅度为A实正弦波进行N点DFT，则DFT之后，对应频率上的幅度M和A之间的关系为：

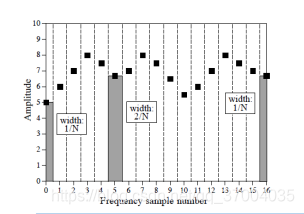
其中$2/N$表示的是一个单位频率下的宽度，如下图所示：

其实表示的就是，在单位频率之下，所拥有的能量是多少，DFT之后的频域序列X(m)的幅值实际上是一个“密度”的概念，通俗讲，即单位带宽上有多少信号存在。
对于谱密度，我们可以用一个例子来进行验证：

像上面的这个公式，$x(n)$是由两个正弦函数组成的，其中第一个正弦函数的A（幅度）是1，第二个正弦函数的幅度A是0.5；如图所示：

N是8，则$A_{1}N/2=4,A_{2}N/2=2$ 谱密度正好对应的就是$x(m)$的值；
性质3：DFT的线性；

什么是DFT的频率轴？
频率分辨率：$f_s/N$表示最小的频率间隔，当N越大时，频率分辨率越高。
**分析频率：**在频域上，第m个点所表示的分析频率为：
$f_{analysis}(m)=\frac{m}{n}{f}_s$
其$f_s=1/t_s$,为采样频率，或采样率，表示1s内采样的
点数，
举个例子：

在上图中，$f_s=8000,n=8$则当$m=1$时，即为$f_{analysis}=1000,当m=2时，f_{analysis}=2000$分别对应于$x(n)$中的第一和 第二个频率大小；
我们可以理解为X(m)的幅值，体现了原信号中频率成分为$\frac{m}{n}{f}_s$HZ 的信号的强度

为了提高DFT频率轴的分辨率，而不会影响原始信号的频率成分。我们可以将时域长度为N的信号x(n) 补0，增加信号的长度，从而提高频率轴分辨率。
对信号进行补0的操作，不会影响DFT的结果，这在FFT（快速傅里叶变换）中和语音信号分析中非常常见。比如，在语音特征提取阶段，对于16k采样率的信号，一帧语音信号长度为400个采样点，为了进行512点的FFT，通常将400个点补0，得到512个采样点，最后只需要前257个点。
快速傅里叶变换（FFT）
闲的时候再看吧，跟的这个课程没有详细讲解，但是FFT还是非常重要的，以后再补；
接下来就开始进入语音识别的世界吧；
Fbank和MFCC特征提取
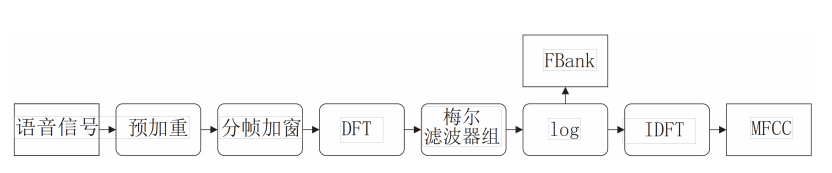
在进行语音识别的过程中，首先要做的就是对语音信号进行处理。见下图；

后面会分别进行介绍。
进行这样处理是传统的语音识别处理过程，但是在端到端的语音识别处理的过程中，可以直接就会对语音信号波形进行识别和建模，但是效果并没有超过基于频域的语音信号建模；

1. 预加重
   预加重的目的？
    提高信号高频部分的能量，高频信号在传递过程中，衰减较快，但是高频部分又蕴含很多对语音识别有利的特征，因此，在特征提取部分，需要提高高频部分能量;
   预加重滤波器是一个一阶高通滤波器，给定时域输入信号𝑥[𝑛]，预加重之后的信号为:
   $$y[n]=x[n]-ax[n-1]$$
   其中$0.9\le a\le 1.0$
   由公式可以看出：
   (1)果信号x是低频信号（变化较慢），那么x[n]和 x[n-1] 的值应该很接近，当𝛼在接近1的时候，𝑥[𝑛]−𝛼𝑥[𝑛−1] 接近于0，此信号的幅度将被大大抑制；
   (2)如果x是高频信号（变化很快），那么x[n] 和x[n-1] 的值将相差很大，𝑥[𝑛]−𝛼𝑥[𝑛−1] 的值不会趋近0，此信号的幅度还能保持，可以通过此滤波器;
   

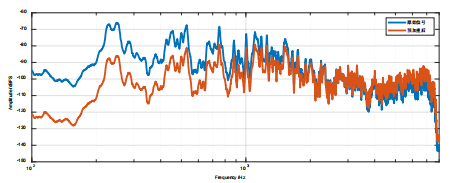
 如上图所示，横轴是频率，纵轴是在此频率下信号的强度，其中红线是预加重之后的，在频率很低的时候，信号强度是低于原始信号的，随着频率的提高，预加重的信号强度是逐渐大于原始信号的；

2. 分帧加窗

为什么要进行分帧呢？
  •语音信号为非平稳信号，其统计属性是随着时间变化的，以汉语为例，一句话中包含很多声母和韵母，不同的拼音，发音的特点很明显是不一样的；
  • 但是！语音信号又具有短时平稳的属性，比如汉语里一个声母或者韵母，往往只会持续几十到几百毫秒，在这一个发音单元里，语音信号表现出明显的稳定性，规律性
  • 在进行语音识别的时候，对于一句话，识别的过程也是以较小的发音单元（音素、字、字节）为单位进行识别，因此用滑动窗来提取短时片段

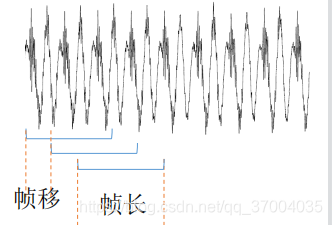
如上图所示，就是帧长和帧移的形象化表示；
例如对于采样率为16kHz的信号，帧长、帧移一般为25ms、10ms，即400和160个采样点（16KHZ代表的是一秒钟采集16000个采样点，所以 16000*0.25=400）

分帧加窗过程
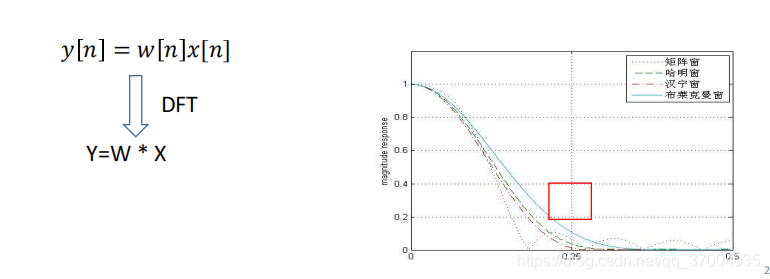
其实很简单，就是分帧的过程，在时域上，即用一个窗函数和原始信号进行相乘：
$$y[n]=w[n]x[n]$$
$w[n]$称为窗函数，常见的窗函数有：

为什么不直接使用矩形框窗呢？
加窗的过程，实际上是在时域上将信号截断，窗函数与信号在时域相乘，就等于对应的频域表示进行卷积（*），矩形窗主瓣窄，但是旁瓣较大（红色部分），将其与原信号的频域表示进行卷积，就会导致频率泄露。