JS实现动态分区分配中的首次适应算法和最佳适应算法

实验目的

了解动态分区分配方式中使用的数据结构和分配算法，并进一步加深对动态分区存储管理方式及其实现过程的理解。

实验内容

(1)

用C语言(不会C这里就用JS实现)分别实现采用首次适应算法和最佳适应算法的动态分区分配过程alloc( )和回收过程free( )。其中，空闲分区通过空闲分区链来管理：在进行内存分配时，系统优先使用空闲区低端的空间。

(2)

假设初始状态下，可用的内存空间为640KB，并有下列的请求序列：

•作业1申请130KB。
•作业2申请60KB。
•作业3申请100KB。
•作业2释放60KB。
•作业4申请200KB。
•作业3释放100KB。
•作业1释放130KB。
•作业5申请140KB。
•作业6申请60KB。
•作业7申请50KB。
•作业6释放60KB。

请分别采用首次适应算法和最佳适应算法，对内存块进行分配和回收，要求每次分配和回收后显示出空闲分区链的情况。

思路解析

1 首先给大家介绍下首次适应算法和最佳适算法

首次适应算法

首次适应算法从空闲分区表的第一个表目起查找该表，把最先能够满足要求的空闲区分配给作业，这种方法目的在于减少查找时间。为适应这种算法，空闲分区表(空闲区链)中的空闲分区要按地址由低到高进行排序。该算法优先使用低址部分空闲区，在低址空间造成许多小的空闲区，在高地址空间保留大的空闲区。

最佳适应算法

它从全部空闲区中找出能满足作业要求的、且大小最小的空闲分区，这种方法能使碎片尽量小。为适应此算法，空闲分区表（空闲区链）中的空闲分区要按从小到大进行排序，自表头开始查找到第一个满足要求的自由分区分配。该算法保留大的空闲区，但造成许多小的空闲区。

上面是百度百科给的定义，其实已经解释的很清楚了，我在这里给大家举一个例子。

比如你有一个数组->[6,4,9,5,2,1],里面的数值分别代表空间吧，这时候你有一个物体，只需要占用2空间。

这时候你使用这个算法，从6开始遍历，发现6大于你需要的空间，那么这个物体肯定是可以存放的，所以你就选用6来存储这个2空间的物体，然后6空间就会成4空间。其实这个4空间就算是一个碎片了

如果你又来了一个需要6空间的物体，然后刚好6空间被你用了(只剩下一个4空间)，那么只好向下找。这个就是首次适应算法。

如果你采用最佳适应算法，那么你需要2空间，它从6开始遍历，然后找到刚刚适合2空间的(或者是距离它并且能装下它的空间)2。这时候就把2空间给占用了。如果你需要4空间，那么5就会被占用，剩下1空间。它的缺点就是，会有很多的小碎片。

2 切入正题题目要求是两种方法来实现对这个作业的调度

作业的调度有申请和释放，空间同时有空闲分区和占用的分区。这就意味着我们需要先定义两个方法和两个数组空间

firstaddress是指该作业的首地址。 lastaddress是该作业的末地址。 length是指长度

let UseQueue = []// 占用的分区
let freeQueue = [{
    firstAddress: 0,
    lastAddress: 640,
    length: 640
}]//空闲的分区  因为首先由640的空间
function free(Progress)//释放过程
function FirstFit(Progress)//首次适应算法 申请
function BestFit(Progress)//最佳适应算法 申请

一共有7个作业，所以我们这里需要先定义一个作业类，然后创建7个作业对象

function PCB(ID, firstAddress, length, lastAddress, flag) {
    this.ID = ID //进程的ID
    this.firstAddress = firstAddress //进程的首地址
    this.length = length //进程的长度
    this.lastAddress = lastAddress //进程的末地址
    this.flag = flag //是否使用
}

//定义七个进程 这里首地址都是0，因为没分配
let one = new PCB(1, 0, 130, 0, 'false')
let two = new PCB(2, 0, 60, 0, 'false')
let three = new PCB(3, 0, 100, 0, 'false')
let four = new PCB(4, 0, 200, 0, 'false')
let five = new PCB(5, 0, 140, 0, 'false')
let six = new PCB(6, 0, 60, 0, 'false')
let seven = new PCB(7, 0, 50, 0, 'false')

先编写一个有用的排序算法，后面会用的到，是利用一个对象中的某个属性进行排序

function sortlastAddressy(field) {
    return function(a, lastAddress) {
        return a[field] - lastAddress[field];
    }
}

这里实现首次适应算法

Progress就是指各个作业比如one作业上面已经定义了，每次进入一个作业
首先对空闲队列里面的空间进行排序(按照首地址排，并不是按照空间的大小排序，按照空间大小排那就是最佳适应算法了)。
然后对空闲队列进行遍历，找到第一个适应Progress长度的空间，然后分配给它。
里面的各个参数我进入代码给你们解释，看代码！

function FirstFit(Progress) {
    Progress.flag = "true"
    let d //它用来记录每次是空闲区间中哪一块被使用，记录它的末地址
    freeQueue.sort(sortlastAddressy("firstAddress"));//利用首地址排序，
    for (let i = 0; i < freeQueue.length; i++) {
        if (freeQueue[i].length > Progress.length) {
            Progress.firstAddress = freeQueue[i].firstAddress
            d = freeQueue[i].lastAddress
            break;//找到以后就退出循环，不在遍历 找到了还遍历个逑啊
        }
    }
    /*
    firstaddress 是我在全局定义的一个变量，用来记录每次在空闲去 生成空闲块的首地址
    比如200-400的空闲   然后作业需要100空间，这里的Progress.firstAddress都是0，因为没有
    被分配，所以都是0，那么firstaddress=100 ，分配以后，剩下的空闲块的首地址就是100了
    
    */
    firstAddress = Progress.firstAddress + Progress.length
    Progress.lastAddress = Progress.firstAddress + Progress.length
    UseQueue.push(Progress)//当作业被申请以后，就要进入占用空间
    /*定义空闲块的末地址，也就是被使用的空闲块的末地址，200-400
    被占用100以后 400还是是末地址   剩下的就是300-400的空闲块/*
    let lastAddress = d 
    let length = lastAddress - firstAddress
    //每次分配作业以后就把 空闲块装进空闲空间
    freeQueue.push({
        firstAddress,
        lastAddress,
        length,
    })
}

这里实现最佳适应算法

这里和首次适应算法的流程一样，区别就是排序的时候，这里是使用长度排序，而不是首地址
空闲区里面第一个就是长度就短了，那么每次遍历只需要从头开始，找到第一个适合自己的，就是那个最适合自己的空间，然后退出，发现自己太聪明了。

function BestFit(Progress) {
    Progress.flag = "true"
    let d
    freeQueue.sort(sortlastAddressy("length"));
    for (let i = 0; i < freeQueue.length; i++) {
        if (freeQueue[i].length > Progress.length) {
            Progress.firstAddress = freeQueue[i].firstAddress
            d = freeQueue[i].lastAddress
            break;
        }
    }
    firstAddress = Progress.firstAddress + Progress.length
    Progress.lastAddress = Progress.firstAddress + Progress.length
    UseQueue.push(Progress)
    let lastAddress = d
    let length = lastAddress - firstAddress
    freeQueue.push({
        firstAddress,
        lastAddress,
        length
    })
}

这里实现释放算法

每次释放，作业就不是调用状态，就把它的状态改为false
详细解析看代码

function free(Progress) {
    Progress.flag = 'false'
    //找到要释放的作业的位置
    let index = UseQueue.indexOf(Progress)
    //把该作业删除
    UseQueue.splice(index, 1)
    /* 
    同时记录该作业的首地址，末地址，长度
    因为他们释放以后，他们占用的空间就会变成空闲的，把该空闲块放到空闲空间中
    */
    let firstAddress = Progress.firstAddress
    let lastAddress = Progress.firstAddress + Progress.length
    let length = lastAddress - firstAddress
    freeQueue.push({
        firstAddress,
        lastAddress,
        length
    })
}

这里实现对空闲空间的操作

里面的内容众多for循环，你先看的话，你肯定不明白什么意思，这里给你说下它的功能你就知道它的代码意思。
这里是因为空闲空间的要求，需要对空间内的碎片进行整合
比如空闲空间有两个空闲块分别是100-200 200-300 你发现第一块的末地址与第二块的首地址相同，你就需要把它们合并成为100-300，这就就剩下一个长度为200的大的空闲块
同时如果是100-400 300-400 这样的空闲块你需要把第一块给删除了，因为100-300被使用。这样就只剩下300-400一块空闲。

function dealFreequeue(freeQueue) {
    if (freeQueue.length > 1) {
        for (let i = 0; i < freeQueue.length; i++) {
            for (let j = 0; j < freeQueue.length; j++) {
                if (freeQueue[i].lastAddress == freeQueue[j].lastAddress && i != j) {
                    if (freeQueue[i].firstAddress > freeQueue[j].firstAddress) {
                        freeQueue.splice(j, 1)
                    } else {
                        freeQueue.splice(i, 1)
                    }

                }

            }
        }

        for (let i = 0; i < freeQueue.length; i++) {
            for (let j = 0; j < freeQueue.length; j++) {
                if (freeQueue[i].lastAddress == freeQueue[j].firstAddress && freeQueue[i] != undefined) {
                    freeQueue[i].lastAddress = freeQueue[j].lastAddress
                    freeQueue[i].length = freeQueue[i].lastAddress - freeQueue[i].firstAddress
                    freeQueue.splice(j, 1)
                    break;
                }
            }
        }
    }
    freeQueue.sort(sortlastAddressy("firstAddress"));
    return freeQueue
}

定义七个作业的执行数组

index=1表示作业申请 index=-1 表示作业释放

let runqueue = [{
        index: 1,
        Progress: one
    },
    {
        index: 1,
        Progress: two
    },
    {
        index: 1,
        Progress: three
    }, {
        index: -1,
        Progress: two
    }, {
        index: 1,
        Progress: four
    }, {
        index: -1,
        Progress: three
    }, {
        index: -1,
        Progress: one
    }, {
        index: 1,
        Progress: five
    }, {
        index: 1,
        Progress: six
    }, {
        index: 1,
        Progress: seven
    }, {
        index: -1,
        Progress: six
    }
]

实现展示界面

function show(freeQueue) {
    let str = ""
    let str1 = "";
    for (item of freeQueue) {
        str = item.firstAddress + "            " + item.lastAddress + "            " + item.length + "\n"
        str1 += str
    }
    console.log("首地址         末地址          长度")
    console.log(str1)

}

实现首次适应算法的执行函数

function FirstFitMain(runqueue) {
    for (item of runqueue) {
        console.log(">>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>")
        if (item.index == 1) {
            console.log("申请-------->", "ID:", item.Progress.ID, "长度:", item.Progress.length)
            FirstFit(item.Progress)
        } else {
            console.log("释放-------->", "ID:", item.Progress.ID, "首地址:", item.Progress.firstAddress, "长度:", item.Progress.length)
            free(item.Progress)

        }
        freeQueue = dealFreequeue(freeQueue)
        console.log("空闲的空间:")
        show(freeQueue)

        console.log("已被占用的空间:")
        console.log(UseQueue)
    }
}

实现最佳适应算法的执行函数

function BestFitMain(runqueue) {
    for (item of runqueue) {
        console.log(">>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>")
        if (item.index == 1) {
            console.log("申请-------->", "ID:", item.Progress.ID, "长度:", item.Progress.length)
            BestFit(item.Progress)
        } else {
            console.log("释放-------->", "ID:", item.Progress.ID, "首地址:", item.Progress.firstAddress, "长度:", item.Progress.length)
            free(item.Progress)
        }
        freeQueue = dealFreequeue(freeQueue)
        console.log("空间的空间:")
        show(freeQueue)
        console.log("已被占用的空间:")
        console.log(UseQueue)
    }
}

调用函数

不使用哪一个算法，就把它注释掉

//FirstFitMain(runqueue)
BestFitMain(runqueue)

详细代码

/*
 * @Author: mikey.zhaopeng 
 * @Date: 2018-12-08 00:20:04 
 * @Last Modified by:   mikey.zhaopeng 
 * @Last Modified time: 2018-12-08 00:20:04 
 */
function PCB(ID, firstAddress, length, lastAddress, flag) {
    this.ID = ID //进程的ID
    this.firstAddress = firstAddress //进程的首地址
    this.length = length //进程的长度
    this.lastAddress = lastAddress //进程的末地址
    this.flag = flag //是否使用
}
//定义七个进程
let one = new PCB(1, 0, 130, 0, 'false')
let two = new PCB(2, 0, 60, 0, 'false')
let three = new PCB(3, 0, 100, 0, 'false')
let four = new PCB(4, 0, 200, 0, 'false')
let five = new PCB(5, 0, 140, 0, 'false')
let six = new PCB(6, 0, 60, 0, 'false')
let seven = new PCB(7, 0, 50, 0, 'false')

let freeQueue = [{
    firstAddress: 0,
    lastAddress: 640,
    length: 640
}]
let UseQueue = []
let firstAddress = 0
    //
function sortlastAddressy(field) {
    return function(a, lastAddress) {
        return a[field] - lastAddress[field];
    }
}

function FirstFit(Progress) {
    Progress.flag = "true"
    let d
    freeQueue.sort(sortlastAddressy("firstAddress"));
    for (let i = 0; i < freeQueue.length; i++) {
        if (freeQueue[i].length > Progress.length) {
            Progress.firstAddress = freeQueue[i].firstAddress
            d = freeQueue[i].lastAddress
            break;
        }
    }
    firstAddress = Progress.firstAddress + Progress.length
    Progress.lastAddress = Progress.firstAddress + Progress.length
    UseQueue.push(Progress)
    let lastAddress = d
    let length = lastAddress - firstAddress
    freeQueue.push({
        firstAddress,
        lastAddress,
        length,
    })
}

function free(Progress) {
    Progress.flag = 'false'
    let index = UseQueue.indexOf(Progress)
    UseQueue.splice(index, 1)
    let firstAddress = Progress.firstAddress
    let lastAddress = Progress.firstAddress + Progress.length
    let length = lastAddress - firstAddress
    freeQueue.push({
        firstAddress,
        lastAddress,
        length
    })
}

function BestFit(Progress) {
    Progress.flag = "true"
    let d
    freeQueue.sort(sortlastAddressy("length"));
    for (let i = 0; i < freeQueue.length; i++) {
        if (freeQueue[i].length > Progress.length) {
            Progress.firstAddress = freeQueue[i].firstAddress
            d = freeQueue[i].lastAddress
            break;
        }
    }
    firstAddress = Progress.firstAddress + Progress.length
    Progress.lastAddress = Progress.firstAddress + Progress.length
    UseQueue.push(Progress)
    let lastAddress = d
    let length = lastAddress - firstAddress
    freeQueue.push({
        firstAddress,
        lastAddress,
        length
    })
}
let runqueue = [{
        index: 1,
        Progress: one
    },
    {
        index: 1,
        Progress: two
    },
    {
        index: 1,
        Progress: three
    }, {
        index: -1,
        Progress: two
    }, {
        index: 1,
        Progress: four
    }, {
        index: -1,
        Progress: three
    }, {
        index: -1,
        Progress: one
    }, {
        index: 1,
        Progress: five
    }, {
        index: 1,
        Progress: six
    }, {
        index: 1,
        Progress: seven
    }, {
        index: -1,
        Progress: six
    }
]

function dealFreequeue(freeQueue) {
    if (freeQueue.length > 1) {
        for (let i = 0; i < freeQueue.length; i++) {
            for (let j = 0; j < freeQueue.length; j++) {
                if (freeQueue[i].lastAddress == freeQueue[j].lastAddress && i != j) {
                    if (freeQueue[i].firstAddress > freeQueue[j].firstAddress) {
                        freeQueue.splice(j, 1)
                    } else {
                        freeQueue.splice(i, 1)
                    }

                }

            }
        }

        for (let i = 0; i < freeQueue.length; i++) {
            for (let j = 0; j < freeQueue.length; j++) {
                if (freeQueue[i].lastAddress == freeQueue[j].firstAddress && freeQueue[i] != undefined) {
                    freeQueue[i].lastAddress = freeQueue[j].lastAddress
                    freeQueue[i].length = freeQueue[i].lastAddress - freeQueue[i].firstAddress
                    freeQueue.splice(j, 1)
                    break;
                }
            }
        }
    }
    freeQueue.sort(sortlastAddressy("firstAddress"));
    return freeQueue
}

function FirstFitMain(runqueue) {
    for (item of runqueue) {
        console.log(">>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>")
        if (item.index == 1) {
            console.log("申请-------->", "ID:", item.Progress.ID, "长度:", item.Progress.length)
            FirstFit(item.Progress)
        } else {
            console.log("释放-------->", "ID:", item.Progress.ID, "首地址:", item.Progress.firstAddress, "长度:", item.Progress.length)
            free(item.Progress)

        }
        freeQueue = dealFreequeue(freeQueue)
        console.log("空闲的空间:")
        show(freeQueue)

        console.log("已被占用的空间:")
        console.log(UseQueue)
    }
}

function BestFitMain(runqueue) {
    for (item of runqueue) {
        console.log(">>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>")
        if (item.index == 1) {
            console.log("申请-------->", "ID:", item.Progress.ID, "长度:", item.Progress.length)
            BestFit(item.Progress)
        } else {
            console.log("释放-------->", "ID:", item.Progress.ID, "首地址:", item.Progress.firstAddress, "长度:", item.Progress.length)
            free(item.Progress)
        }
        freeQueue = dealFreequeue(freeQueue)
        console.log("空间的空间:")
        show(freeQueue)
        console.log("已被占用的空间:")
        console.log(UseQueue)
    }
}

function show(freeQueue) {
    let str = ""
    let str1 = "";
    for (item of freeQueue) {
        str = item.firstAddress + "            " + item.lastAddress + "            " + item.length + "\n"
        str1 += str
    }
    console.log("首地址         末地址          长度")
    console.log(str1)

}
//FirstFitMain(runqueue)
BestFitMain(runqueue)

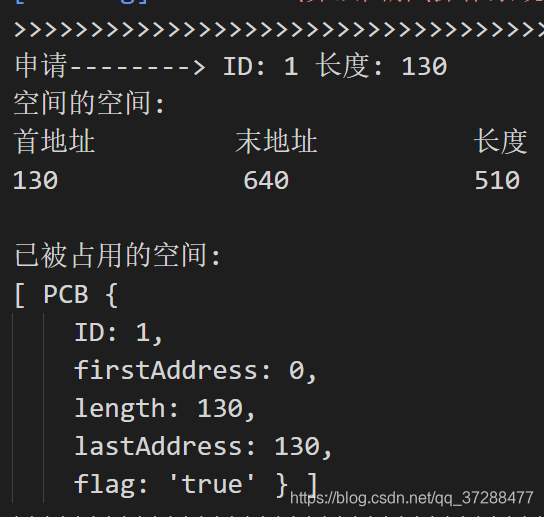
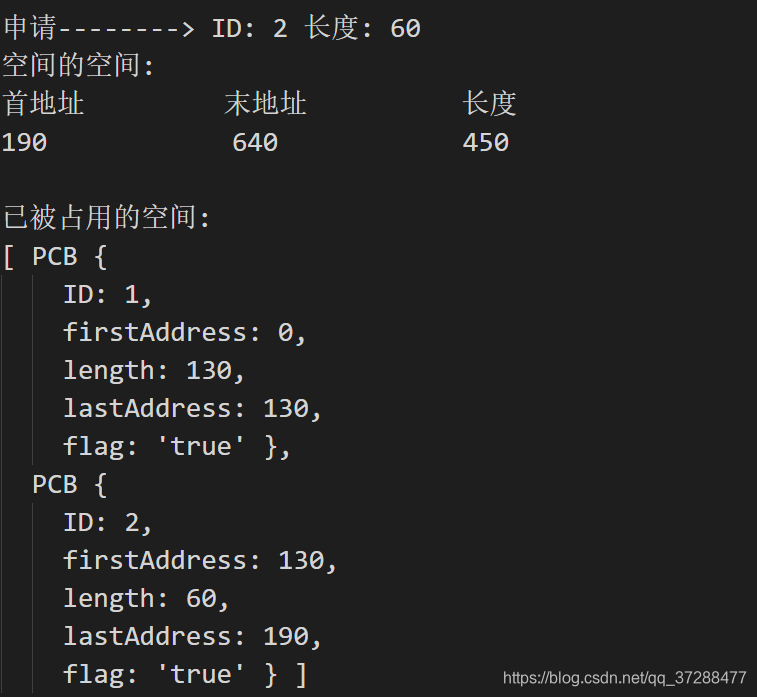
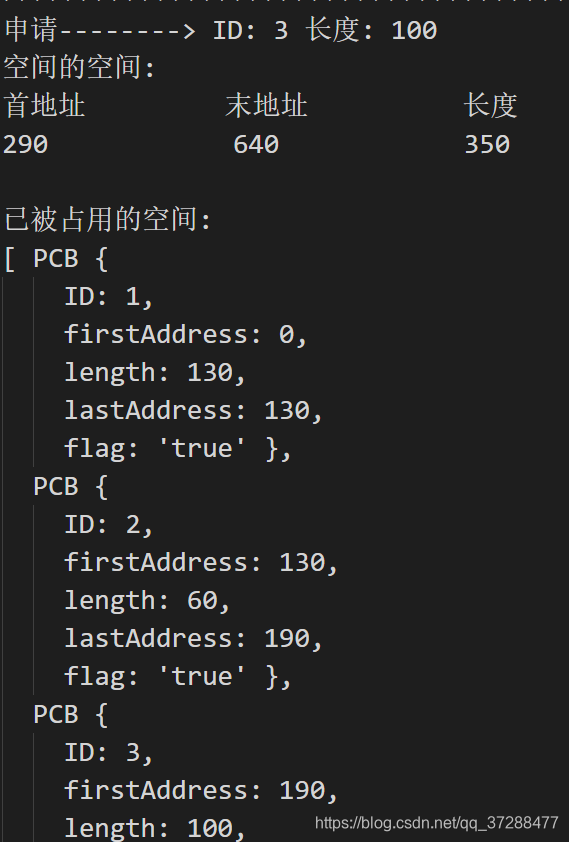
给大家看下结果，这里就截几个图，并不是全部结果，就前三个
在这里插入图片描述