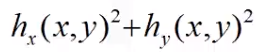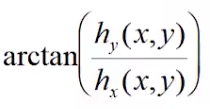原视频教程:
https://www.bilibili.com/video/BV19x411X7k6?from=search&seid=9816644268076164289
一、颜色特征
1.1、量化颜色直方图
在第二节中提到过灰度图,把HSV的所有颜色都列出来,然后按灰度直方图的方式来统计图片中的每一个像素点,得到的图形就是量化颜色直方图。
适用于:HSV空间
优点:计算高效(直接统计即可)
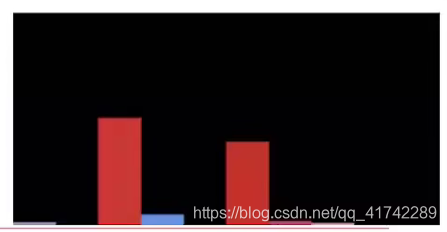
缺点:分布稀疏,色彩简单的图像进行量化颜色后,有可能直方图的大部分HSV色值都没有点分布,如下图:
1.2、聚类颜色直方图
先对颜色进行聚类,形成每一个单元(bin,即聚类中心),聚类后得到每个bin色值,作为直方图的横坐标。
此时对原图进行转换,将用聚类中心的bin代表该聚类中的所有元素,如下图:
再进行直方图计算:
适用于:Lab空间
下面这个没看懂
二、几何特征
2.1、Edge 边缘
2.1.1 数学推导
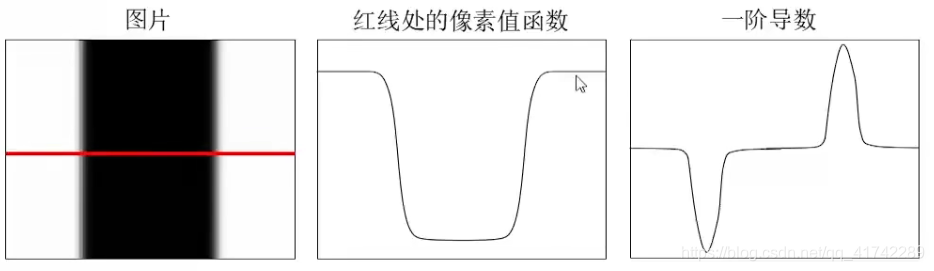
如下图,若黑色设为0,白色为255,则图1的红线部分灰度变化可以由图2表示,对图2求导得到图3.
灰度变化明显的区域 = 一阶导数的极值 = 边缘区域
2.1.2 过程优化
降噪: 上图举的例子是一个很简单的黑白图像,但是实际中的图像除了edge会产生灰度变化,其他的地方也会,比如:颜色过度不均匀的部分 ,噪声点部分等等。这些地方也会产生灰度值变化,反应到其一阶导数上会出现许多个极值点。
如何改进:降噪用高斯,平滑也用高斯。先用高斯模糊对图像平滑去噪,随后再使用一阶导数求极值。
2.1.3 边缘方向与梯度
大部分的边缘不是横竖的,往往都是倾斜的。这时简单的一阶导数无法检测出该边缘,可以使用类似于 f(x,y) 的形式,每一个点的函数值包括了横竖两个方向,原先的求一阶导数改为求一阶偏导数,这个就叫梯度。
梯度:
梯度强度 =
梯度方向 =
2.2、Corner
2.2.1 Harris角点
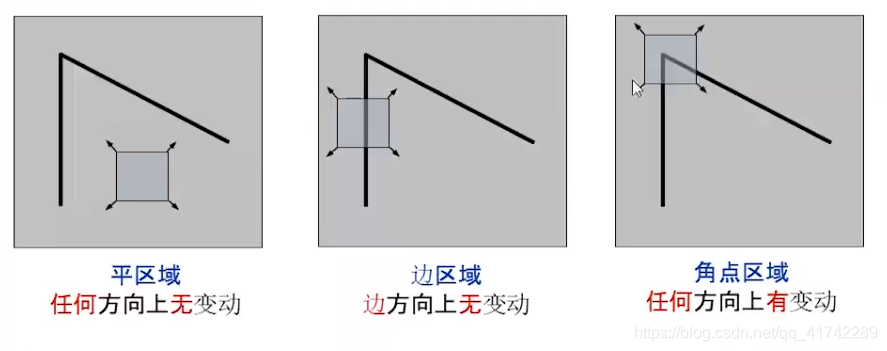
用一个小框在原图上移动,根据框中像素的变化,将原图分为几种区域
平区域: 框中像素在任何方向上都没有变化
边区域: 沿着边滑动时没有变化,垂直于边时有变化
角点区域: 滑动时任何方向都有变化
将框移动前后对应位置的像素强度作差,随后设定一个阈值,高于该阈值的就认为是一个Harris角点
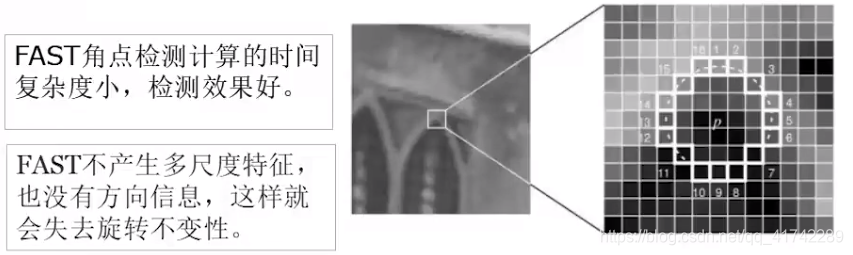
2.2.2 FAST 角点
简单描述:对于某个像素点,它与周围点看起来与众不同,那么它就是一个FAST角点。
具体过程:以某个待检测的点为圆心画一个半径为3的圆圈,如果圈内有超过n个点的像素值都比该点大,或者都比它小,那么就认为它是一个FAST角点。
2.3、Blob(斑点)
前面讲到过利用拉普拉斯梯度寻找边界的过程,即函数一阶导数的极值点为边缘部分。一阶导数的极值点,同样是二阶导数的零点。
斑点定义:二阶导数的极值点。因此,斑点应该是边缘中变化比较明显的部分。
与寻找边缘的过程一样,求二阶导数也很容易受到噪声的影响,因此需要先进行高斯降噪。
综上,先高斯降噪,再求拉普拉斯梯度寻找二阶导数极值点的过程,叫做高斯拉普拉斯滤波(LoG)。
补充: 拉普拉斯求导数对于边界很敏感,因此必须要先进行高斯模糊,把原图变模糊。高斯滤波的参数决定了模糊的程度,同时也决定了拉普拉斯二阶导数极大值,最终导致找出来的斑点数量的多少。
三、基于关键点的特征描述子
特征描述子:
对于同一个景物,从不同方向、天气等等去拍摄,拍出来的照片不同,但我们仍能够认出这是同一个景物。我们认为,这些不同的照片中,存在某些关键的特征描述点,使得能够分辨出这是同一个景物。
特征描述子应满足以下条件:
可重复、显著、抗图片变化(光照、亮度、平移)
3.1、SIFT
基于尺度空间不变的特征
3.1.1 什么是差分?
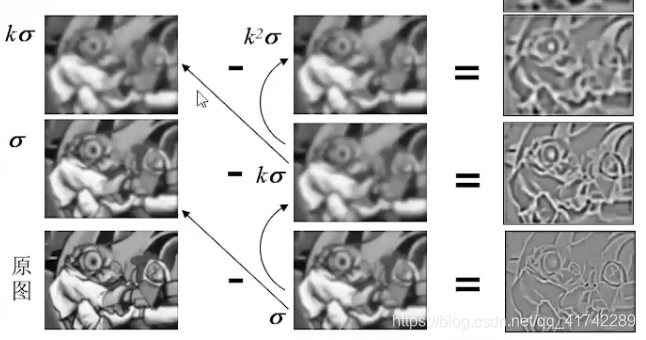
我们使用高斯拉普拉斯滤波(LoG)的目的是找边缘、斑点。而DoG的过程是这样的:
1、先对原图进行两次高斯滤波,一次 σ 大,一次 σ 小。得到的两个结果图应该是一个比较清晰一个比较模糊。
2、对两个图片做差,得到的图形就是边缘。
结论:LoG计算量很大,可以用DoG优化,即用差分代替微分。
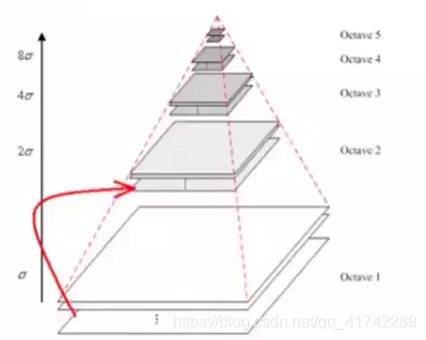
3.1.2 高斯金字塔
在传统金字塔的基础上,对每一层的图像进行不同程度σ的高斯滤波,得到的图形并为一组(octave)。
层与层之间:高斯降采样
每一层组中,图与图之间:不同程度σ的高斯滤波
随后,每一组中的不同图片,他们的尺寸大小相同,只是高斯滤波的σ不同,正好符合DoG的过程,因此直接对他们做差,得到的就是差分。可以想象,每一组得到的DoG图片中,都是相同的边缘,但边缘的模糊程度不同。
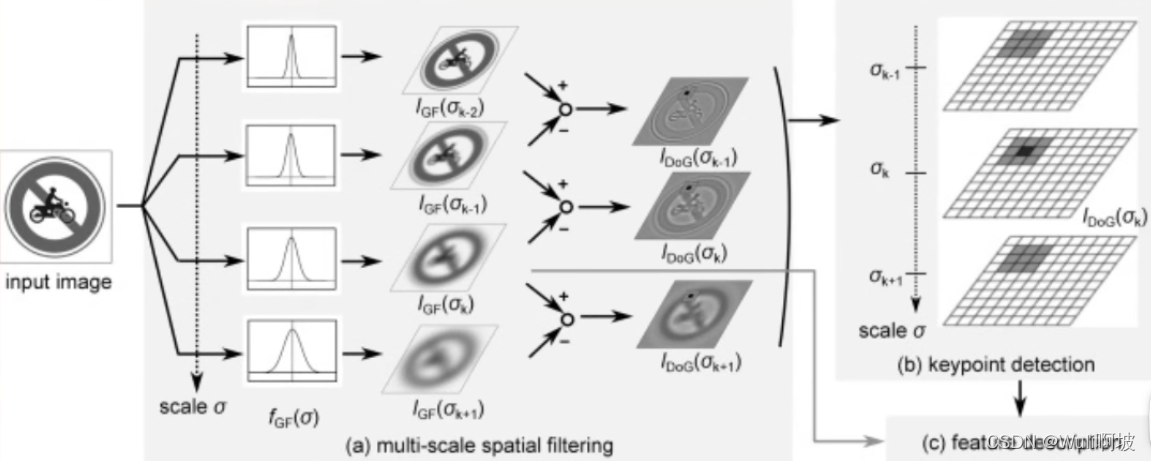
3.1.3 步骤一:尺度空间极值检测
以这张图为例,
1、对左侧的摩托车禁行标志图片进行高斯模糊,分四个不同的σ参数,得到四张不同参数的高斯模糊图片;
2、对四张图片进行差分操作,得到三幅差分图像;
3、遍历中间那副差分图片的所有点,如果某个点在相邻的上下双层共27个点之间,差分值最大或者最小,就认为这个点是特征点。
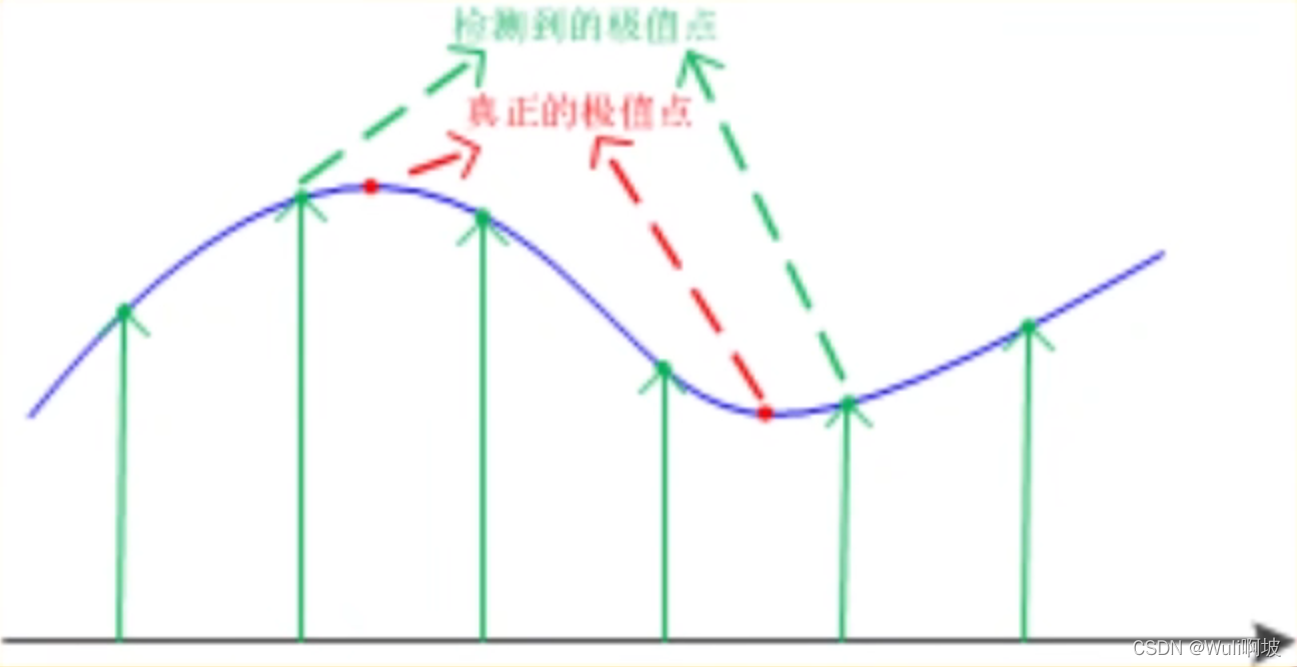
3.1.4 步骤二:关键点定位
由于高斯模糊的作用,步骤一中得到的特征点是离散的,不一定是真正的极值点位置,因此还需要类似于曲线拟合的方式来找到真正的极值点,至于怎么拟合,我不知道。
3.1.4 步骤三:方向赋值
找到特征点后,还需要确定该特征点的方向。
1、以某一特征点为中心,取31.5σ大小作为半径做圆,计算出该圆圈内所有像素的梯度方向和梯度幅值,图中只展示了八个方向,在原文中是以10°为一个方向,共36个方向。可见这方向也是离散的,需要通过拟合来得到真实的方向。
2、统计圈内所有点的梯度方向和梯度幅值,找出最大值,并以该方向作为这个特征点的主方向
3、重复操作,得到所有特征点的主方向
3.1.4 步骤四:关键点描述
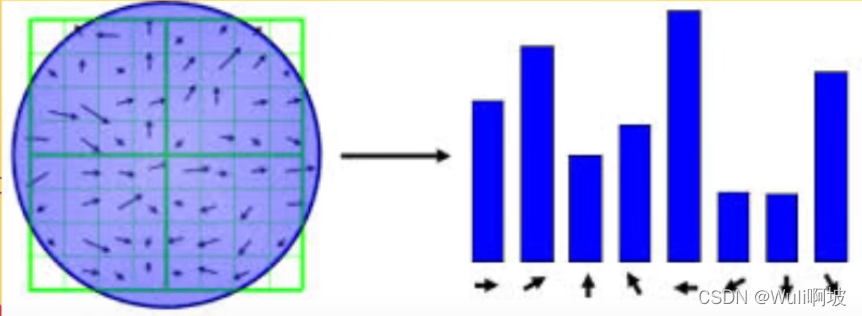
就是用关键点周围点的梯度幅值信息来描述这个点,过程如下
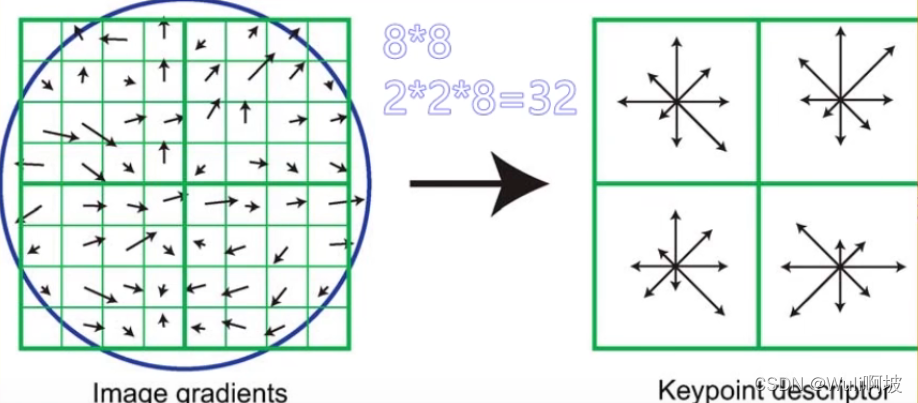
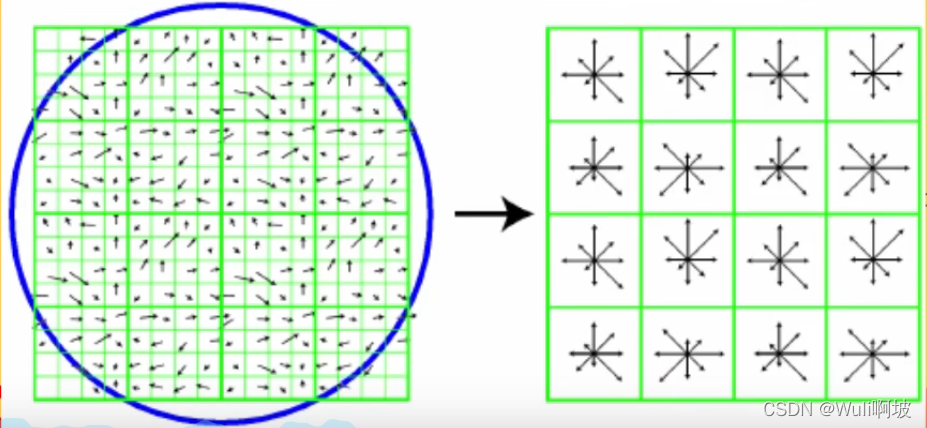
1、画一个 8 * 8 的圆,再把这个圆分成 4 * 4 的样子,一共是 4 份,如左图;
2、对每一份里的像素点,计算这个点的梯度幅值信息,统计得到直方图,如右图;
3、用这 4 个直方图来描述这个特征点,上图的方向只取 8 个角度。可见上图中的直方图一共是228个维度,即用这 32 个特征的描述器来描述这个特征点。
但是在SIFT原文中,用的是 16 * 16 的圆,最终构造的描述器就具有 4 * 4 * 8 = 128个特征。
3.2 SIFT 实例:图像拼接
以下作废
3.2、SURF
SURF是对SIFT的优化,可以把速度提升3倍
3.2.1、Haar-like特征
下面四个被称为特征模板,用于检测某些固定的特征。
比如A图,专门用于检测竖直的边界;B图专门检测水平的边界。在计算的时候,把模板套在原始图片上,用白色部分覆盖的像素值减去黑色部分覆盖的像素值。
这种计算过程产生的计算量非常大,可以采用积分图计算进行优化(这个不懂)
3.2.2、如何简化
算了,完全看不懂了,反正就是相比 SIFT 优化了