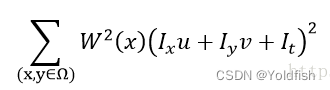前言

在使用PX4FLOW时，发现在蒙住声纳传感器时，相机仍然能够输出角速度，这让我感到很困惑，于是干脆学习一下光流算法，也为之后SLAM学习做一点铺垫。这篇总结主要参考这位博主的博文：T-Jhon

光流传感器基本测量思路

一个简单的光流传感器其实就是一个灰度图相机，它根据捕捉空间点在像素平面上的运动速度，推算出自身的速度。例如人坐在车上看窗外的马路向后运动（视网膜就是像素平面，马路向后运动就是空间点映射在像素平面的像素在视网膜上的运动），可以感知自己相对地面在向前运动。光流测量原理与之类似。

基本假设

按照上述的测量原理，我们默认了一个假设条件，那就是空间特定点在像素平面映射出来的那个像素点，无论什么时候，在像素的平面的哪个位置，它的光强都是不变的（灰度图的光强数值范围可以表示为[0,255]），依据这个条件，我们就能够估算出自身相对于空间点的运动。空间上一个特定点的光强用数学模型可以表示为：

$I(x,y,t)$
其中$I$表示光强，$x,y$表示空间特定点在像素平面的坐标，$t$表示拍摄这张图片时的时间戳

根据光强不变的假设我们可以得到下面等式：
$I(x,y,t)=I(x+dx,y+dy,t+dt)$

令$X=x+dx,Y=y+dy,T=t+dt$,则对$I(X,Y,Z)$在$(x,y,t)$处泰勒展开有：

$I(X,Y,Z)=I(x,y,t)+I_x（X-x）+I_y（Y-y）+I_t(T-t)+o$
其中$I_x,I_y,I_t$分别为$I$对$(X,Y,T)$的偏导

将$X=x+dx,Y=y+dy,T=t+dt$带入式子右边，舍弃高阶无穷小，有：
$I(X,Y,Z)-I(x,y,t)=I_{x}dx+I_{y}dy+I_{t}dt$

因为光强不变，所以$I(X,Y,Z)-I(x,y,t)=0$,所以：
$I_{x}dx+I_{y}dy+I_{t}dt=0$

式子左右同除$dt$，有：
$I_{x}dx/dt+I_{y}dy/dt+I_t=0$

令$dx/dt=u,dy/dt=v$（也就是像素点的速度），上述式子可表示为：
$I_{x}u+I_{y}v+I_t=0$

现在，$I_x，I_y，I_t$已知，一个方程两个未知数，方程不可解，还需要引入其他约束；

根据引入其他约束的方式不同，光流法可分为：基于梯度（微分）的方法、基于匹配的方法、基于能量（频率）的方法、基于相位的方法和神经动力学方法。详细请见T-Jhon

LK法

LK法引入了一个新的假设条件：一个像素点的小领域内所有的像素点的运动方向与中心点相同，也就是它们有相同的$u，v$，这样一来就可以引入多个方程来估计$u，v$的值了。

采用的估计方法为最小二乘法，表示如下：

其中，$W$是一个窗口权重函数，该函数使得邻域中心的加权比周围的大.

类似这篇博文，将其转为向量表达式，假设领域内共有n个像素点：
首先转换$W$：可以看出$W$需要转换为一个对角矩阵，为了下面书写方便，该对角阵仍记为$W$，维度为$(n,n)$.
转换$I_{x}u+I_{y}v$：设$I=[I_x,I_y]，S=[u,v{]}^T$，则$I_{x}u+I_{y}v=IS$，其中$I$的维度为$(n,2)$，S的维度为(2,1)(这里不是n，是因为假设的领域内有相同的u，v)
转换$I_t$：时间向量记为$T$.
则原求和表达式可写为：
$[W(IS+T){]}^T[W(IS+T)]$
先乘开，然后对S求导，令导数为零得：
$S=-(I^T{W}^{2}I{)}^{-}(I^T{W}^{2}T)$
详细推导可参看这篇博文
S即为[u,v]，便得到了像素点的速度。

疑问

目前也只是在求像素点的速度，按理要转换为角速度的话，是需要一个距离信息的，但是遮住PX4FLOW声纳传感器时，光流依旧能够正常输出角速度值，这是怎么做到的？