给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

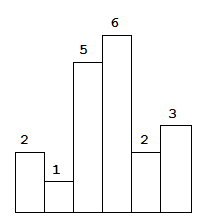
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

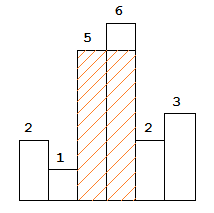
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

法一：暴力

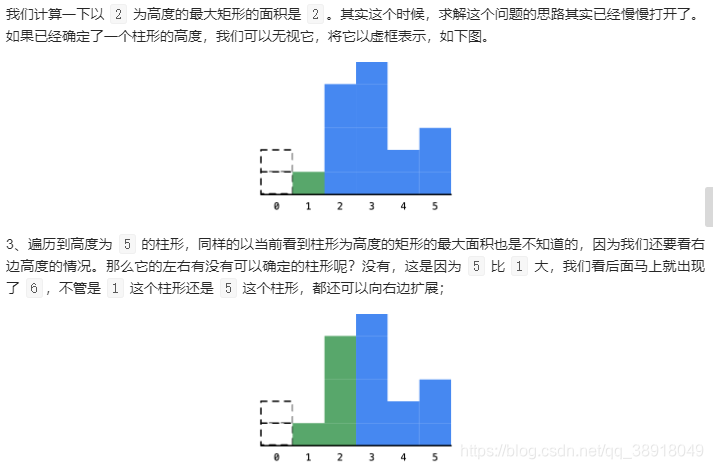
左边看一下，看最多能向左延伸多长，找到大于等于当前柱形高度的最左边元素的下标；

右边看一下，看最多能向右延伸多长；找到大于等于当前柱形高度的最右边元素的下标。

对于每一个位置，我们都这样操作，得到一个矩形面积，求出它们的最大值。

public class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        if (len == 0) return 0;

        int res = 0;
        for (int i = 0; i < len; i++) {

            int left = i;
            int curHeight = heights[i];
            while (left > 0 && heights[left - 1] >= curHeight) {
                left--;
            }

            int right = i;
            while (right < len - 1 && heights[right + 1] >= curHeight) {
                right++;
            }

            int width = right - left + 1;
            res = Math.max(res, width * curHeight);
        }
        return res;
    }
}

法二：栈

public class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        Stack<Integer> s = new Stack<>();
        int maxArea = 0;
        for (int i = 0; i <= len; i++){
            int h = (i == len ? 0 : heights[i]);
            if (s.isEmpty() || h >= heights[s.peek()]) {
                s.push(i);
            } else {
                int tp = s.pop();
                maxArea = Math.max(maxArea, heights[tp] * (s.isEmpty() ? i : i - 1 - s.peek()));
                i--;
            }
        }
        return maxArea;
    }
}

就这样一直消