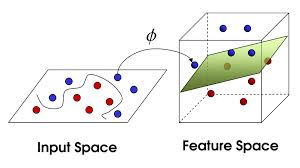
机器学习算法中,不论是感知机还是支持向量机,在面对非线性问题时,往往都会用到一个名为“核函数”的技巧。那么到底什么是核函数呢?是否真的如听起来这样难以理解呢?
核函数:是映射关系
二维映射到三维,区分就更容易了,这是聚类、分类常用核函数的原因。为什么PCA这样一个降维算法也用核函数呢?
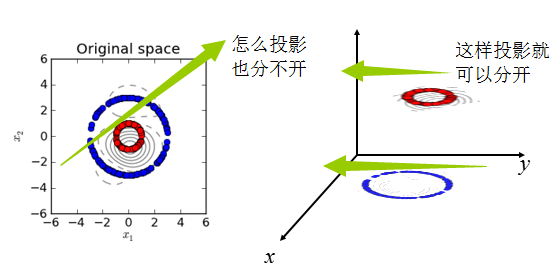
左图为原数据,右图为映射到三维的数据,可以看出:同样是降到1维,先通过Kernel映射到(Kernel是映射的内积,不要弄乱了)三维,再投影到1维,就容易分离开,这就是Kernel在PCA降维中的应用,本质还是对原有数据增加维度。
下面是李航的《统计学习方法》中对于核函数的定义:
要注意,核函数和映射没有关系。核函数只是用来计算映射到高维空间之后的内积的一种简便方法。
一般英文文献对Kernel有两种提法,一是Kernel Function,二是Kernel Trick。从Trick一词中就可以看出,这只是一种运算技巧而已,不涉及什么高深莫测的东西。
具体巧在哪里呢?我们如果想进行原本就线性不可分的数据集进行分割,那么选项一是容忍错误分类,即引入Soft Margin;选项二是我们可以对Input Space做Feature Expansion,把数据集映射到高维中去,形成了Feature Space。我们几乎可以认为(引用Caltech的课堂用语“We are safe but not certain”)原本在低维中线性不可分的数据集在足够高的维度中存在线性可分的超平面。
举一个知乎上霍华德的例子。假设我们的任务是要预测那些微博可以上微博热搜榜。有两个离散特征,一个代表某个微博里有“鹿晗”,一个代表某个微博里有“关晓彤”。
两个特征单独看热度都一般,此时我们用二阶多项式核方法:
这个核函数可以把二维空间投射到三维空间,展开之后是:

这样就把二维特征变成了三维,多了一维 
结果大家都知道了,鹿晗关晓彤同时出现的那条微博超级火,把新浪服务器都挤爆了。
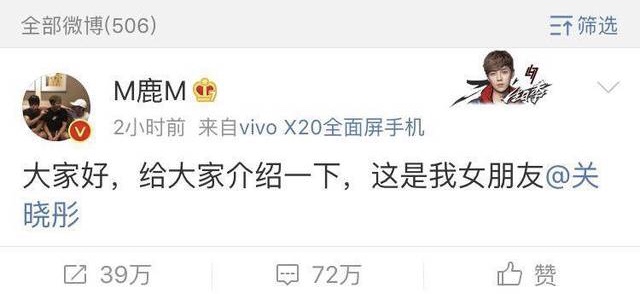


现实生活中有很多非线性非常强的特征 而核方法能够捕捉它们。核技巧(kernel trick)的作用,一句话概括的话,就是降低计算的复杂度,甚至把不可能的计算变为可能。
在机器学习中常用的核函数,一般有这么几类,也就是LibSVM中自带的这几类:
1) 线性:
2) 多项式:
3) Radial basis function:
4) Sigmoid:
我举的例子是多项式核函数中
在实用中,很多使用者都是盲目地试验各种核函数,并扫描其中的参数,选择效果最好的。至于什么样的核函数适用于什么样的问题,大多数人都不懂。很不幸,我也属于这大多数人,所以如果有人对这个问题有理论性的理解,还请指教。
参考文章: