1，什么是数据结构？

“数据结构（Data Structure）是数据对象、存在于该对象的实例以及组成实例的的数据元素之间的各种关系，并且这种关系可以通过定义相关的函数来给出。”-via《数据结构、算法于应用》。简单理解就是可以结构化表示的数据间关系。

“数据结构是抽象数据类型ADT的物理实现。”-via《数据结构与算法分析》。可见结构化数据的过程就是数据结构实现的过程。

我们再来分析一下里面的几个概念：

数据：数据是信息的载体，它应该能够被计算机识别、加工和存储。日常所见，数字、字符、图像、视频、声音等皆为数据。数据元素：数据元素是数据的基本单位。数据项：数据项就是数据元素中的字段、属性等。比如，我们把一张数据库表看作是一份数据，那么数据元素就是里面的每条记录，数据项就是每个字段。

所以简而言之，数据结构就是表示数据间关系的集合。

2，什么是算法？

算法(Algorithm)是用来操作程序，解决问题的一组方法，它通常可以用来解决一类问题。它需满足五个特性：

输入：零个或多个输入。

输出：一个或多个输出。

有穷性：有限步骤后在可接受时间内完成。

确定性：每个步骤都有确定含义，无二义性。

可行性：每一步都是可行的。

3，复杂度分析

我们通常用时间复杂度和空间复杂度来衡量算法的优劣。

• 时间复杂度：用于评估执行程序所消耗的时间，可以估算出程序对处理器的使用程度；
• 空间复杂度：用于评估执行程序所占用的内存空间，可以估算出程序对计算机内存的使用程度。

通常我们主要分析的是程序的时间复杂度。而时间复杂度又有最好、最坏、平均之说。我们一般关注的是最坏的情况。

时间复杂度分析：大O表示法$$O(1)常数阶<O(lo{g}_n)对数阶<O(n)线性阶<O(nlo{g}_n)线性对数阶<O(n^2)平方阶<O(2^n)指数阶$$

由下图可知随着数量的不断提升，复杂度的变化越来越大。

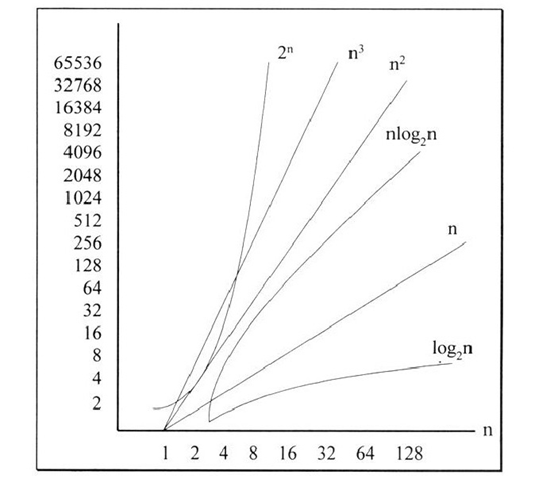
tips:分析时间复杂度，我们只需要找程序的最小执行语句，分析他的执行次数，通常聚焦于循环体内；时间复杂度表示，我们一般取阶数最高的做为最终的复杂度，所有常数阶均取作1，均不带系数。

分析实例：

//T(n)=O(1)
int i=1;
int s = i+1; 

即使变量有很多个，每个语句的执行次数也是1，我们关注的是最小执行单元。

//T(n)=O(logn),log2n一般以logn表示
int i =1;
while(i < n){
    i = i * 2; //此时1*2*2*2*...=n;即log2n个2相乘
}

//T(n)=O(n)
int s = 0;
for(i = 1;i <n;i++){
	s += i;
}

//T(n)=O(nlogn)
for(int i = 1;i < n;i++){
	int j = 0;
	while(j<n){
		j = j * 2;
	}
}

内层判断执行 logn 次，外面循环执行 n 次；即 nlogn

//T(n)=O(n^2)
int k = 0;
for(int i = 0;i < n;i++){
	for(int j = 0;j < n;j++){
		k = i+j;
	}
}

数据结构是一个程序的灵魂，大型复杂的系统之中必然涉及到数据结构和算法的使用。
通常，程序=数据结构+算法。

数据结构的逻辑结构分类：

• 线性结构
• 非线性结构

其中线性结构又可以分为顺序存储结构和链式存储结构：包括数组、队列、链表、栈;
非线性结构：多维数组、广义表、树结构、图结构。