Bootstrap

红黑树删除节点——这一篇就够了

红黑树

红黑树常用的操作是插入、删除和查找，并且它对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保，对于红黑树的概念、性质、插入、查找和旋转等这里不再多讲，不了解的请点击wikipedia rb-tree，这里重点讲一下红黑树的删除，这是红黑树中最难但又必须使用的操作。

红黑树的5条性质:

  1. 节点是红色或黑色。
  2. 根是黑色。
  3. 所有叶子都是黑色（叶子是NIL节点）。
  4. 每个红色节点的父子节点都不能为红色。
  5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
      

可能出现的组合

红黑树的删除之所以难就是因为删除节点遇到的情形太多，容易把人绕晕，那么接下来这篇将一步一步的分析各种情形，只要你静下心来慢慢的分析，将各种情况分清楚，那么写代码就显得比较简单了。

红黑树中删除一个节点，遇到的各种情形就是其子节点的状态和颜色的组合，子节点状态共有3种：无子节点、有一个子节点、有两个子节点，颜色有红色和黑色两种，所以共会有6种组合。接下来我们逐一分析：
  

组合1：被删节点无子节点，且被删结点为红色

这是最简单的一种情况，直接将节点删除即可，不破坏任何红黑树的性质
  

组合2：被删结点无子结点，且被删结点为黑色

这是最复杂的情况，我们稍后再讨论
  

组合3：被删结点有一个子结点，且被删结点为红色

在这里插入图片描述
这是一种不可能的情况，此时不符合性质5
  

组合4：被删结点有一个子结点，且被删结点为黑色

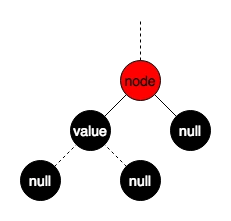
在这里插入图片描述
这种组合下，被删结点node的另一个子结点value必然为红色，此时直接将node删掉，用value代替node的位置，并将value着黑即可。
  

组合5&6：被删结点有两个子结点，且被删结点为黑色或红色

当被删结点node有两个子结点时，我们先找到这个被删结点的后继结点successor（前驱节点也可以），然后用successor替换node的值，不用改变颜色，此时转换为删除node的后继节点successor。

这里使用node的后继节点替换node，必然是下图两种形态中的一种:
在这里插入图片描述
若是(a)的情形，用successor代替node后，转换为successor被删，若successor为红色，则变成了组合1；若successor为黑色，则变成了组合2。

若是(b)的情形，用successor代替node后，转换为successor被删，若successor为红色，则变成了组合1（组合3是不可能的）；若successor为黑色，则变成了组合2或4。
  
  
综上所述：组合5 6被转换为前面几种组合，我们真正要进行删除的只有组合1 2 4，对于组合1和4，删除操作相当简单，这里不再多讲，接下来再逐一分析组合2可能的几种情形。
  
  
  

再论组合2：被删结点无子结点，且被删结点为黑色

因为删除黑色结点会破坏红黑树的性质5，所以为了不破坏性质5，将node删除后用一个拥有额外黑色的null替代它（可以想象是将node删除后，在这个位置放了一个黑色的权值），剩下的就是调平的过程，最终这个游离的黑色权值被扔掉，整个删除操作完成。
在这里插入图片描述
然后再结合node的父结点father和其兄弟结点brother来分析。
  
  

情形一：brother为黑色，且brother有一个与其方向一致的红色子结点son

所谓方向一致，是指brother为father的左子结点，son也为brother的左子结点；或者brother为father的右子结点，son也为brother的右子结点。
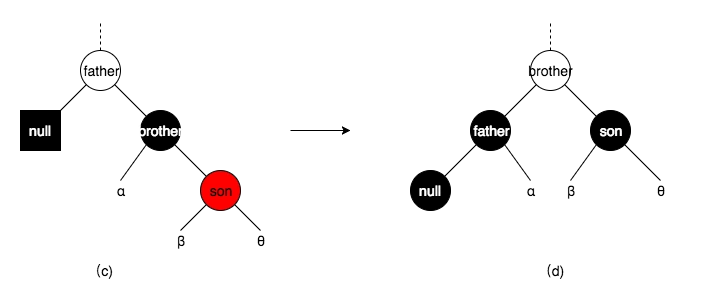
在这里插入图片描述
图(c )中，白色代表随便是黑或是红，方形结点存储的是一个游离的黑色权值。将brother和father旋转（是左旋还是右旋自己根据情景体会，下同），并重新上色后，变成了图(d)，将游离的黑色权值扔掉，此时不违背任何红黑树的性质，删除操作完成。

图(c )中的情形颠倒过来，也是一样的操作。
  
  

情形二：brother为黑色，且brother有一个与其方向不一致的红色子结点son

在这里插入图片描述
图(e)中，将son和brother旋转，重新上色后，变成了图(f)，转化为情形一。

图(e)中的情形颠倒过来，也是一样的操作。
  
  

情形三：brother为黑色，且brother无红色子结点

此时若father为红，则重新着色即可，删除操作完成。如图下图(g)和(h)
在这里插入图片描述
此时若father为黑，则重新着色，将游离的黑色权值存到father（此时father的黑色权重为2），将father作为新的结点进行情形判断，遇到情形一、情形二，则进行相应的调整，完成删除操作；如果没有，则结点一直上溯，直到根结点存储额外的黑色，此时将该额外的黑色扔掉，即完成了删除操作。
在这里插入图片描述
注意： 这里第二种情况有点不好理解，之所以要加一个游离的黑色是因为删除node后造成node子树和brother子树的黑节点个数不平衡，这里的操作实际是将brother子树中黑节点个数减少一个，而将father黑色权重设为2，这样father左右两边的子树不用加游离的权值都是平衡的了。接下来将问题转移到了father、father的father、father的brother三个之间，这样向上递归，如果一直是这种情况，最终必定转化为root的左子节点或者右子节点权重为2，同样的将root黑色权重设为2，将另外一边的黑色权重减小1，再将root的黑色权重扔掉一个，此时整棵树重回平衡，只是root到叶节点路径的黑节点少了一个。
  
  

情形四：brother为红色，则father必为黑色。

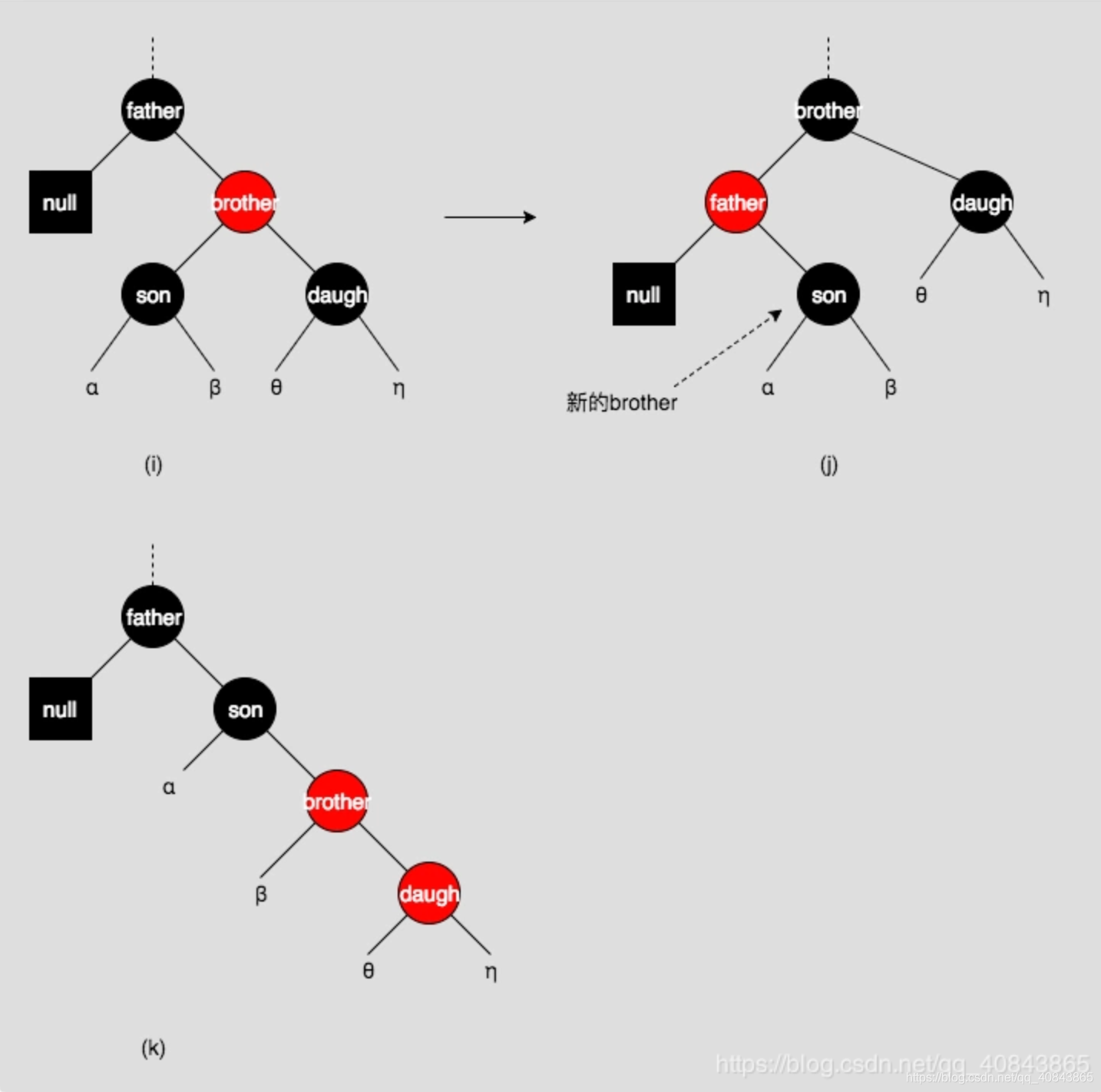
在这里插入图片描述
图(i)中，将brother和father旋转，重新上色后，变成了图(j)，新的brother（原来的son）变成了黑色，这样就成了情形一、二、三中的一种。如果将son和brother旋转，无论怎么重新上色，都会破坏红黑树的性质4或5，例如图(k)。
图(i)中的情形颠倒过来，也是一样的操作。
  
至此，所有情形都以分析完毕，总的来说，我们要处理的是3种组合、7种情形，其中很多过程都是目标转移的过程，最终转移到可以通过旋转和变色达到平衡的节点或者转移到root节点，使红黑树重回平衡。
  
  
  
以下是实现了红黑树的删除操作，对于红黑树的完整实现请点这里
  
  

代码实现：

//以下root_ptr为指向root节点的指针，leftmost_ptr为指向最左节点的指针，rightmost_ptr为指向最右节点的指针

node_pointer& root() {
	return root_ptr;
}

node_pointer& leftmost() {
	return leftmost_ptr;
}

node_pointer& rightmost() {
	return rightmost_ptr;
}

/* 删除节点 x，并进行相应的调整 */
void __erase_node(node_pointer x)
{
	if (x->left == nullptr && x->right == nullptr)	//删除叶节点
	{
		if (x->color == __rb_tree_red)		//组合1：删除红色的叶节点，直接删除即可（因为红节点不可能是root）
		{
			if (leftmost() == x)
				leftmost() = (node_pointer)x->parent;
			else if (rightmost() == x)
				rightmost() = (node_pointer)x->parent;
		}
		else {									//组合2：最麻烦的情况
			if (root() == x) {	//删除根节点
				root() = nullptr;
				leftmost() = header;
				rightmost() = header;
			}
			else {		//否则调用组合2的处理函数，此时x一定有兄弟节点（你不妨画个图出来看一下）
				__erase_node_case2_reblance(x);

				if (leftmost() == x)
					leftmost() = (node_pointer)x->parent;
				if (rightmost() == x)
					rightmost() = (node_pointer)x->parent;
			}
		}

		if (x->parent->left == x)
			x->parent->left = nullptr;
		else
			x->parent->right = nullptr;

		destroy_node(x);
		--node_count;
	}
	else if (x->left == nullptr) {		//一定是组合4：x是黑节点，它的右孩子是红节点（因为组合3不可能存在）
		node_pointer son = (node_pointer)x->right;
		son->parent = x->parent;
		son->color = __rb_tree_black;

		if (x->parent->left == x)
			x->parent->left = son;
		else
			x->parent->right = son;

		if (root() == x) {		//如果删除的是root节点，一点要调整相关指针
			root() = son;
		}
		if (leftmost() == x)
			leftmost() = son;

		destroy_node(x);
		--node_count;
	}
	else if (x->right == nullptr) {		//一定是组合4：x是黑节点，它的左孩子是红节点（因为组合3不可能存在）
		node_pointer son = (node_pointer)x->left;
		son->parent = x->parent;
		son->color = __rb_tree_black;

		if (x->parent->left == x)
			x->parent->left = son;
		else
			x->parent->right = son;
		
		if (root() == x) {		//如果删除的是root节点，一点要调整相关指针
			root() = son;
		}
		if (rightmost() == x)
			rightmost() = son;

		destroy_node(x);
		--node_count;
	}
	else {								//组合5、6：x有两个儿子
		iterator it = iterator(x);
		++it;	//这里找x的后继，也可以找x的前驱
		x->value_field = *it;

		__erase_node((node_pointer)it.node);	//转化为删除节点x的前驱，会回到组合1 2 4中的一种
	}
}

/* 组合2处理函数（这里只是进行旋转或者变色，并不删除节点） */
// 这里传入的x在算法思路上我们认为它含有一个额外的黑色权重，且x一定有brother节点
void __erase_node_case2_reblance(node_pointer x) {
	node_pointer brother = (node_pointer)x->get_brother();

	if (brother->color == __rb_tree_black)		//情形一 二 三
	{
		if ((brother->left && brother->left->color == __rb_tree_red) ||		//情形一 二
			(brother->right && brother->right->color == __rb_tree_red))
		{
			if (brother == x->parent->right)
			{
				if (brother->right != nullptr) {	//情形一
					__rb_tree_rotate_left(x->parent, header->parent);
					brother->right->color = __rb_tree_black;
					brother->color = x->parent->color;
					x->parent->color = __rb_tree_black;
				}
				else {							//情形二
					__rb_tree_rotate_right(brother, header->parent);
					brother->color = __rb_tree_red;
					brother->parent->color = __rb_tree_black;  //这里brother->parent是原来brother的儿子节点

					__erase_node_case2_reblance(x);	  //这里回到情形一，递归重新调整
				}
			}
			else	//brother == x->parent->left
			{
				if (brother->left != nullptr) {	  //情形一
					__rb_tree_rotate_right(x->parent, header->parent);
					brother->left->color = __rb_tree_black;
					brother->color = x->parent->color;
					x->parent->color = __rb_tree_black;
				}
				else {							//情形二
					__rb_tree_rotate_left(brother, header->parent);
					brother->color = __rb_tree_red;
					brother->parent->color = __rb_tree_black;  //这里brother->parent是原来brother的儿子节点

					__erase_node_case2_reblance(x);	//这里回到情形一，递归重新调整
				}
			}
		}
		else					//情形三
		{
			if (x == root())	//递归结束
				return;
			if (x->parent->color == __rb_tree_red)	//情形3.1
			{
				x->parent->color = __rb_tree_black;
				brother->color = __rb_tree_red;
			}
			else {				//情形3.2
				brother->color = __rb_tree_red;

				__erase_node_case2_reblance((node_pointer)x->parent);	//对parent递归这个过程（这时parent在算法思想上黑色权重为2）
				//以上将brother子树的黑节点减少一层，将x的黑色权重2（只是在算法思路上存在）移一个到father，
				//递归这个过程，直至遇到其他情形解决问题或递归到根节点
			}
		}
	}
	else				//情形四（brother为红，x->parent一定为黑）
	{
		if (brother == x->parent->right) {
			__rb_tree_rotate_left(x->parent, header->parent);
		}
		else {
			__rb_tree_rotate_right(x->parent, header->parent);
		}

		brother->color = __rb_tree_black;
		x->parent->color = __rb_tree_red;

		__erase_node_case2_reblance(x);		//对x重新执行这个过程，此时一定是情形一 二 三中的一种
	}
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
蒙特卡洛树搜索的主要流程有哪些_蒙特卡洛树是什么算法？
面试技术栈 —— 2024网易雷火暑期实习真题
计算机硬盘哒哒响,教你轻松解决硬盘异响(咔咔或者嗒嗒声)
Ubuntu下通过docker安装wechat
创建、修改Docker容器网络地址
springboot“小鱼在乎”日程计划系统-计算机毕业设计源码51307
Stable Diffusion教程 | Controlnetv1.1之Openpose
ValueError: need more than 2 values to unpack
vue js中对包含字典的数组根据某属性进行排序
【经验分享】将ui文件转化成py代码
;