关系模型
关系数据库的结构
属性
- 每个属性允许的值的集合称为属性的域
- 属性值(通常)需要是原子的;也就是说,不可分割
- 特殊值null是每个域的成员。表示该值为“未知”
- 空值在许多操作的定义中造成了复杂性
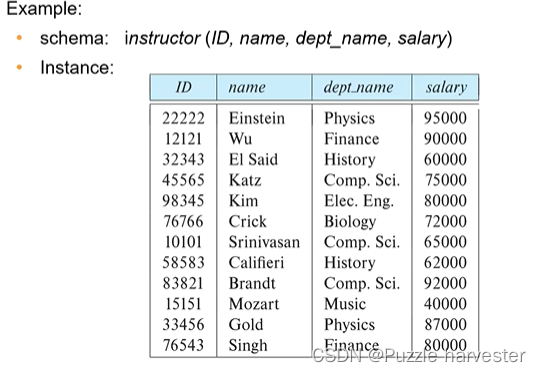
数据库模式
数据库模式(schema)——是数据库的逻辑结构
数据库实例(instance)——是数据库中数据在给定时刻的快照
键
- 让 k ⊆ R k \subseteq R k⊆R
- 如果K的值足以识别每个可能关系r®的唯一元组,则K是R的超码(super key)
- 如果K是最小值,则是一个候选码(candidate key)
- 选择一个候选键作为主键(primary key)
- 外键约束(Foreign key):一个关系中的值必须出现在另一个关系中
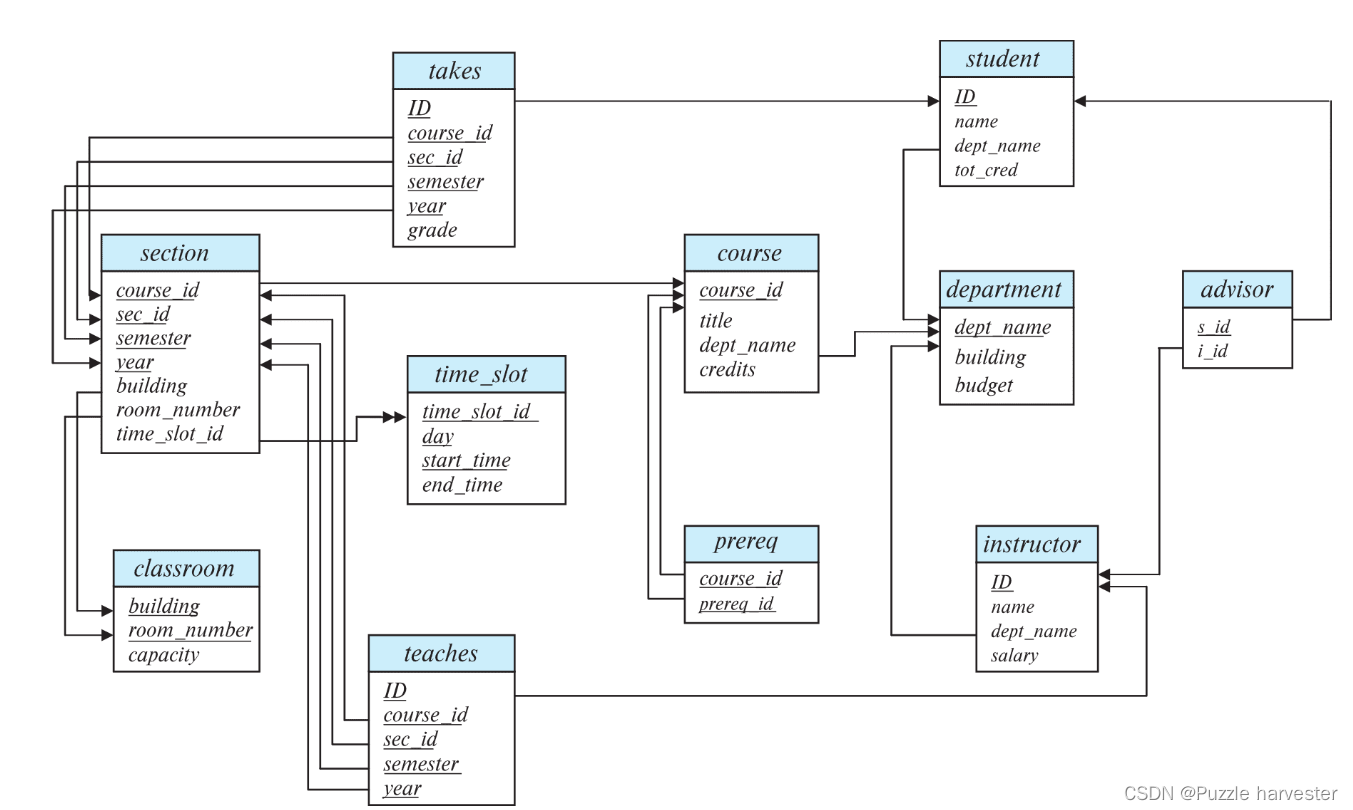
架构图
关系查询语言
- 程序性与非程序性或说明性的对比
- “纯”语言:
- 关系代数
- 元组关系演算
- 域关系演算
- 以上3种纯语言在计算能力上是等价的
- 我们将在本章集中讨论关系代数
- 不是图灵机等效
- 包含6个基本操作
关系代数
一种过程语言,由一组以一个或两个关系作为输入并产生一个新关系作为其/结果的操作组成。
六种基本操作:
-
选择操作
- select操作选择满足给定谓词的元组
- 符号: σ p ( r ) \sigma_p(r) σp(r)
- p被称为选择谓词
-
投影操作
- 一个一元运算,它返回其参数关系,但省略了某些属性
- 符号:
Π
A
1
,
A
2
,
A
3
,
.
.
.
,
A
K
(
r
)
\Pi_{A_1,A_2,A_3,...,A_K}(r)
ΠA1,A2,A3,...,AK(r)
- 其中 A 1 , A 2 , . . . , A K A_1,A_2,...,A_K A1,A2,...,AK是属性名,r是关系名
- 结果被定义为通过擦除未列出的列得到的K列的关系
- 从结果中删除重复行,因为关系是集合的
- 关系操作的组成
- 关系代数运算的结果就是关系,因此关系代数运算可以组合成一个关系代数表达式
- 考虑以下查询—查找物理系所有教员的姓名
- Π n a m e ( σ d e p t _ n a m e = " P h y s i c s " ( i n s t r u c t o r ) ) \Pi_{name}(\sigma_{dept\_ name = "Physics"}(instructor)) Πname(σdept_name="Physics"(instructor))
- 我们没有将关系的名称作为投影操作的参数,而是给出一个求值为关系的表达式
-
笛卡儿积运算
- 笛卡尔积运算(用 × \times ×表示)允许我们结合来自任何两个关系的信息。
- 例子:讲师和教授的关系的笛卡尔积被写成: i n s t r u c t o r × t e a c h e s instructor \times teaches instructor×teaches
- 我们从每一对可能的元组中构造一个结果元组:一个来自讲师关系,一个来自讲师关系
- 由于教师ID出现在两个关系中,我们通过将属性最初来自的关系的名称附加到属性来区分这些属性
- i n s t r u c t o r . I D instructor.ID instructor.ID
- t e a c h e s . I D teaches.ID teaches.ID
-
连接操作
- 为了只获得那些“ i n s t r u c t o r × t e a c h e s instructor \times teaches instructor×teaches”的元组,这些元组与教师和他们教授的课程有关,我们写: σ i n s t r u c t o r . i d = t e a c h e s . i d ( i n s t r u c t o r × t e a c h e s ) \sigma_{instructor.id = teaches.id}(instructor \times teaches) σinstructor.id=teaches.id(instructor×teaches)
- 连接操作允许我们将选择操作和笛卡尔积操作组合为单个操作
- 考虑关系式r®和s(S)
- 设"theta"是模式R"union"s中属性的谓词。联接操作 r ⋈ θ r \Join_{\theta} r⋈θ定义如下: r ⋈ θ s = σ θ ( r × s ) r \Join_{\theta}s=\sigma_{\theta}(r \times s) r⋈θs=σθ(r×s)
- 因此 σ i n s t r u c t o r . i d = t e a c h e s . i d ( i n s t r u c t o r × t e a c h e s ) \sigma_{instructor.id = teaches.id}(instructor \times teaches) σinstructor.id=teaches.id(instructor×teaches)可以等价地写成 i n s t r u c t o r ⋈ i n s t r u c t o r . i d = t e a c h e s . i d t e a c h e s instructor \Join_{instructor.id=teaches.id}teaches instructor⋈instructor.id=teaches.idteaches
-
联合操作
- 联合操作允许我们合并两个关系
- 符号: r ∪ s r \cup s r∪s
- 关于
r
∪
s
r \cup s
r∪s的有效:
- r , s r,s r,s必须具有相同的属性(相同数量的属性)
- 属性域必须兼容(例如:r的第二列处理与s的第二列相同类型的值)
-
Set-Intersection操作
- 集合交集操作允许我们找到两个输入关系中的元组
- 符号: r ∩ s r \cap s r∩s
- 假设:
- r和s具有相同的性质
- r和s的属性兼容
-
集差操作
- 集差操作允许我们找到在一种关系中但不在另一种关系中的元组
- 符号: r − s r-s r−s
- 相容关系之间必须取集差
- r和s必须具有相同的性质
- r和s的属性域必须兼容
-
赋值操作
- 有时,通过将关系代数表达式的一部分分配给临时关系变量来编写关系代数表达式是很方便的
- 赋值操作用" ← \leftarrow ←"表示,工作方式类似于编程语言中的赋值
-
更名操作
- 关系代数表达式的结果没有我们可以用来引用它们的名称。更名操作符 ρ \rho ρ就是为此目的而提供的
- 表达式:
ρ
X
(
E
)
\rho_X(E)
ρX(E)
- 返回名称为x的表达式E的结果
-
等价操作
- 关系代数表达式的结果没有我们可以用来引用它们的名称。更名操作符 ρ \rho ρ就是为此目的而提供的
- 表达式:
ρ
X
(
E
)
\rho_X(E)
ρX(E)
- 返回名称为x的表达式E的结果
-
等价操作
- 在关系代数中,编写查询的方法不止一种