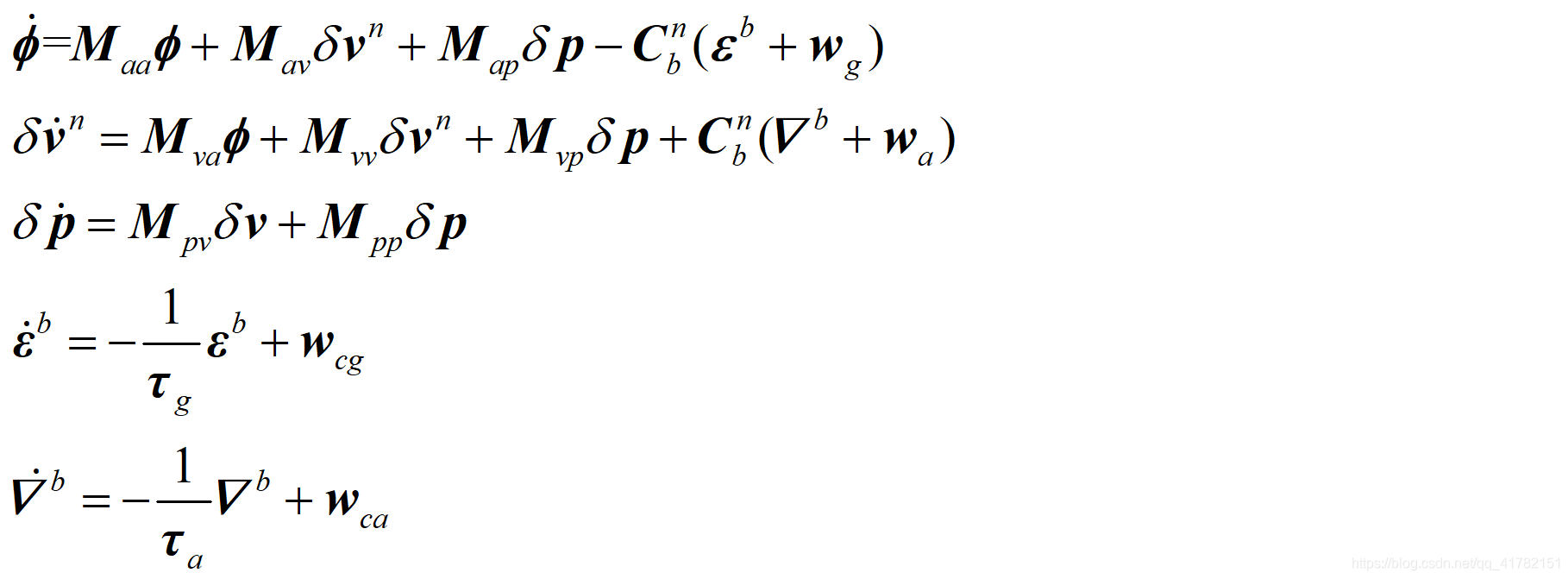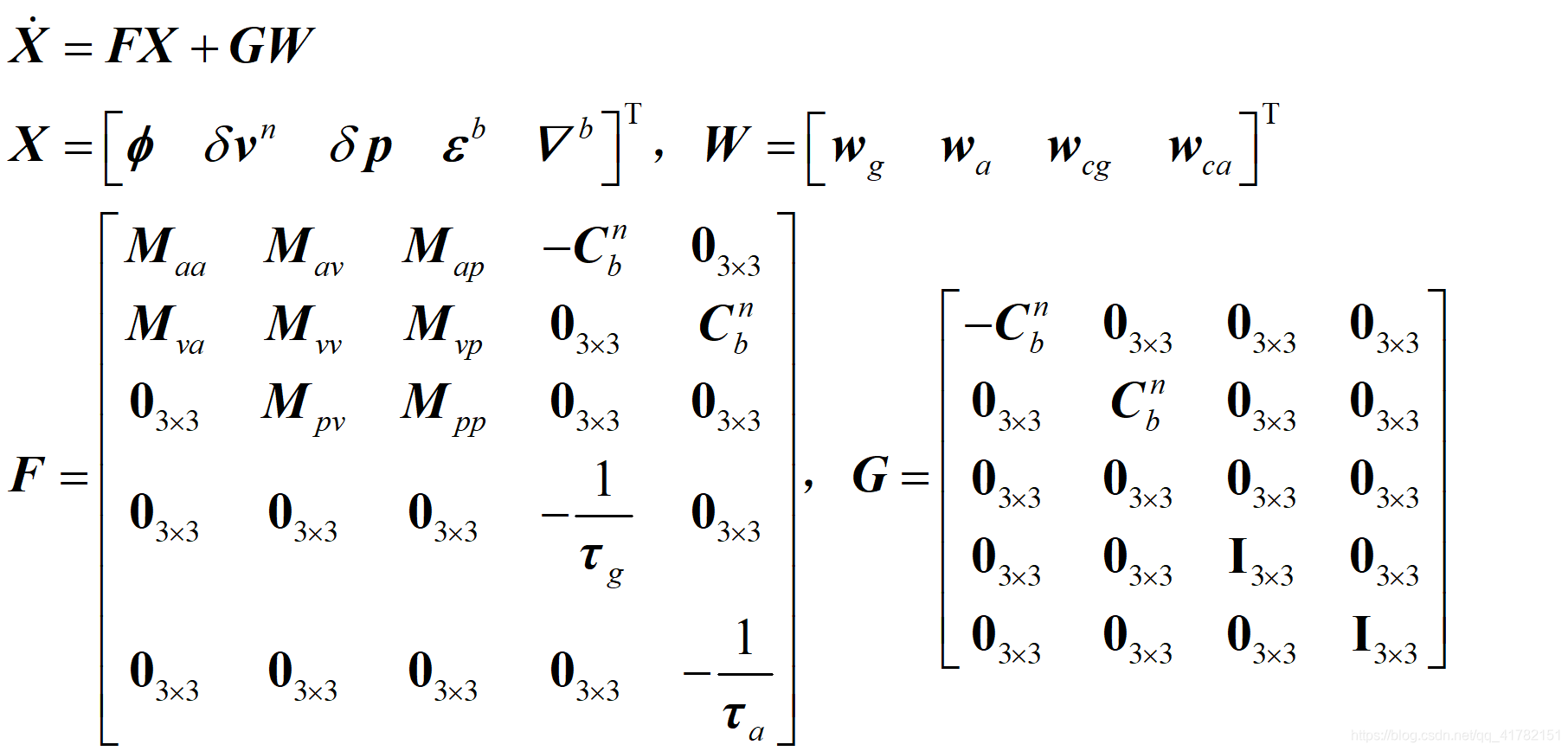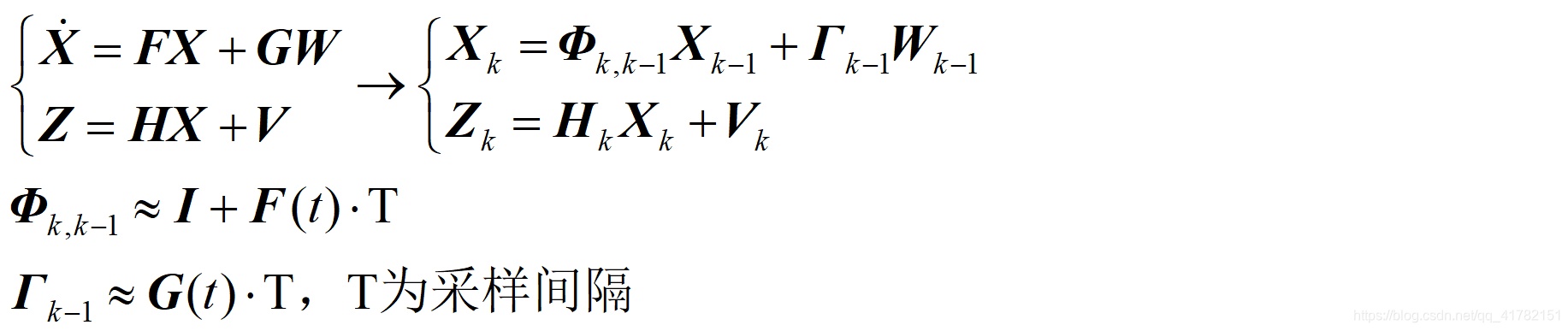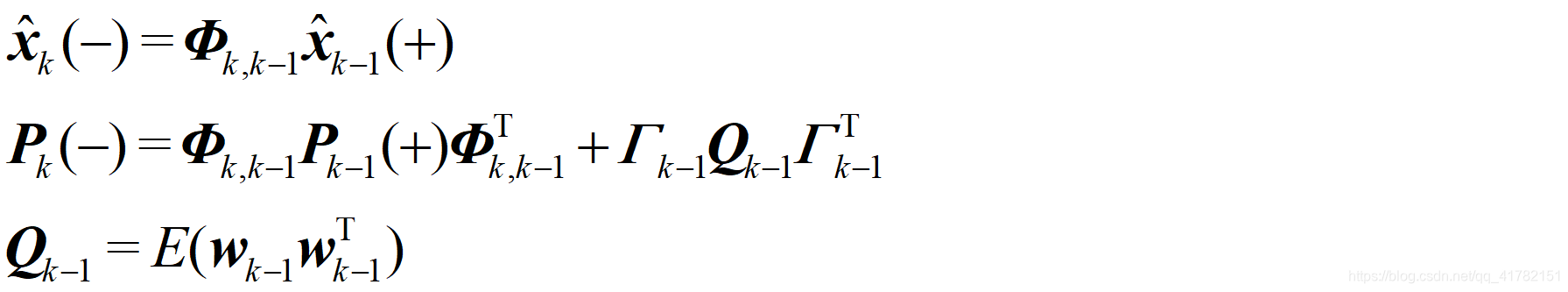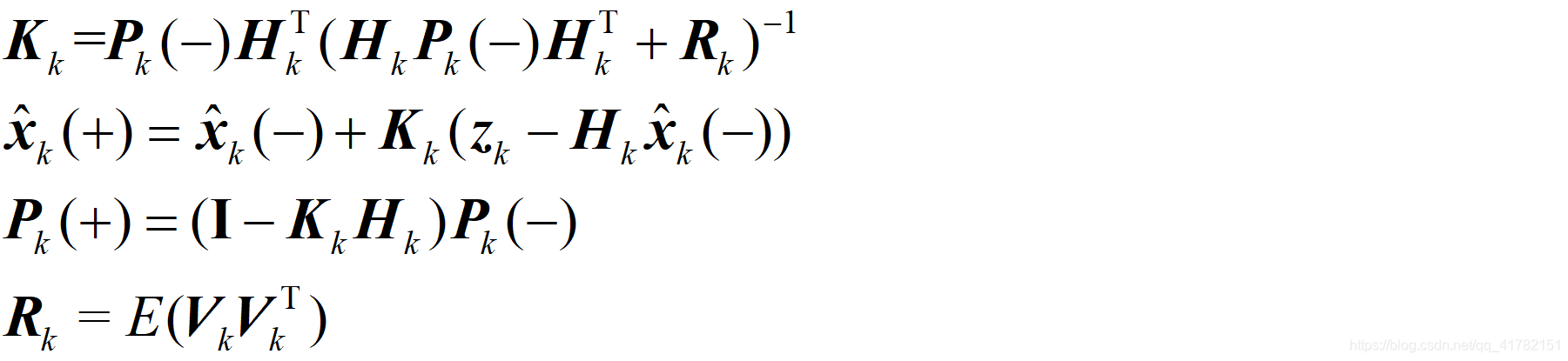前言

GNSS与INS具有很好的互补性，GNSS提供的位置结果不随时间发散，能够抑制惯导的误差累积，INS能在GNSS拒止环境下提供短时高精度的定位结果，GNSS/INS组合导航系统能充分发挥两系统的优势。与GNSS/INS紧组合系统相比，松组合的两个子系统相互不影响，拥有较强的稳定性，在车载组合导航领域应用广泛。本文简单整理了GNSS/INS松组合算法，里面参考了多本书籍并有些自己的理解，如若有误，还请告知一下，感激不尽。

GNSS/INS松组合状态模型

基于捷联惯导系统(SINS)误差模型，加入陀螺及加表的零偏白噪声wg，wa，陀螺及加表零偏建模为一阶马尔科夫过程，wcg，wca为对应的过程白噪声，INS误差模型可以整理如下：

根据上述模型，我们可以构建GNSS/INS松组合的状态模型：

GNSS/INS松组合量测模型

松组合系统采用n系（东北天）下SINS解算的位置与GNSS测量的位置之差作为量测信息，假设IMU到GNSS天线的杆臂向量为0，即GNSS天线与IMU的位置重合。

SINS解算的位置可表示为：

GNSS得到的位置可表示为：

则，位置量测：

转换到大地坐标系LLA（纬经高），得：

GNSS/INS松组合卡尔曼滤波

1、松组合模型离散化

2、卡尔曼滤波时间更新

3、卡尔曼滤波量测更新

注意我们这里的状态量是位置（姿态，速度）误差，将其补偿到位置（姿态，速度）量上后，误差就变为0了，所以这里的状态量要手动置零。