Bootstrap

C语言实现二叉树的四种遍历和求深度与叶子结点个数

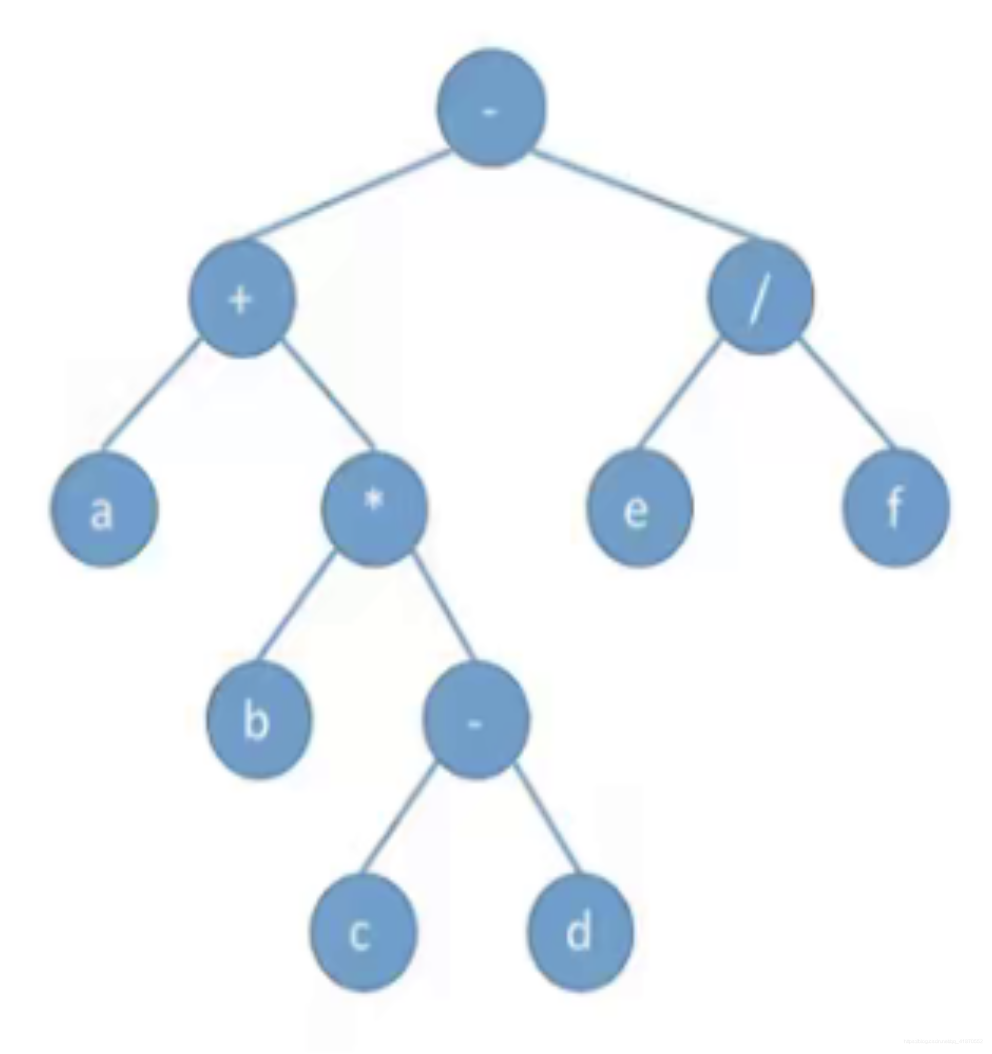
C语言实现二叉树的四种遍历和求深度与叶子结点个数

使用链式存储实现二叉树建立

1、定义存储数据类型和链式二叉树

//定义数据类型
typedef char ElemType;

//定义一个链式存储的二叉树结构
typedef struct BiTNode {
    ElemType data;
    struct BiTNode *lchild, *rchild;    //左右孩子指针
} BiTNode, *BiTree;

2、根据输入结点初始化并建立二叉树

//根据输入结点初始化并建立二叉树
bool CreateBiTree(BiTree &T) {
    //输入二叉树中的结点的值(一个字符)，空格字符表示空树并构造二叉链表表示的树T
    ElemType ch;
    scanf("%c", &ch);
    getchar();
    if (ch == ' ') {
        T = NULL;
    } else {
        if (!(T = (BiTree) malloc(sizeof(BiTNode)))) {
            return false;
        }
        T->data = ch;                    //生成根结点
        printf("请输入%c的左子树：", ch);
        CreateBiTree(T->lchild);        //构造左子树
        printf("请输入%c的右子树：", ch);
        CreateBiTree(T->rchild);        //构造右子树
    }
    return true;
}

构造访问输出Visit函数

//访问输出Visit函数
void Visit(BiTree T) {    //输出元素e的值
    printf("%c", T->data);
}

二叉树的先序遍历

//先序遍历二叉树T
void PreOrder(BiTree T) {
    //根左右
    if (T != NULL) {
        Visit(T);
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}

二叉树的中序遍历

//中序遍历二叉树T
void InOrder(BiTree T) {
    //左根右
    if (T != NULL) {
        InOrder(T->lchild);
        Visit(T);
        InOrder(T->rchild);
    }
}

二叉树的后序遍历

//后序遍历二叉树T
void PosOrder(BiTree T) {
    //左右根
    if (T) {
        PosOrder(T->lchild);
        PosOrder(T->rchild);
        Visit(T);
    }
}

求二叉树的深度和叶子结点个数

1、求二叉树的深度

//求树的深度
int TreeDeep(BiTree T) {
    int deep = 0;
    if (T != NULL) {
        int leftDeep = TreeDeep(T->lchild);
        int rightDeep = TreeDeep(T->rchild);
        deep = leftDeep >= rightDeep ? leftDeep + 1 : rightDeep + 1;
    }
    return deep;
}

2、求二叉树的叶子结点个数

//求树叶的个数
int LeafCount(BiTree T, int &num) {
    if (T) {
        if (T->lchild == NULL && T->rchild == NULL) {
            num++;
        }
        LeafCount(T->lchild, num);
        LeafCount(T->rchild, num);
    }
    return num;
}

定义顺序队列并初始化

1、定义一个顺序队列

//定义一个顺序队列（循环队列）用于层序遍历
typedef struct {
    BiTree BNode[MaxSize];  //用静态数组存放队列元素
    int front, rear;     //队头队尾指针，队尾指针指向队尾元素的下一个位置！
    //int size=0;   队列长度，初始为0,用此变量可以不牺牲一个存储单元
    //int tag;      删除操作tag置0，插入操作tag置1
} SqQueue;

2、初始化队列

//初始化顺序队列
void InitQueue(SqQueue &Q) {
    Q.front = Q.rear = 0;
}

构造队列相关函数

1、判断队列是否为空

//判断队列是否为空
bool IsEmpty(SqQueue Q) {
    if (Q.front == Q.rear)
        return true;
    else

2、队列入队操作

//顺序队列入队操作
bool EnQueue(SqQueue &Q, BiTree T) {
    if ((Q.rear + 1) % MaxSize == Q.front)  //判断队列是否已满
        return false;
//    if (Q.size==MaxSize)
//        return false;
    Q.BNode[Q.rear] = T;                 //先将新元素放进队尾指针的位置
    Q.rear = (Q.rear + 1) % MaxSize;    // 再将队尾指针加1对MaxSize取模
//    Q.size++;
    return true;
}

3、队列出队操作

//顺序队列出队操作
bool DeQueue(SqQueue &Q, BiTree &T) {
    if (Q.front == Q.rear)              //判断队列是否为空
        return false;
//    if (Q.size==0)
//        return false;
    T = Q.BNode[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
//    Q.size--;
    return true;
}

使用队列实现二叉树的层序遍历

//层序遍历二叉树T
void LevelOrder(BiTree T, SqQueue &Q) {
    //使用队列实现
    if (T != NULL) {
        EnQueue(Q, T);
    }
    while (IsEmpty(Q) == false) {
        BiTree T1;
        DeQueue(Q, T1);
        Visit(T1);
        if (T1->lchild != NULL)
            EnQueue(Q, T1->lchild);
        if (T1->rchild != NULL)
            EnQueue(Q, T1->rchild);
    }
}

整个项目的完整代码

//使用链实现求二叉树的先序遍历、中序遍历、后序遍历、树的深度和树的叶子结点个数
//使用队列实现二叉树的层序遍历
#include<stdio.h>
#include<stdlib.h>

//队列的最大长度
#define MaxSize 255

//定义数据类型
typedef char ElemType;

//定义一个链式存储的二叉树结构
typedef struct BiTNode {
    ElemType data;
    struct BiTNode *lchild, *rchild;    //左右孩子指针
} BiTNode, *BiTree;

//定义一个顺序队列（循环队列）用于层序遍历
typedef struct {
    BiTree BNode[MaxSize];  //用静态数组存放队列元素
    int front, rear;     //队头队尾指针，队尾指针指向队尾元素的下一个位置！
    //int size=0;   队列长度，初始为0,用此变量可以不牺牲一个存储单元
    //int tag;      删除操作tag置0，插入操作tag置1
} SqQueue;

//根据输入结点初始化并建立二叉树
bool CreateBiTree(BiTree &T) {
    //输入二叉树中的结点的值(一个字符)，空格字符表示空树并构造二叉链表表示的树T
    ElemType ch;
    scanf("%c", &ch);
    getchar();
    if (ch == ' ') {
        T = NULL;
    } else {
        if (!(T = (BiTree) malloc(sizeof(BiTNode)))) {
            return false;
        }
        T->data = ch;                    //生成根结点
        printf("请输入%c的左子树：", ch);
        CreateBiTree(T->lchild);        //构造左子树
        printf("请输入%c的右子树：", ch);
        CreateBiTree(T->rchild);        //构造右子树
    }
    return true;
}

//初始化顺序队列
void InitQueue(SqQueue &Q) {
    Q.front = Q.rear = 0;
}

//判断队列是否为空
bool IsEmpty(SqQueue Q) {
    if (Q.front == Q.rear)
        return true;
    else
        return false;
}

//顺序队列入队操作
bool EnQueue(SqQueue &Q, BiTree T) {
    if ((Q.rear + 1) % MaxSize == Q.front)  //判断队列是否已满
        return false;
//    if (Q.size==MaxSize)
//        return false;
    Q.BNode[Q.rear] = T;                 //先将新元素放进队尾指针的位置
    Q.rear = (Q.rear + 1) % MaxSize;    // 再将队尾指针加1对MaxSize取模
//    Q.size++;
    return true;
}

//顺序队列出队操作
bool DeQueue(SqQueue &Q, BiTree &T) {
    if (Q.front == Q.rear)              //判断队列是否为空
        return false;
//    if (Q.size==0)
//        return false;
    T = Q.BNode[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
//    Q.size--;
    return true;
}

//访问输出Visit函数
void Visit(BiTree T) {    //输出元素e的值
    printf("%c", T->data);
}

//先序遍历二叉树T
void PreOrder(BiTree T) {
    //根左右
    if (T != NULL) {
        Visit(T);
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}

//中序遍历二叉树T
void InOrder(BiTree T) {
    //左根右
    if (T != NULL) {
        InOrder(T->lchild);
        Visit(T);
        InOrder(T->rchild);
    }
}

//后序遍历二叉树T
void PosOrder(BiTree T) {
    //左右根
    if (T) {
        PosOrder(T->lchild);
        PosOrder(T->rchild);
        Visit(T);
    }
}

//层序遍历二叉树T
void LevelOrder(BiTree T, SqQueue &Q) {
    //使用队列实现
    if (T != NULL) {
        EnQueue(Q, T);
    }
    while (IsEmpty(Q) == false) {
        BiTree T1;
        DeQueue(Q, T1);
        Visit(T1);
        if (T1->lchild != NULL)
            EnQueue(Q, T1->lchild);
        if (T1->rchild != NULL)
            EnQueue(Q, T1->rchild);
    }
}

//求树的深度
int TreeDeep(BiTree T) {
    int deep = 0;
    if (T != NULL) {
        int leftDeep = TreeDeep(T->lchild);
        int rightDeep = TreeDeep(T->rchild);
        deep = leftDeep >= rightDeep ? leftDeep + 1 : rightDeep + 1;
    }
    return deep;
}

//求树叶的个数
int LeafCount(BiTree T, int &num) {
    if (T) {
        if (T->lchild == NULL && T->rchild == NULL) {
            num++;
        }
        LeafCount(T->lchild, num);
        LeafCount(T->rchild, num);
    }
    return num;
}

int main() {
    BiTree T;
    SqQueue Q;
    InitQueue(Q);
    int num = 0;
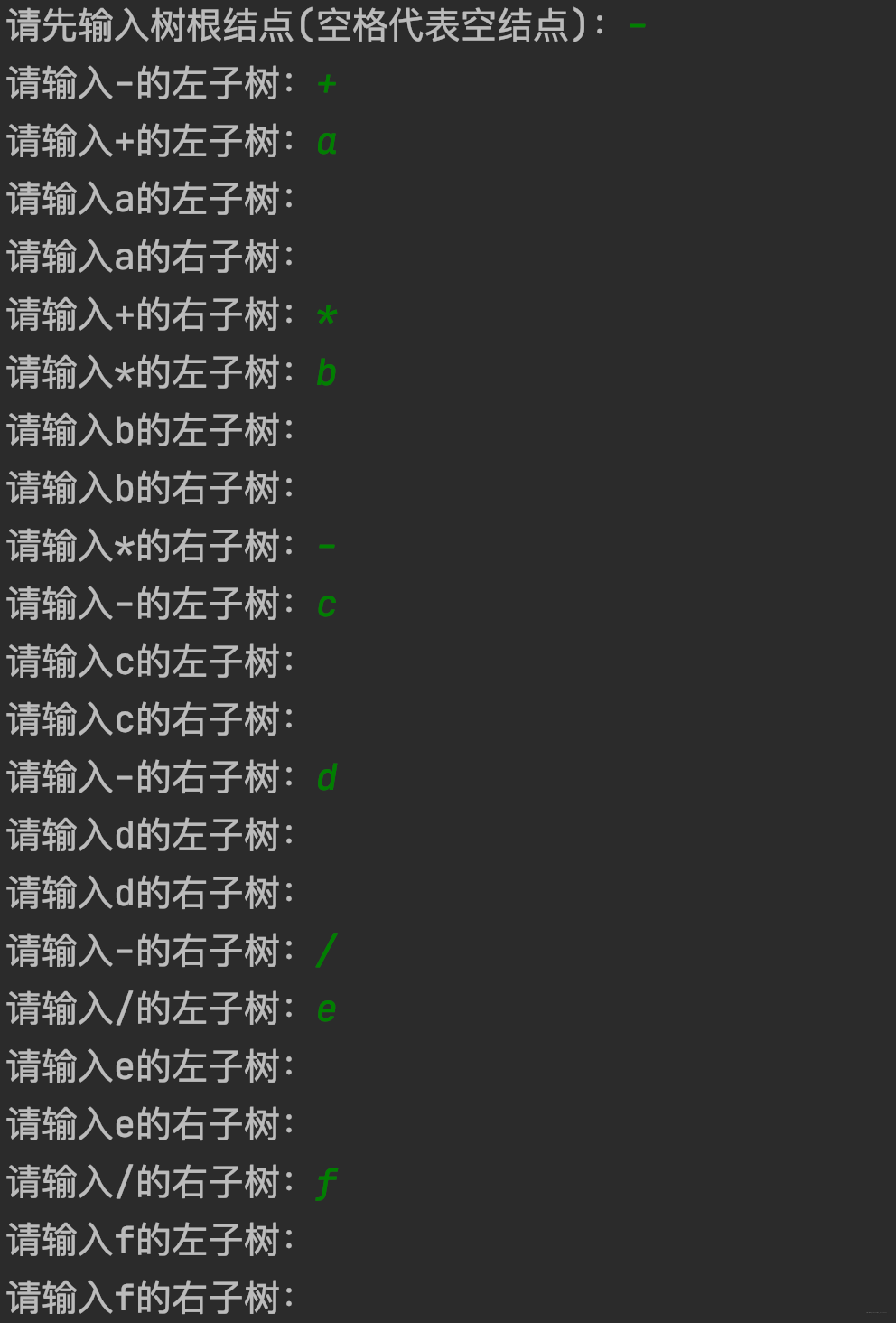
    printf("请先输入树根结点(空格代表空结点)：");
    CreateBiTree(T);
    printf("该二叉树的先序遍历结果为：");
    PreOrder(T);
    printf("\n");
    printf("该二叉树的中序遍历结果为：");
    InOrder(T);
    printf("\n");
    printf("该二叉树的后序遍历结果为：");
    PosOrder(T);
    printf("\n");
    printf("该二叉树的层次遍历结果为：");
    LevelOrder(T, Q);
    printf("\n");
    printf("该二叉树的深度为:");
    printf("%d\n", TreeDeep(T));
    printf("该二叉树的叶子结点个数为:");
    printf("%d\n", LeafCount(T, num));
    return 0;
}

运行效果图

a+b*(c-d)-e/f
在这里插入图片描述
在这里插入图片描述

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
安装Vim出错，显示Cannot find a valid baseurl for repo: base/7/x86_64
C语言——函数递归
计算机毕业设计 php分享网站 毕设
MFC 鼠标悬停在控件上，显示提示信息
线程池超载求生指南：四大拒绝策略应对并发挑战（Java线程池拒绝策略全解析）
二维数组初始化和遍历
在Unity3D中的渲染优化-减少需要处理的顶点数目
HMSC联合物种分布模型在群落生态学中的贝叶斯统计分析
基于python+flask框架的晋中学院校友信息管理系统（开题+程序+论文） 计算机毕设
Recurrent Dynamic Embedding for Video Object Segmentation
;