本期我们讲解基数排序,基数排序讲完后,我们的常用排序算法专栏就已经讲完了,后续可能会出一些排序优化问题,以及排序算法结合C语言实战,比如迷宫求解、🅿停车场系统、机房预约系统以及植物大战僵尸外挂等等小项目。本人从零开始学习云计算的专栏也在不断更新中,喜欢的小伙伴可以继续关注。
🥒一、基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或binsort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,在某些时候,基数排序法的效率高于其它的稳定性排序法。
🍉二、排序思想
💉基数排序就是桶排序,也可以说是桶排序的一种,基数排序固定式九个桶,分别对应的是0~9十个数字。
基数排序的基本思想是:先将待排序序列按个位数排好,然后按顺序复制回原数组;再按十位排序好,再按顺序复制回原数组;依次类推,按百位、千位,排序的趟数就是最大数的位数,比如千位数就要排四趟,百位数就要排3趟。
🥭三、动图演示
我们先来看看基数排序的动图演示,一定要格外注意,把桶里面的数组放回去时,有些桶只有一个数,有些桶有多个数,而这些多个数的桶,他的数据放回去时,是按照放下来的顺序放回去的,也就是先下来的先上去这点很重要,🙉🙉后面要考。
🍍四、图解
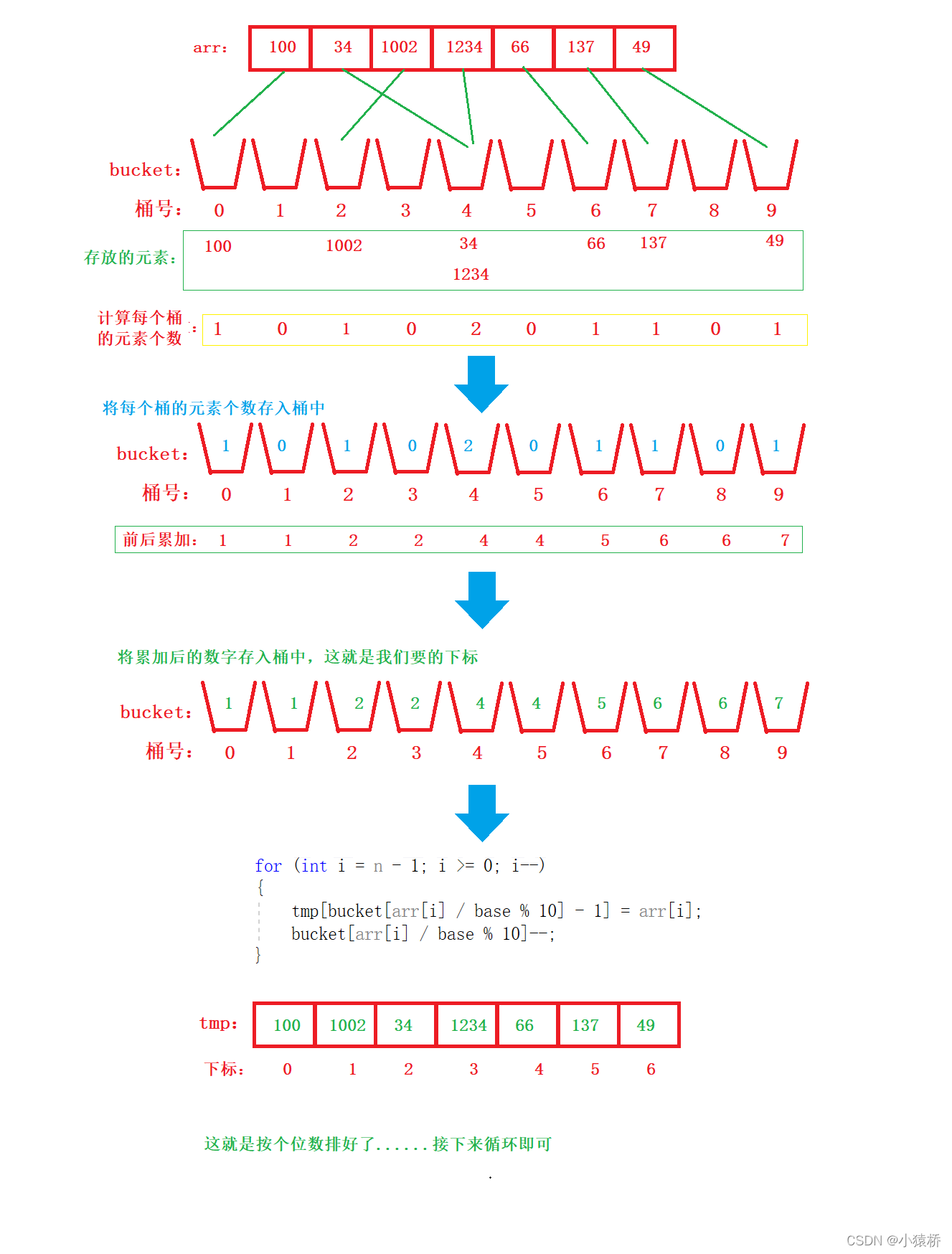
看了上面的动图,是不是感觉基数排序的思想及其简单,但是代码却是极为不好写,很复杂。因为我们得弄清楚,桶里面到底装的是什么,是数据本身吗?如果不是,数据本身存放在哪里?让我们接着往下看👇👇👇👇
接下来讲解一下上图是什么意思。因为我们是按数据的每一位进行排序,所以我们就得定义九个桶,根据数据的位值,将待排序的序列按位值丢进桶里面(但不是真的丢进去),上图中我们已经将数据按照各位丢进了各自的桶中,这时候我们只需要按顺序将这些数据再次放回原数组就可以了,但是,怎么放?这个顺序怎么找,很明显,我们得借助一个临时数组,这个临时数组和原数组等长,用来先存放这些要归还的数据。现在我们就需要将这些数从后往前放到临时数组(为什么要从后往前后面会剖析),到底要怎么放?👀👀拿上面的例子举例,我们可以提前知道,最后放进临时数组的顺序是这样的
我们从49开始放,现在我们只需要知道49的下标是几,就能够把数据精准的放进去,那么49的下标6是怎么来的呢?很简单,因为49的前面有六个数啊,哈哈哈,是不是很简单?那么,这六个数的6怎么得来?🌝🌝🌝🌝
| 🥕🥕答案就是:先统计每个桶里面有多少个数,这是真正要放在桶里面的数据,然后前后累加,每个桶里面的元素就代表着累计加起来总共有多少个数。将这个数减去1就可以得到每个数该放到临时数组的下标。 | |
🍓五、代码实现(包含详细注释)
//基数排序
void RadixSort(int* arr, int n)
{
//max为数组中最大值
int max = arr[0];
int base = 1;
//找出数组中的最大值
for (int i = 0; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
}
//循环结束max就是数组最大值
//临时存放数组元素的空间
int* tmp = (int*)malloc(sizeof(int)*n);
//循环次数为最大数的位数
while (max / base > 0)
{
//定义十个桶,桶里面装的不是数据本身,而是每一轮排序对应(十、白、千...)位的个数
//统计每个桶里面装几个数
int bucket[10] = { 0 };
for (int i = 0; i < n; i++)
{
//arr[i] / base % 10可以取到个位、十位、百位对应的数字
bucket[arr[i] / base % 10]++;
}
//循环结束就已经统计好了本轮每个桶里面应该装几个数
//将桶里面的元素依次累加起来,就可以知道元素存放在临时数组中的位置
for (int i = 1; i < 10; i++)
{
bucket[i] += bucket[i - 1];
}
//循环结束现在桶中就存放的是每个元素应该存放到临时数组的位置
//开始放数到临时数组tmp
for (int i = n - 1; i >= 0; i--)
{
tmp[bucket[arr[i] / base % 10] - 1] = arr[i];
bucket[arr[i] / base % 10]--;
}
//不能从前往后放,因为这样会导致十位排好了个位又乱了,百位排好了十位又乱了
/*for (int i = 0; i < n; i++)
{
tmp[bucket[arr[i] / base % 10] - 1] = arr[i];
bucket[arr[i] / base % 10]--;
}*/
//把临时数组里面的数拷贝回去
for (int i = 0; i < n; i++)
{
arr[i] = tmp[i];
}
base *= 10;
}
free(tmp);
}
🍒六、问题解答
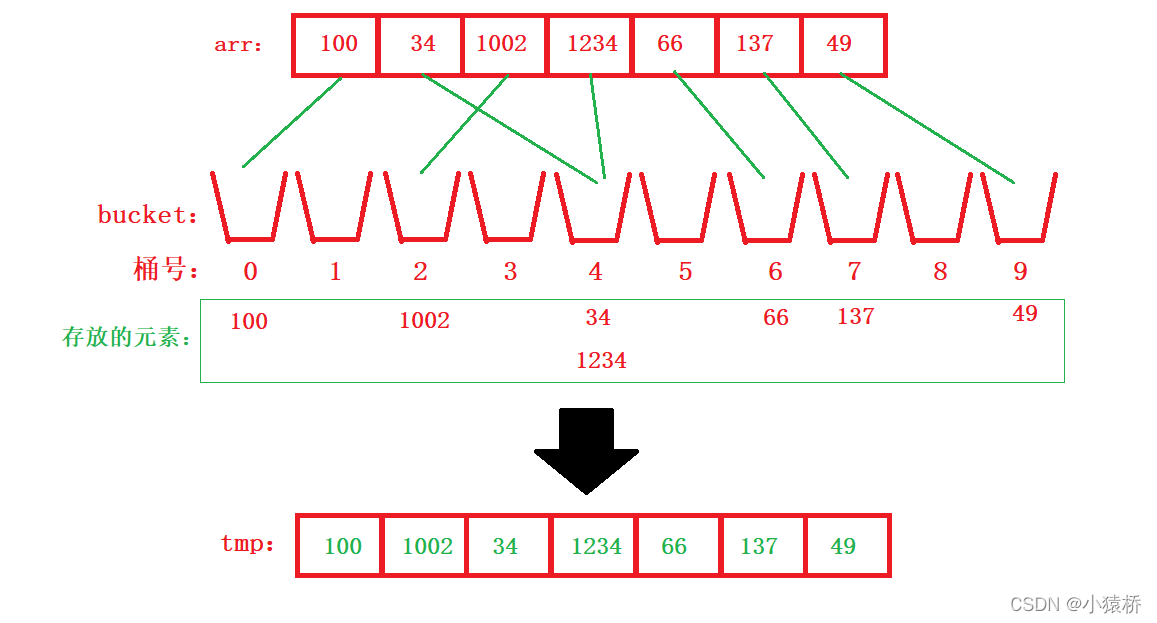
我们解答一下前面一直强调的问题,将数据放到临时数组时为什么要从后往前放。我们来看看,
🌲🌲对于这个数组,我们按各位排完的顺序应该是如上图所示,对于四号桶,先排的34,后排的1234,因为34先被拿下来,但如果我们从前往后排,就会导致1234在前,34在后,因为我们代码是这样写的,i先扫到的元素会放到后面一个位置,bucket[arr[i] / base % 10]再减减,减减之后就是前一个位置了。意思就是,我们早就已经为四号桶准备了两个位置放置元素,谁先放,就会被放到下标大的那个位置。所以我们从后往前放,就能将本应该放到下标大的位置的1234放到它正确的位置上。
//开始放数到临时数组tmp
for (int i = n - 1; i >= 0; i--)
{
tmp[bucket[arr[i] / base % 10] - 1] = arr[i];
bucket[arr[i] / base % 10]--;
}
🍇七、致命缺陷(负数问题)
我们当前的程序只能排正数,一旦出现负数,程序就崩了。我们如何解决呢?
| 🌈💨答案就是:既然出现了负数,我们只需要将所有的数加上一个数,把所有的数变为非负数即可。那么这个数是什么呢?没错,就是数组里面最小数的绝对值,加上这个数后,排完序再将这个数给它减掉即可。 | |
优化后的代码为:
//基数排序
void RadixSort(int* arr, int n)
{
//max为数组中最大最小值
int max = arr[0];
int min = arr[0];
int base = 1;
//找出数组中的最大值
for (int i = 0; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
//循环结束max就是数组最大最小值
//循环将数组的元素全部变为正数
//所有元素加上最小值的绝对值
for (int i = 0; i < n; i++)
{
arr[i] += abs(min);
}
//临时存放数组元素的空间
int* tmp = (int*)malloc(sizeof(int)*n);
//循环次数为最大数的位数
while (max / base > 0)
{
//定义十个桶,桶里面装的不是数据本身,而是每一轮排序对应(十、白、千...)位的个数
//统计每个桶里面装几个数
int bucket[10] = { 0 };
for (int i = 0; i < n; i++)
{
//arr[i] / base % 10可以取到个位、十位、百位对应的数字
bucket[arr[i] / base % 10]++;
}
//循环结束就已经统计好了本轮每个桶里面应该装几个数
//将桶里面的元素依次累加起来,就可以知道元素存放在临时数组中的位置
for (int i = 1; i < 10; i++)
{
bucket[i] += bucket[i - 1];
}
//循环结束现在桶中就存放的是每个元素应该存放到临时数组的位置
//开始放数到临时数组tmp
for (int i = n - 1; i >= 0; i--)
{
tmp[bucket[arr[i] / base % 10] - 1] = arr[i];
bucket[arr[i] / base % 10]--;
}
//不能从前往后放,因为这样会导致十位排好了个位又乱了,百位排好了十位又乱了
/*for (int i = 0; i < n; i++)
{
tmp[bucket[arr[i] / base % 10] - 1] = arr[i];
bucket[arr[i] / base % 10]--;
}*/
//把临时数组里面的数拷贝回去
for (int i = 0; i < n; i++)
{
arr[i] = tmp[i];
}
base *= 10;
}
free(tmp);
//还原原数组
for (int i = 0; i < n; i++)
{
arr[i] -= abs(min);
}
}