公式
向量形式
x
i
(
k
)
=
∑
j
∈
N
(
i
)
∪
{
i
}
1
deg
(
i
)
⋅
d
e
g
(
j
)
⋅
(
Θ
⋅
x
j
(
k
−
1
)
)
,
\mathbf{x}_i^{(k)} = \sum_{j \in \mathcal{N}(i) \cup \{ i \}} \frac{1}{\sqrt{\deg(i)} \cdot \sqrt{deg(j)}} \cdot \left( \mathbf{\Theta} \cdot \mathbf{x}_j^{(k-1)} \right),
xi(k)=j∈N(i)∪{i}∑deg(i)⋅deg(j)1⋅(Θ⋅xj(k−1)),
其中,
Θ
\mathbf{\Theta}
Θ是权重矩阵(即机器学习中要更新的参数),
x
i
(
k
)
\mathbf{x}_i^{(k)}
xi(k)表示节点
i
i
i第
k
k
k次迭代的特征向量,
d
e
g
(
i
)
{deg(i)}
deg(i)表示节点
i
i
i的度,
N
(
i
)
\mathcal{N}(i)
N(i)表示节点
i
i
i的所有邻居节点的集合。
矩阵形式
X
′
=
D
^
−
1
/
2
A
^
D
^
−
1
/
2
X
Θ
\mathbf{X}^{\prime} = \mathbf{\hat{D}}^{-1/2} \mathbf{\hat{A}} \mathbf{\hat{D}}^{-1/2} \mathbf{X} \mathbf{\Theta}
X′=D^−1/2A^D^−1/2XΘ
为了便于理解,我后面有些地方用向量形式,有些地方用矩阵形式。
GCNConv源码
目前最新版本的源码已经和下面的代码不一样了,但是原理基本上是一样的。
import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super(GCNConv, self).__init__(aggr='add') # "Add" aggregation.
self.lin = torch.nn.Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# x has shape [N, in_channels]
# edge_index has shape [2, E]
# Step 1: Add self-loops to the adjacency matrix.
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# Step 2: Linearly transform node feature matrix.
x = self.lin(x)
# Step 3-5: Start propagating messages.
return self.propagate(edge_index, size=(x.size(0), x.size(0)), x=x)
def message(self, x_j, edge_index, size):
# x_j has shape [E, out_channels]
# edge_index has shape [2, E]
# Step 3: Normalize node features.
row, col = edge_index
deg = degree(row, size[0], dtype=x_j.dtype) # [N, ]
deg_inv_sqrt = deg.pow(-0.5) # [N, ]
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
return norm.view(-1, 1) * x_j
def update(self, aggr_out):
# aggr_out has shape [N, out_channels]
# Step 5: Return new node embeddings.
return aggr_out
初始化init
这一部分主要是定义了一个线性变换的结构进行降维。
def __init__(self, in_channels, out_channels):
super(GCNConv, self).__init__(aggr='add') # "Add" aggregation.
self.lin = torch.nn.Linear(in_channels, out_channels)
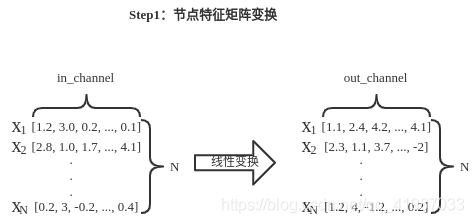
其中in_channels是节点特征的维度,out_channels是我们自己设定的降维维度。这里只是定义了结构,具体的逻辑实现是在forward()里实现的。这一部分对应着
X
Θ
\mathbf{X} \mathbf{\Theta}
XΘ。输入维度为(N, in_channels),输出维度为(N, out_channels)。N是节点个数。
forward
def forward(self, x, edge_index):
# x has shape [N, in_channels]
# edge_index has shape [2, E]
# Step 1: Add self-loops to the adjacency matrix.
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# Step 2: Linearly transform node feature matrix.
x = self.lin(x)
# Step 3-5: Start propagating messages.
return self.propagate(edge_index, size=(x.size(0), x.size(0)), x=x)
-
1、给邻接矩阵加上自循环,也即构造出矩阵 A ^ \mathbf{\hat{A}} A^
但是如果用边的形式表示的话,相当于在原先的数组上加上source和target节点编号相同的边。例如,从[[0,1,1,2],[1,0,2,1]]变成了[[0,1,1,2,0,1,2],[1,0,2,1,0,1,2]] -
2、实现了线性变换
如在init里所说的一样。
message
def message(self, x_j, edge_index, size):
# x_j has shape [E, out_channels]
# edge_index has shape [2, E]
# Step 3: Normalize node features.
row, col = edge_index
deg = degree(row, size[0], dtype=x_j.dtype) # [N, ]
deg_inv_sqrt = deg.pow(-0.5) # [N, ]
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
return norm.view(-1, 1) * x_j
- 3、对特征进行归一化
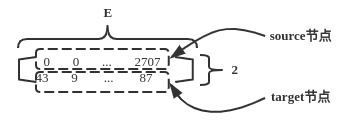
首先说明x_j的由来。这里E表示边的个数,
对边矩阵edge_index,形状为(2, E),第一行表示边的source节点(在代码中是row,这两者在本文中等价),第二行表示边的target节点(在代码中是col,这两者在本文中等价),如下示意图
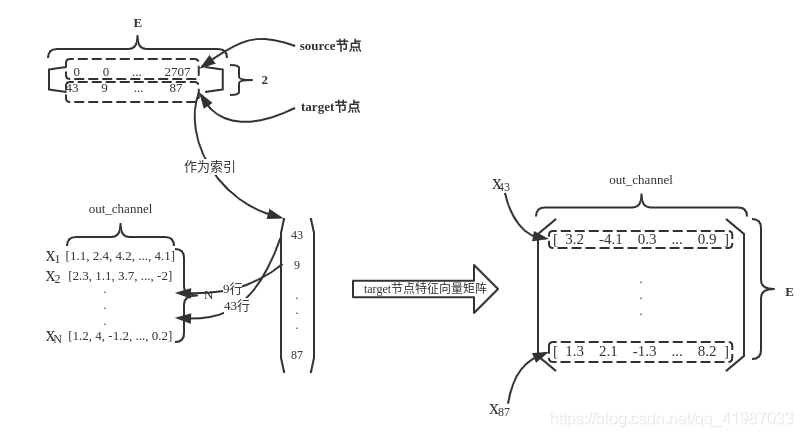
然后,以target节点作为索引,从线性变换后的特征矩阵中索引得到target节点的特征矩阵,示意图如下
这就是x_j的由来,也是为什么形状为(E, out_channels)的原因。这一部并未在上面的代码中体现,我也是看别人的文章才知道的。
在message函数中,首先计算了row(target)的度,这里默认图是无向图,row的度和col的度在结果上是一样的。deg[0]表示编号为0的节点的度,因此它的长度为N。而deg_inv_sqrt[row]返回了长度为E的度数组。例如,deg_inv_sqrt[0]表示第1条边的source的度的开根号,因此若把它与第一条边的target的度的开根号,就能得到标准化系数了。因此,norm最终保存了所有边的标准化系数。
函数最后返回的是每一条边的标准化系数 × 这条边target这一端的节点特征
- 4、对邻居节点特征进行聚合操作
根据前面的数学公式
∑ j ∈ N ( i ) ∪ { i } 1 deg ( i ) ⋅ d e g ( j ) ⋅ ( Θ ⋅ x j ( k − 1 ) ) \sum_{j \in \mathcal{N}(i) \cup \{ i \}} \frac{1}{\sqrt{\deg(i)} \cdot \sqrt{deg(j)}} \cdot \left( \mathbf{\Theta} \cdot \mathbf{x}_j^{(k-1)} \right) j∈N(i)∪{i}∑deg(i)⋅deg(j)1⋅(Θ⋅xj(k−1))
可以看到累加是有条件的。对于节点i,我们只需要节点i本身以及它的邻居节点j就可以了。
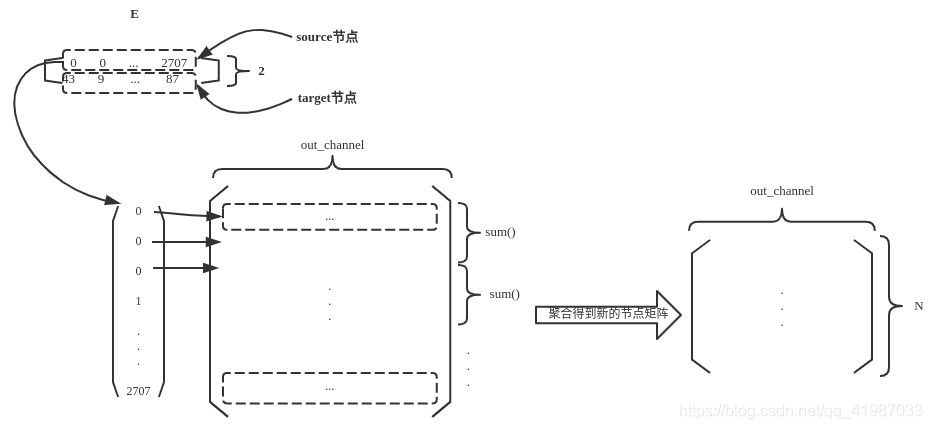
因此,在第3步所做的工作中,我们只需要找出source为i的特征向量并进行聚合即可。换句话说,按照source进行聚合,如下图所示
这里有3条边的source都是节点0,因此将这三行向量聚合(相加sum,取均值mean,取最大值max都可以,这里用相加),最终得到一个形状为(N, out_channels)的特征矩阵。该矩阵,就是这一层GCN的输出。
update
def update(self, aggr_out):
# aggr_out has shape [N, out_channels]
# Step 5: Return new node embeddings.
return aggr_out
- 5、直接返回信息聚合的输出
前向传播demo
demo使用pytorch geometric样例的图形,如下图所示
首先定义一张图。为了更好地理解,图中我把节点的特征值改成2维的了(而不是上面一样每个节点只有1维特征值)
import torch
from torch_geometric.data import Data
from torch_geometric.nn import GCNConv
# 随机种子
torch.manual_seed(0)
# 定义边
edge_index = torch.tensor([[0, 1, 1, 2],
[1, 0, 2, 1]], dtype=torch.long)
# 定义节点特征,每个节点特征维度是2
x = torch.tensor([[-1,2], [0,4], [1,5]], dtype=torch.float)
#创建一层GCN层,并把特征维度从2维降到1维
conv = GCNConv(2, 1)
# 前向传播
x = conv(x, edge_index)
print(x)
# tensor([[2.0028],
# [3.1795],
# [3.1302]], grad_fn=<AddBackward0>)
接下来我要手动计算最终结果是如何出来的。
-
1、添加自循环
输入:[[0,1,1,2],[1,0,2,1]],输出:[[0,1,1,2,0,1,2],[1,0,2,1,0,1,2]]。这个没什么好说的 -
2、线性变换降维
这里权重矩阵是随机生成的,和我的随机数种子有关,如果你们的随机数种子和我一样的话,结果也应该和我一样。
特征矩阵X=[[-1,2],[0,4],[1,5]]权重矩阵W=[[-0.0106], [0.7586]],因此XW=[[1.5279],[3.0346],[3.7826]](这是我在调试时得到的结果,因为权重矩阵后面还有小数没显示出来,如果你们手动计算的话会发现XW=[[1.5278],[3.0344],[3.7824]],后面也会有类似的问题,读者不用太过在意) -
3、特征归一化
source(代码中的row)=[0,1,1,2,0,1,2],target(代码中的col)=[1,0,2,1,0,1,2],度deg=[2,3,2],对度的数组取-0.5次幂得到deg_inv_sqrt=[0.7071, 0.5774, 0.7071]。有了上面这些信息,我们可以计算每一条边的归一化系数,计算方法是norm[0]=dev_inv_sqrt[row[0]] * dev_inv_sqrt[col[0]]=0.4082,即第一条边的归一化系数是0.4082。类似地,整个数组norm=deg_inv_sqrt[row] * deg_inv_sqrt[col]=[0.4082,0.4082,0.4082,0.4082,0.5000,0.3333,0.5000]
以source节点作为索引(我前面分析的时候用的是target作为索引,但是实际运行程序的时候默认是以source作为索引的,因此我按照这个来,上面的分析也暂时不改了),从线性变换后的特征矩阵中索引得到source节点的特征矩阵。
因此,根据source=[0,1,1,2,0,1,2]和XW=[[1.5279],[3.0346],[3.7826]],可以得到矩阵x_j=[[1.5279],[3.0346],[3.0346],[3.7826],[1.5279],[3.0346],[3.7826]],将该矩阵与norm对位相乘,得到src=[[0.6238],[1.2389],[1.2389],[1.5443],[0.7639],[1.0115],[1.8913]] -
4、聚合
聚合的意思,就是对于节点i,把它自身的特征向量和它周围所有节点j的特征向量相加(或平均,或取最大值)。根据target=[1,0,2,1,0,1,2]和src=[[0.6238],[1.2389],[1.2389],[1.5443],[0.7639],[1.0115],[1.8913]],把target中节点编号相同的索引所对应的src中特征向量相加。首先找0号节点,在target中索引是1和4,因此把src[1]和src[4]相加,得到0号节点的新特征值2.0028,1号节点和2号节点也进行类似的操作,最终得到输出[[2.0028], [3.1795],[3.1302]]。这一层图卷积层的前向传播就结束了。 -
5、更新
直接返回值。
参考文档
https://github.com/LYuhang/GNN_Review
https://blog.csdn.net/NockinOnHeavensDoor/article/details/88974568