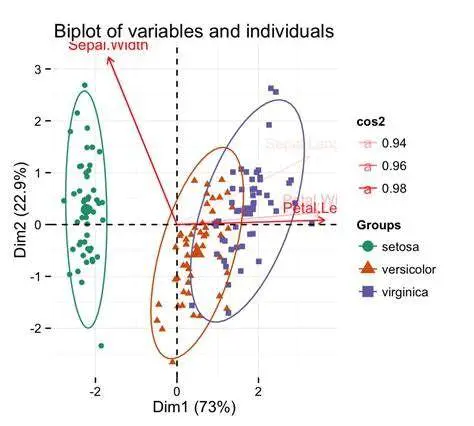
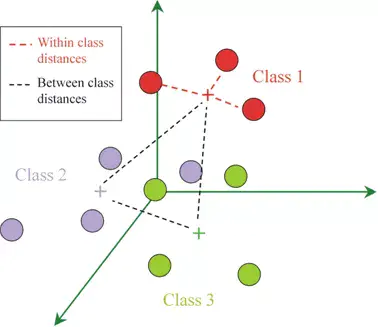
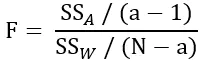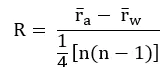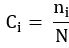常规的T检验、方差分析等，可以用于比较组间变量的差异水平。由于这些常规方法都是对于1-2个特定变量而言的，那么如果我们想比较所有变量整体的差异，或者说各组对象间在变量组成上是否存在较大的不同，应该怎样做呢？多变量情形下，可能会首先想到使用PCA等排序分析方法去降维，然后在低维空间的排序图中观测对象的离散程度，组间区分是否明显等。然后我们首先看下面这个PCA。排序图中，显示setosa与virginica或versicolor之间区分明显，virginica和versicolor之间存在一定程度的重叠。这种组间的区分程度是我们直接通过眼睛观测的，那么，通过观测的评估是否是准确的？比方说，setosa与virginica或versicolor之间在变量组成上是否真的存在显著差异呢？类似地，virginica和versicolor在PCA图中区分不明显，那么它们真的无区别吗（是否存在潜在差异）？

image

由于PCA只是探索性分析，用于描述数据分布，不涉及统计检验，因此无法给出一个指标（如p值）作为我们评估组间差异程度的标准。尽管很多情况下可能并不需要，但如果存在必要，我们还需结合其它方法用作评估。

这里就需要考虑特定的统计检验方法，用作组间差异分析。

对于多变量情形下的组间差异分析，可能首先会想到多元方差分析（MANOVA）。然而，MANOVA的有效性取决于严格的前提假设，如多元正态性、方差-协方差矩阵的同质性等，导致在实际情况中大部分案例都是直接拒绝的，因此MANOVA不具普适性。考虑到这一点，统计学家们已经提出了许多方法替代经典的MANOVA，它们在比较多变量的组时更为稳健，并得到了广泛应用。

其中一些方法并非直接通过原始的变量作比较，而是首先基于多变量计算对象间的“距离”，然后将距离测度用作检验的输入，进而确定各组对象间的差异程度。这类方法通常称为“基于距离的检验方法”（Distance‐Based Tests），常见的如置换多元方差分析（PERMANOVA）、相似性分析（ANOSIM）、Mantel test等。

好了，到这里就开始接本篇的正文部分了，简单地对这些常见的基于距离的检验方法作个概述。

上文描述通过PCA这个示例，仅为引出“基于距离的检验方法”这个概念，以加深大家对这种方法的印象。请允许我以这种方式作为本篇的开头，尽管降维排序与统计检验是相互独立的两种统计方法。

实际的比较分析中，这种基于距离的检验方法也并不总和PCA这些降维分析结合在一起。如上所述，在分析变量间的差异后，期望通过全局变量水平评估对象间的区别，这是它们常出现的应用场景。

PERMANOVA

首先是最广为熟知的置换多元方差分析（Permutational multivariate analysis of variance，PERMANOVA），又称非参数多因素方差分析（nonparametric multivariate analysis of variance），或者ADONIS分析，其基于伪F值的置换检验，通过对两组或两组以上对象距离平方和的分解检验它们之间有无差异的非参数方法（Anderson, 2001）

PERMANOVA计算过程概括如下：

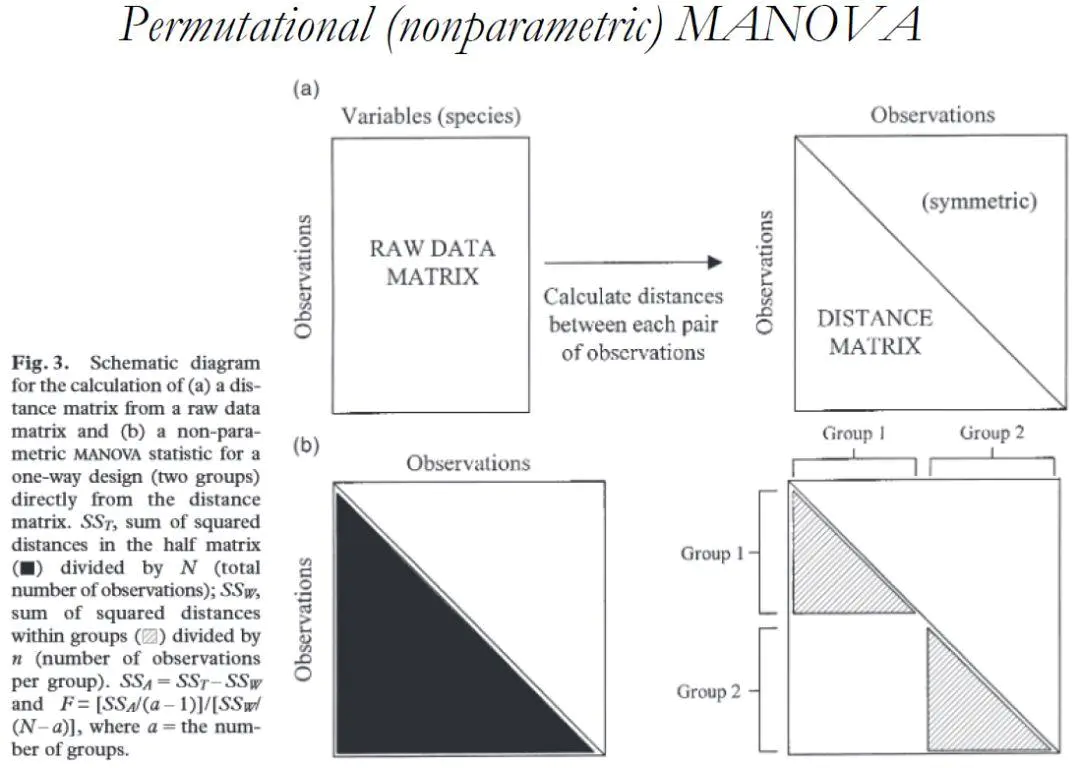
（1）根据变量组成信息，计算对象间的距离；

（2）计算所有对象的平均距离（SST）；

（3）计算组内对象之间的平均距离（SSW）；

（4）计算组间的平均距离（SSA= SST - SSW）；

（5）计算F值，式中N为数据集中的对象总数，a为分组数量。

image

image

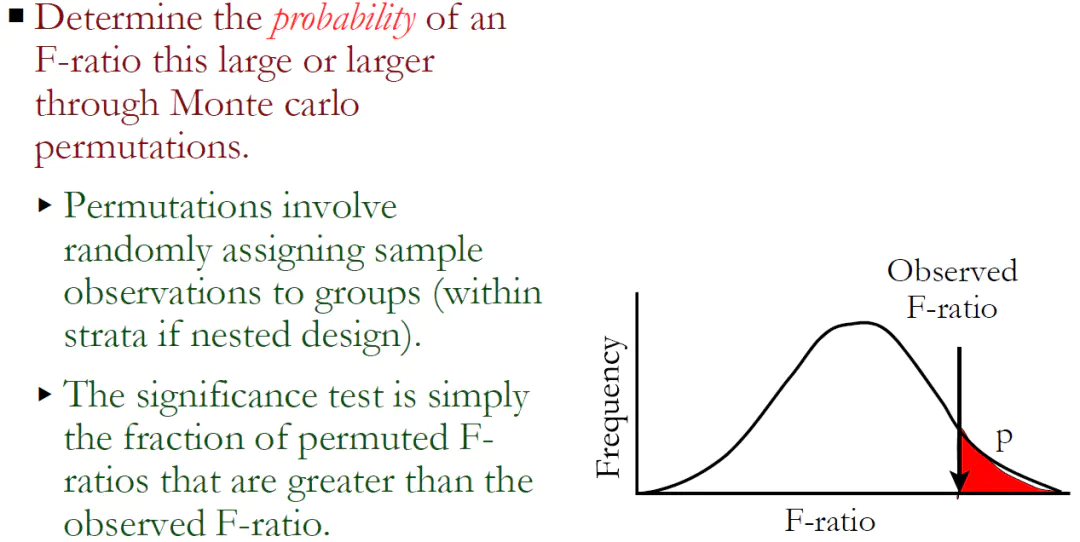
之后通过随机置换的方式，计算置换后数据的伪F值。多次置换后，伪F值大于观测F值的概率即为p值。p值即代表了检验的显著性信息，p越低越显著。

image

ANOSIM

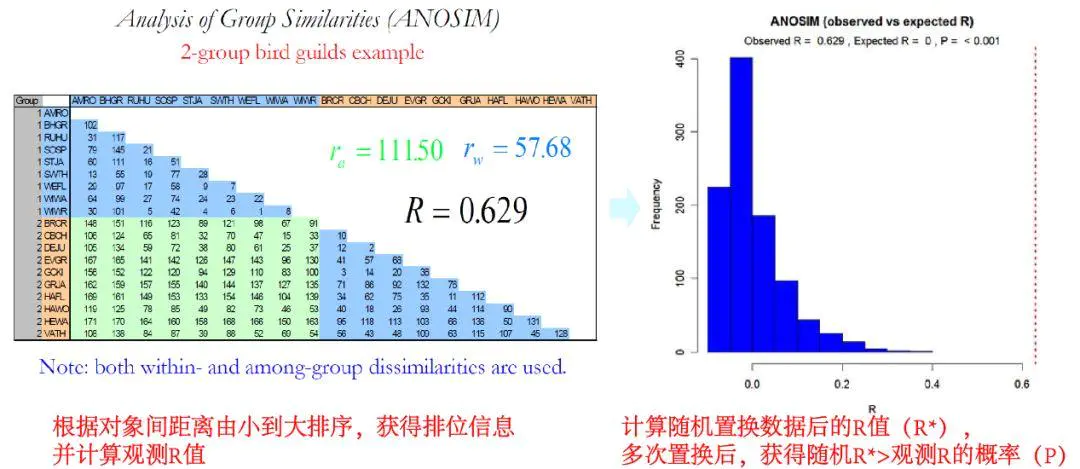
相似性分析（Analysis of similarities，ANOSIM）是一种用于分析高维度数据组间相似性的非参数检验方法，它通过检验组间的差异是否显著大于组内差异，评判目标分组是否有意义（Clark, 1993）。

image

首先根据变量组成信息，计算对象间的距离，将所有距离从小到大进行排序后（最小距离的对象距离排位1，以此类推）计算R值。R值可以得出组间与组内比较的差异程度，其取值范围（-1，1）；R>0，说明组间差异大于组内差异，即组间差异显著；R<0，说明组内差异大于组间差异；R值的绝对值越大表明相对差异越大。

计算如下，其中，r<sub>a</sub>为组间（Among groups，或称Between groups）距离排位的平均值，rw为组内（Within groups）距离排位的平均值，n为测试的对象总数。

image

之后通过随机置换的方式，计算置换后数据的R值（R）。多次置换后，随机R大于观测R值的概率即为p值。p值即代表了检验的显著性信息，p越低表明越容易接受观测R值，ANOSIM结果越可信。

image

Mantel test

尽管Mantel test通常用于确定两个距离矩阵的相关性，但也可用于检验假设或模型。通过在模型矩阵中比较组间距离与组内距离的差异程度，用以确定分组是否显著。此时Mantel test和ANOSIM的工作方式相似，但其特殊形式在于，为模型矩阵选择的特定值是根据距离数值本身而非根据排位确定的。

如下概括了Mantel test确定分组差异的方法（而非相关性，对于Mantel test确定两矩阵间相关性的方法，可参考前文）。

image

MRPP

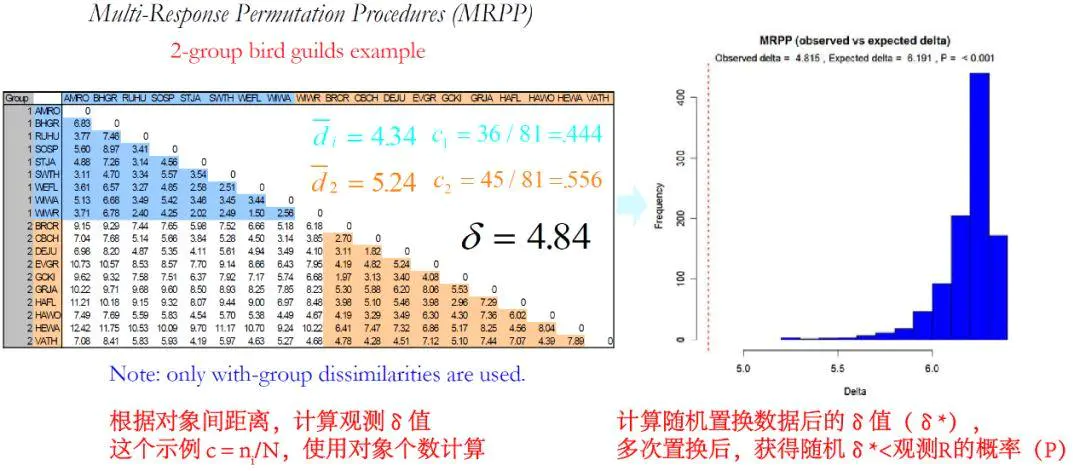
MRPP（Multi Response Permutation Procedure）基于组内和组间差异的置换检验，确定两组或两组以上数据集有无差异的非参数过程（Mielke, 1976）。

首先根据变量组成信息，计算对象间的距离，并计算各组内对象间的平均距离（`di），之后计算δ值（组内距离的加权平均）。下式中g为总分组的数量；ni表示第i个分组的对象数量，N为数据集中的总对象数量；注意有的公式中n和N使用自由度（即对象数量-1）。

image

image

之后通过随机置换的方式，计算置换后数据的δ值（δ）。多次置换后，δ小于初始δ的概率即为p值。p值即代表了检验的显著性信息，p越低表明越容易接受观测δ值，MRPP结果越可信。

image

MRPP结果中通常会提供两种δ值：observed δ，即直接由公式计算的观测δ，值越小表明组内差异越小；以及expect δ，由置换过程得到的平均δ，值越大暗示了组间差异越大。

同时会结合observed δ和expect δ再计算一个简称为A值（chance-corrected within group agreement）的统计量。小于0表明组内差异大于组间差异，大于0表明组间差异大于组内差异。

image

关于方法的选择

对于具体选择哪种方法用于分析，考虑到在方法选择上本身就存在很多主观因素在里面，以下可以提供一些参考建议。

数据离散程度对各方法的影响

对于真实的数据集，PERMANOVA通常（但并非总是）比其它方法更强大。

总体而言，ANOSIM和Mantel test对离散程度比较敏感，二者中，ANOSIM通常比Mantel test更敏感。PERMANOVA在很大程度上不受均衡设计异质性的影响，也不受相关结构差异的影响。

对于非平衡的设计，上述所有的检验方法：当较小的组具有更大的异质性时过于宽松；当较大的组具有更大的异质性时过于保守，尤其是ANOSIM和Mantel test。也即表明，它们在不平衡设计中使用时需谨慎对待结果。

对于平衡设计，PERMANOVA可以在所选相似度量的范围内严格确定位置与分散效应；ANOSIM和Mantel test可以用作更多的“综合”测试，对组间位置、离散度或相关结构的差异敏感。

对于与排序分析相结合

如本篇开始提到的，这种基于距离的检验方法常和排序分析一起使用，很多文献中将它们与PCA、PCoA、NMDS等结合在一起，共同描述组间差异水平。

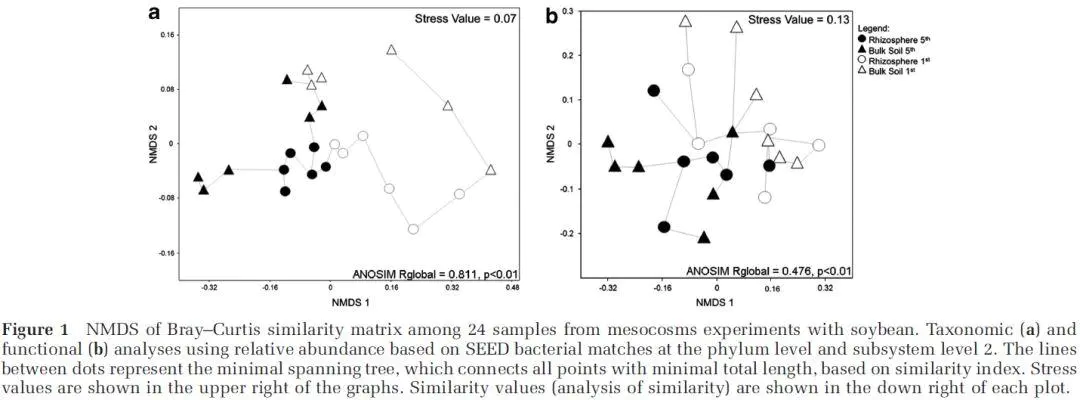
如下文献，显示了24个样品（2×2分组）的Bray-Curtis相异矩阵的NMDS分析，结合ANOSIM确定显著水平（Mendes et al, 2014）。

image

对于选择哪种差异检验方法与哪种排序方法结合，我看网上有教程说，由于ANOSIM是基于距离排名的方法，与NMDS配合更好；对于PERMANOVA，与PCoA配合更好。出现这些方法的文献中，也基本上这样搭配的。