文章首发于我的个人博客
1、FFT背景
快速傅里叶变换(FFT)是离散傅里叶变换(DFT)的快速算法,它是根据离散傅里叶的奇、偶、虚、实等特性,在DFT的基础上进行改进获得的。它对傅里叶变换的理论没有新的发现,但它的出现让离散傅里叶变换在计算机系统中得到了广泛的应用。
设x(n)为N项的复数序列,对其进行DFT,任一X(m)的计算都需要N次复数乘法和N-1次复数加法,因此要求出N项复序列的X(m),大约需要 N 2 N^2 N2次运算。当N逐渐增大时,运算量将呈指数式增长,这在实际应用中是一场灾难。而在FFT中,利用 W N W_N WN的周期性和对称性,把一个N项序列(设N=2k)分为两个N/2项的子序列,每个N/2点DFT变换需要 ( N 2 ) 2 (\frac{N}{2})^2 (2N)2次运算,再用N点运算把两个N/2点的DFT变换组合成一个N点的DFT变换。这样的变换总运算次数为 N + 2 ( N 2 ) 2 = N + N 2 2 N+2(\frac{N}{2})^2=N+\frac{N^2}{2} N+2(2N)2=N+2N2。如果将这种一分为二的思想一直继续下去,知道分成两两一组的DFT运算单元,那么N点的DFT变换就只需要Nlog2N次运算,当N为1024点时,运算量仅为10240次,是使用DFT算法的1%,点数越多,运算量的减少就越显著,这是FFT的优越性。
2、FFT推导
详细的推导在这里我不再重复,我推荐去看程佩青版本的《数字信号处理》基2DIT-FFT部分。
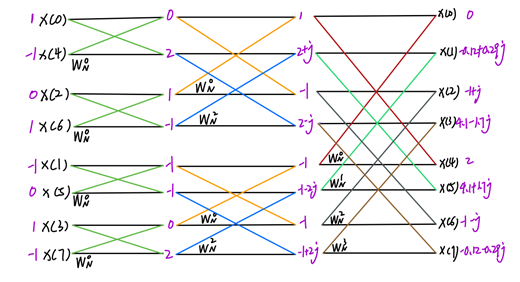
在此,我只通过一个8点DFT流图来说明FFT算法的核心原理,在我使用Python实现FFT代码的过程中,也是先实现上图所示的FFT流图,并不断地根据代码输出结果与正确结果之间的差别来DEBUG代码,不断完善,最终拓展到2048点的FFT。
实现基2DIT-FFT主要有三个步骤:
- 补零
- 抽取奇偶序列(倒序)
- 三个循环
- L级蝶形运算
- 2 L − m 2^{L-m} 2L−m个蝶形运算块
- 每个蝶形运算块中有 2 m − 1 2^{m-1} 2