文章概况
《Non-stationary Transformers:Exploring the Stationarity in Time Series Forecasting》是2022年发表于NeurIPS上的一篇文章。在过去的时序预测研究中,人们常通过数据平稳化减弱原始序列的非平稳性,这一做法与时序预测对突发事件预测的意义相悖,忽略了现实场景下非平稳数据的普遍存在性,最终导致建模和预测过平稳化。为了解决这个问题,该论文提出由序列平稳化和逆平稳化注意力组成的新的网络结构。
总体结构
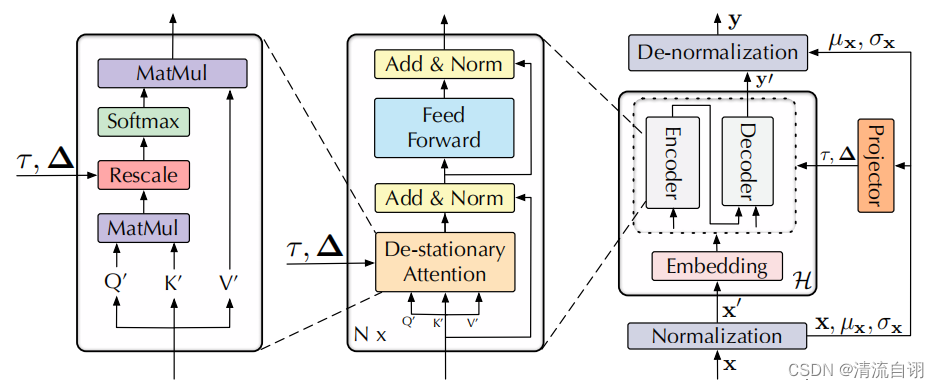
上图为本文所提模型结构。数据
x
x
x首先经过一个标准化模块(Normalization)获得变换后的序列
x
′
x^{'}
x′,接着对其进行编码操作,并将编码后的结果输入常见的Encoder-Decoder模块中,最终经过一个逆标准化模块(De-Normalization)后输出预测结果。其中一对标准化-逆标准化模块作者将其称为平稳化模块。与一般Transformer不同的是,作者对
Q
K
V
Q K V
QKV均作了调整,所提结构逆平稳化注意力模块(De-stationary Attention)代替了传统注意力模块,并接收了来自外界的两个参数
τ
τ
τ和
Δ
Δ
Δ用来计算注意力得分。
主要模块
Series Stationarization(序列平稳化模块)
非平稳化序列在预测任务中通常难度较大,因此人们希望将其转换为平稳数据进行预测。在此之前已有的方法:RevIN。该方法将输入数据进行标准化,并对标准化之后的结果添加可学习参数(权重a和偏置项b),最后在预测输出时进行对应的逆运算。该方法已被证实是有效的。受此启发,作者精简了RevIN的操作,舍弃了可学习参数,即数据的输入和输出只需要标准化和逆标准化。
De-stationary Attention(逆平稳化注意力模块)
序列平稳化模块确实能够有效将非平稳数据转化为平稳数据,但平稳化不可避免地丢失非平稳化特征,导致数据的过平稳化,这对时序预测的目的而言无疑是一场灾难。
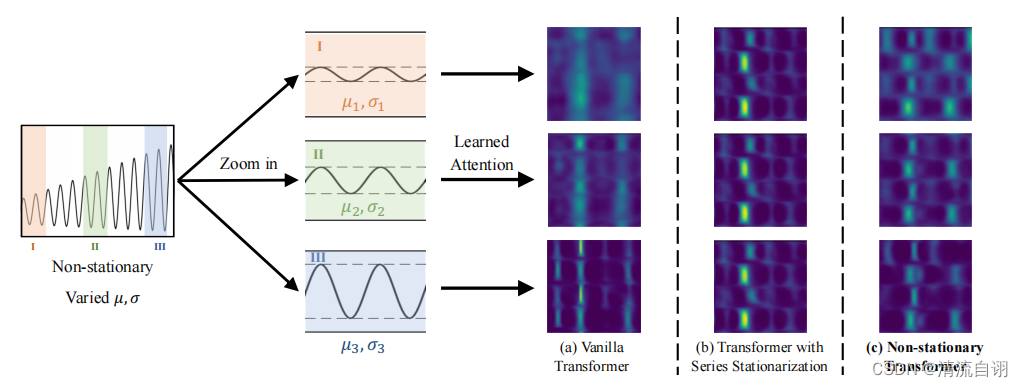
为了说明这一点,作者作出了注意力机制中所学习到的特征图,如上图所示。非平稳序列一般由若干个不同的子序列组成,将其中不同的子序列分别输入到一般性Transformer、带有序列平稳化模块的Transformer以及本文所提方法中。
可以发现,对不同子序列的特征提取,Transformer和本文方法提取到不同的三组特征,而带有序列平稳化模块的Transformer则提取到了非常相似的特征。这表明序列平稳化使得不同子序列提取的特征趋同,以丢失差异性特征的方法简化了特征提取的结果,不利于后续预测任务的开展。
与之形成对比的是本文所提方法,在序列平稳化后,成功地通过创新注意力模块来将原先丢失的非平稳化特征融入至注意力所学习到的特征中。接下来,我们来具体看看是如何做到的。
| 一般性注意力模块 | De-stationary Attention |
|---|---|
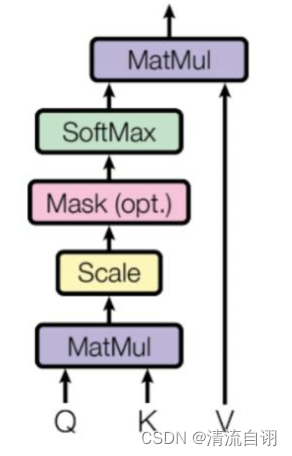 | 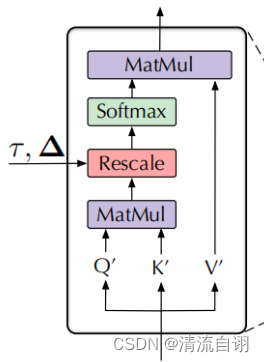 |
| z = s o f t m a x ( Q K T d k ) V z=softmax(\frac{QK^{T} }{\sqrt{d_{k} } } )V z=softmax(dkQKT)V | z ′ = s o f t m a x ( τ Q ′ K ′ T + 1 Δ T d k ) V ′ z'=softmax(\frac{τQ^{'}K^{'T} +1Δ^{T}}{\sqrt{d_{k} } } )V^{'} z′=softmax(dkτQ′K′T+1ΔT)V′ |
上面表格左边为一般性注意力模块,右边为文章所提De-stationary Attention。我们可以发现,两者的差别主要是后者调整了 Q K V Q K V QKV并多了 τ Δ τ Δ τΔ两个参数。通过这样的变化,作者尝试将非平稳特征添加进注意力模块中,具体计算步骤如下。
1.为了简化运算,假设
Q
Q
Q是由
x
x
x通过线性映射所得
2.为了便于公式的推导,假设每一批次的输入序列具有同样的期望和方差,
此时有
x
′
=
x
−
1
μ
x
T
σ
x^{'}=\frac{x-1\mu ^{T}_x}{\sigma }
x′=σx−1μxT,可得
Q
′
=
Q
−
1
μ
Q
T
σ
Q^{'}=\frac{Q-1\mu ^{T}_Q}{\sigma }
Q′=σQ−1μQT、
K
′
=
K
−
1
μ
K
T
σ
K^{'}=\frac{K-1\mu ^{T}_K}{\sigma }
K′=σK−1μKT
3.代入计算,可得
Q
′
K
′
=
1
σ
x
2
[
Q
K
T
−
1
(
μ
Q
T
K
T
)
−
(
Q
μ
K
)
1
T
+
1
(
μ
Q
T
μ
K
)
1
T
]
Q^{'}K^{'}=\frac{1}{\sigma^2_x}[QK^T-1(\mu^T_QK^T)-(Q\mu_K)1^T+1(\mu^T_Q\mu_K)1^T]
Q′K′=σx21[QKT−1(μQTKT)−(QμK)1T+1(μQTμK)1T]
4.因此可将原先的注意力公式转化为
s
o
f
t
m
a
x
(
Q
K
T
d
k
)
=
s
o
f
t
m
a
x
(
σ
x
2
Q
′
K
′
T
+
1
(
μ
Q
T
K
T
)
+
(
Q
μ
K
)
1
T
−
1
(
μ
Q
T
μ
K
)
1
T
d
k
)
softmax(\frac{QK^{T} }{\sqrt{d_{k} } })=softmax(\frac{\sigma^{2}_xQ'K'^T+1(\mu^T_QK^T)+(Q\mu_K)1^T-1(\mu^T_Q\mu_K)1^T}{\sqrt{d_{k}}})
softmax(dkQKT)=softmax(dkσx2Q′K′T+1(μQTKT)+(QμK)1T−1(μQTμK)1T)
5.此时第二点简化期望和方差为标量就发挥作用了。第四点的公式中分子上的最后两项为常数项,可以删去,这样便可得
z
′
=
s
o
f
t
m
a
x
(
Q
K
T
d
k
)
=
s
o
f
t
m
a
x
(
σ
x
2
Q
′
K
′
T
+
1
(
μ
Q
T
K
T
)
d
k
)
z'=softmax(\frac{QK^{T} }{\sqrt{d_{k} } })=softmax(\frac{\sigma^{2}_xQ'K'^T+1(\mu^T_QK^T)}{\sqrt{d_{k}}})
z′=softmax(dkQKT)=softmax(dkσx2Q′K′T+1(μQTKT))。
6.对于5中的公式,
Q
′
K
′
d
k
Q' K' \sqrt{d_{k}}
Q′K′dk已知(表格左图)可以计算得到,而与非平稳信号相关的
σ
x
\sigma_x
σx
K
K
K
μ
Q
\mu_Q
μQ,
σ
2
\sigma^2
σ2记为
τ
(
τ
≥
0
)
τ(τ≥0)
τ(τ≥0),
K
μ
Q
K\mu_Q
KμQ记为
Δ
Δ
Δ,作者使用多层感知机将其非平稳化特征带入到平稳化之后的计算中,可得
z
′
=
s
o
f
t
m
a
x
(
τ
Q
′
K
′
T
+
1
Δ
T
d
k
)
z'=softmax(\frac{τQ'K'^T+1Δ^T}{\sqrt{d_{k}}})
z′=softmax(dkτQ′K′T+1ΔT)。
l
o
g
τ
=
M
L
P
(
σ
x
,
x
)
和
Δ
=
M
L
P
(
μ
x
,
x
)
logτ=MLP(\sigma_x,x)和Δ=MLP(\mu_x,x)
logτ=MLP(σx,x)和Δ=MLP(μx,x)
实验结果
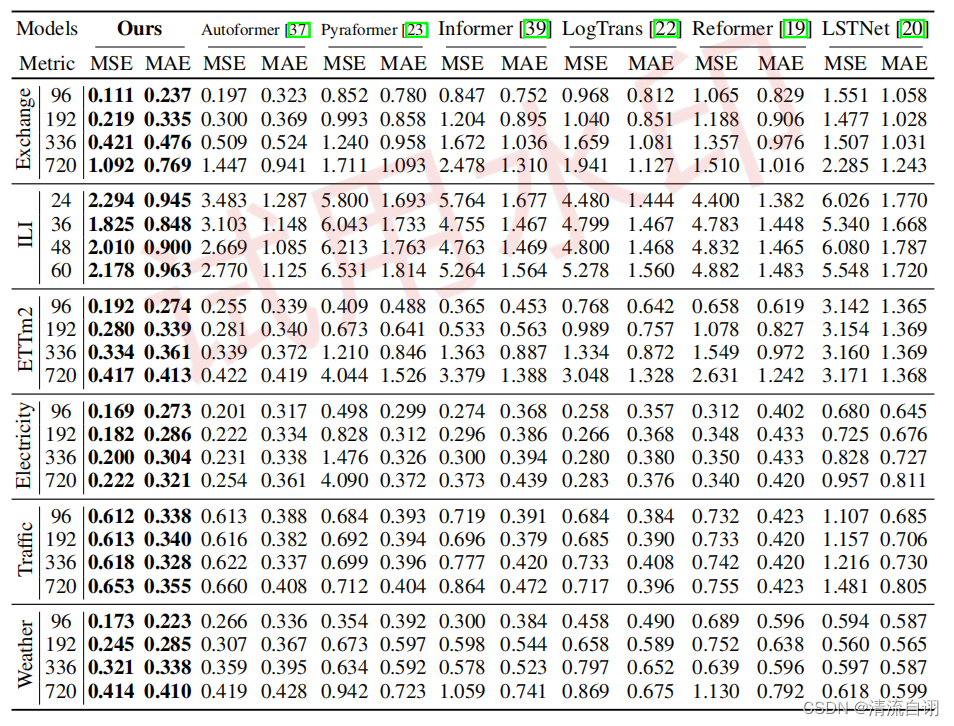
作者在真实世界中六种数据集进行测试,从实验角度和公式的推导角度说明了实验的先进性。
(更多实验结果见论文)
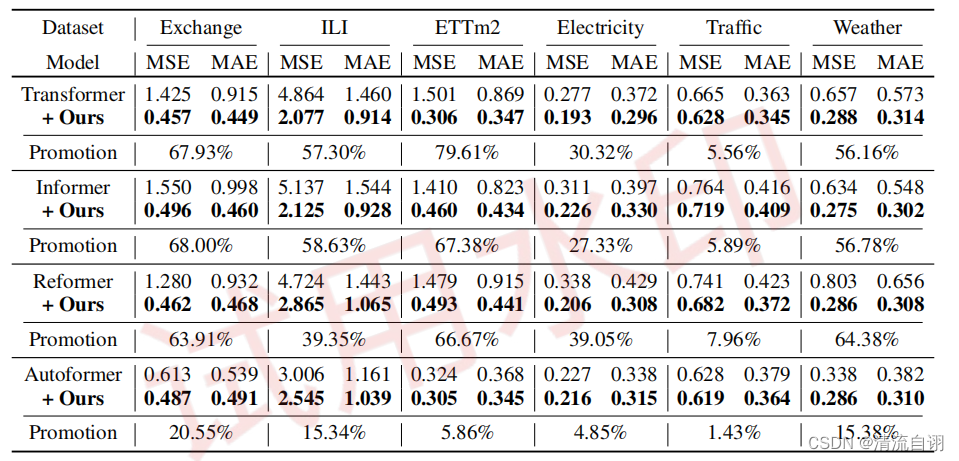
如上图,作者还将本文所提的框架应用于之前的Transformer模型中,通过实验说明了本文所提框架的优越性。
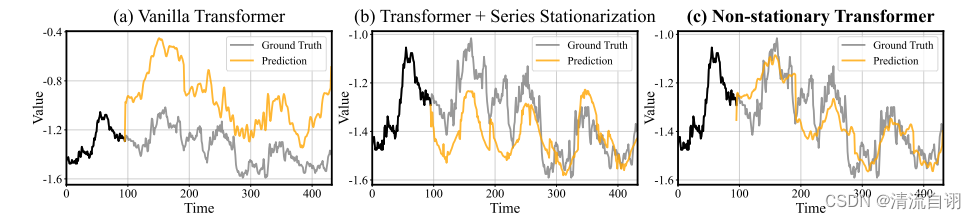
消融实验
该部分主要针对一般性Transformer、一般性Transformer+时序平稳以及本文所提方法进行对比。可以看出a、c具有显著的差异性波动,而b的波动相对稳定,显然是因为平稳化模块发挥的作用,而这正是作者所说的过平稳化。在逆平稳化注意力模块的帮助下,c中重回a中的非平稳状态,表现了该模块发挥的巨大的作用,一定程度减少了国过平稳化的负面影响,有利于时间序列准确的变化和预测,在这一类研究课题中具有重要的意义。
总结
这篇论文的目标很明确,指出过平稳化的问题并提出了一个有效的方法,这种方法在公式的推导中往往需要一些技巧,比如近似值处理、常数项归零、数学假设等等,虽然从纯理论的角度有些内容难以完美推导,但在各种化繁为简的操作下完成一套合理有效的试验方法其优异结果带来的价值已超出零散理论不足带来的弊病。