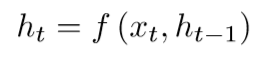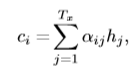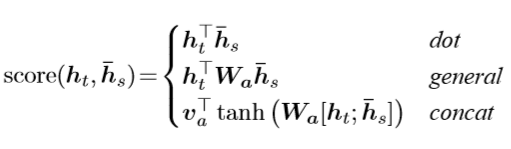前言
近日,阅读了两篇与attention机制相关的论文,为了防止看了就忘,写此文记录论文中一些要点,方便日后回顾,也为需要了解attention机制的朋友们提供一些参考。
两篇论文提出的attention机制都是基于机器翻译,实际上我们也可以应用于别处
论文地址
NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE
Effective Approaches to Attention-based Neural Machine Translation
Paper 1 :BahdanauAttention
基础介绍
当前机器翻译使用的神经网络模型普遍是seq2seq,基于encoder-decoder的思想。所谓encoder,就是将一个句子的信息压缩成一个向量 c c c,所谓decoder,就是利用这个向量 c c c来进行预测。Bahdanau在这篇论文中指出
In this paper, we conjecture that the use of a fixed-length vector is a bottleneck in improving the performance of this basic encoder–decoder architecture
将一个句子的所有信息都压缩成一个向量是提高机器翻译效果的瓶颈
所以Bahdanau提出了一种新的方式,即attention机制,他指出
In order to address this issue,we introduce an extension to the encoder–decoder model which learns to align and translate jointly. Each time the proposed model generates a word in a translation, it (soft-)searches for a set of positions in a source sentence where the most relevant information is concentrated. The model then predicts a target word based on the context vectors associated with these source positions and all the previous generated target words
也就是说,对原来的encoder-decoder模型进行扩展,可以让其在翻译的过程中,自动搜索一系列与源句子相关程度最大的位置,并且让模型聚焦这些位置。
这与传统encoder-decoder模型最大的不同就是,encoder部分不必再将一个很长的句子仅压缩成一个向量,而是每要翻译一个词的时候,将源句子编码成一个向量序列,然后对这些序列进行加权平均,求出当前待翻译词的上下文向量。
The most important distinguishing feature of this approach from the basic encoder–decoder is that it does not attempt to encode a whole input sentence into a single fixed-length vector. Instead, it encodes the input sentence into a sequence of vectors and chooses a subset of these vectors adaptively while decoding the translation. This frees a neural translation model from having to squash all the information of a source sentence, regardless of its length, into a fixed-length vector. We show this allows a model to cope better with long sentences.
seq2seq简介
上面说到的encoder-decoder 其实就是当下留下的seq2seq模型,即使用两个RNN循环神经网络,一个负责编码,一个负责解码。
对于encoder部分,我们可以把它抽象成一个函数,如下
这里的f描述的就是一个RNN,它接受两个输入,一个是源句子,一个是前一时刻的隐藏状态,输出的是当前时刻的隐藏状态。
对于decoder部分,也是一个RNN,我们可以把该网络抽象成一个函数,如下
y
=
g
(
y
t
−
1
,
s
t
,
c
)
y = g(y_{t-1},s_t,c)
y=g(yt−1,st,c)
也就是说该网络接受三个输入,分别是前一时刻的预测值
y
t
−
1
y_{t-1}
yt−1、当前时刻隐藏状态
s
t
s_t
st、上下文向量
c
c
c。
一般情况下,对于没有使用attention机制的seq2seq模型,这个上下文向量 c c c可能就是encoder部分的最后一个输出 h l h_l hl【这里 l l l表示源句子长度(单词数)】。
而如果我们引入了attention机制的话,那该机制的目标就是对于每一个待预测词都生成一个上下文向量 c c c
论文中的encoder部分
其论文中写的十分清楚,如下
Bahdanau在encoder的部分,使用的是双向循环神经网络其门控单元是GRU,那么对于每个时刻都会有两个隐藏状态输出,一个是前向的
h
→
h^{\rightarrow}
h→和后向的
h
←
h^{\leftarrow}
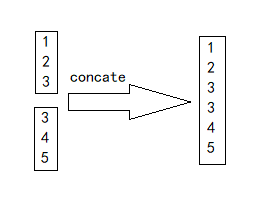
h←,Bahdanau的处理方法就是concate,也就是两个向量接在一起,图示如下。
现在对前向RNN中参数的维度进行说明
假设原来字典中有 K x K_x Kx个词,则 x t x_t xt的维度为 [ K x , 1 ] [K_x,1] [Kx,1]
假设词嵌入之后, x t x_t xt的维度变为 [ m , 1 ] [m,1] [m,1],那么其Embdding的矩阵维度为 [ m , K x ] [m,K_x] [m,Kx]
假设隐藏层中有n个隐藏单元,那么对于GRU各个门与 x x x相关的矩阵维度为 [ n , m ] [n,m] [n,m],那么与隐藏状态相关的参数的维度就是[n,n]
那么一个前向RNN某时刻输出的隐藏状态 h t h_t ht为[n,1],一个后向RNN某时刻输出的隐藏状态 h t h_t ht也为[n,1],两者进行concat,那么最终得到的每个时刻的隐藏状态维度就变为[2n,1]
这里为了更好的描述,所以忽略掉了偏置项,并不是说不需要偏置
论文中decoder的部分
Bahdanau在decoder的部分,使用一个单向的循环神经网络(门控单元为GRU)作为第一层,然后使用maxout layer作为第二层,即输出层。这里我们只关注第一层,第二层其实无所谓,你使用softmax也可以
先是对encoder部分生成的每一个隐藏状态序列
[
h
1
,
h
2
,
h
3
,
.
.
.
.
,
h
t
]
[h_1,h_2,h_3,....,h_t]
[h1,h2,h3,....,ht]进行加权求和,可以得到
c
i
c_i
ci。即
在这里我们先不关心
c
i
c_i
ci是如何而来,先来看看有了
c
i
c_i
ci,decoder的第一层是怎么进行输出的。
第一层的这个单向的RNN接收三个输入,分别是上一时刻预测的结果、上一时刻隐藏状态、上下文向量。所以三个输入各有一个参数矩阵,现在来看看分析以下其参数维度
这里有一个细节要注意,我们应该要通过词嵌入的方式对上一时刻预测结果进行其进行降维,即 E y i − 1 Ey_{i-1} Eyi−1
假设该单向RNN隐藏层单元数为 n ′ n' n′,翻译出来的语言其字典数大小为 K y K_y Ky,则 y i − 1 y_{i-1} yi−1的维度为[ K y K_y Ky,1]
进行词嵌入降为之后其维度变为[d,1],那么Embedding的参数E的维度就为[d, K y K_y Ky]
因为 c i c_i ci是 h t h_t ht的加权求和,所以其维度是[2n,1]
那么对于GRU门控单元来说,与上一时刻输入相关的参数W,其维度[
n
′
n'
n′,d]
那么对于GRU门控单元来说,与上一时刻隐藏层状态相关的参数U,其维度[
n
′
n'
n′,
n
′
n'
n′]
那么对于GRU门控单元来说,与上下文向量相关的参数C,其维度[
n
′
n'
n′,2n]
其输出状态 s t s_t st维度为[ n ′ n' n′,1]
论文中attention部分
上面说到,我们需要对encoder输出的各个时刻的隐藏状态进行加权求和,那么关键是这个权重该怎么求?
其实非常简单,在原论文中是这样的描述的
总结一下就是如下形式
α
i
j
=
s
o
f
t
m
a
x
(
v
a
T
t
a
n
h
(
W
a
s
i
−
1
+
U
a
h
j
)
)
\large \alpha_{ij} = softmax(v_a^{T}tanh(W_as_{i-1} + U_ah_j))
αij=softmax(vaTtanh(Wasi−1+Uahj))
如果我们令
a
(
s
i
−
1
,
h
j
)
=
v
a
T
t
a
n
h
(
W
a
s
i
−
1
+
U
a
h
j
)
a(s_{i-1},h_j) = v_a^{T}tanh(W_as_{i-1} + U_ah_j)
a(si−1,hj)=vaTtanh(Wasi−1+Uahj)
那么
α
i
=
s
o
f
t
m
a
x
(
a
(
s
i
−
1
,
h
1
)
,
a
(
s
i
−
1
,
h
2
)
,
.
.
.
a
(
s
i
−
1
,
h
l
)
)
\large \alpha_{i} = softmax(a(s_{i-1},h_1),a(s_{i-1},h_2),...a(s_{i-1},h_l))
αi=softmax(a(si−1,h1),a(si−1,h2),...a(si−1,hl))
那么实际上所谓attention机制就是一个前馈神经网络和一个softmax函数的组合,这个前馈神经网络接受一个向量[s,h],所以其输入层维度为[
n
′
n'
n′+2n,1],隐藏层有
n
′
n'
n′个单元,激活函数为tanh,输出层只有一个单元,没有激活函数
在计算 α i \alpha_{i} αi的时候,就把 [ s t − 1 , h 1 ] 、 [ s t − 1 , h 2 ] 、 [ s t − 1 , h 3 ] 、 [ s t − 1 , h 4 ] . . . . . . [ s t − 1 , h l ] [s_{t-1},h_1]、[s_{t-1},h_2]、[s_{t-1},h_3]、[s_{t-1},h_4]......[s_{t-1},h_l] [st−1,h1]、[st−1,h2]、[st−1,h3]、[st−1,h4]......[st−1,hl](这里的l为encoder隐藏状态的个数)送入这个前馈神经网络a进行计算,最后就会得到 l l l个值,然后再将这 l l l个值送入softmax函数,就可以得到一个加权平均值了
现在来分析一下参数维度,计算 α i j \alpha_{ij} αij需要用到两处的信息 ,分别是decoder中前一时刻的隐藏状态 s t − 1 s_{t-1} st−1、encoder中的所有隐藏状态 h h h。
s t − 1 s_{t-1} st−1维度为[ n ′ n' n′,1],所以 w a w_a wa的维度为[ n ′ n' n′, n ′ n' n′],所以 s t − 1 w a s_{t-1}w_a st−1wa
h h h的维度为[2n,1],所谓 U a U_a Ua的维度为[ n ′ n' n′,2n]
我们发现计算完
W
a
s
i
−
1
+
U
a
h
j
W_as_{i-1} + U_ah_j
Wasi−1+Uahj,其维度固定成[
n
′
n'
n′,1],所以我们也称其为对齐
为了将对其后的向量转换成一个标量,所以 v a v_a va的维度为[n,1],那么转置之后其维度就变成 [ 1 , n ] [1,n] [1,n]
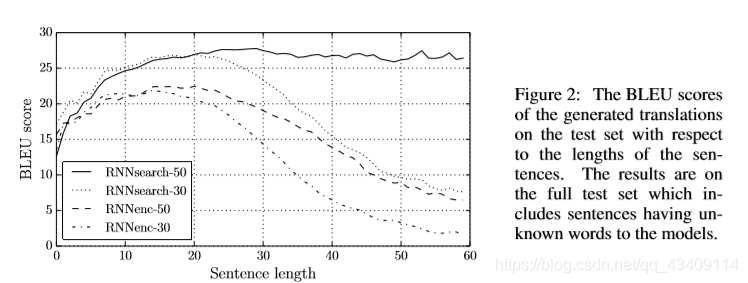
BahdanauAttention的实验结果
RNNsearch-50、RNNsearch-30分别是指使用attention机制,训练语句的单词数目长度不超过50、使用attention机制,训练语句的单词数目长度不超过30
RNNenc-50、RNNenc-30分别是指不使用attention机制,训练语句的单词数目长度不超过50、不使用attention机制,训练语句的单词数目长度不超过30
可以看到,使用了attention机制的模型,哪怕句子变得很长,也可以维持较高水平的翻译效果
Paper 2:LuongAttention
基础介绍
Luong 基于BahdanauAttention提出了两种新的注意力机制:global attention、local attention。论文描述如下
In this work, we design, with simplicity and effectiveness in mind, two novel types of attentionbased models: a global approach in which all source words are attended and a local one whereby only a subset of source words are considered at a time. The former approach resembles the model of (Bahdanau et al., 2015) but is simpler architecturally
local attention 比global attention更容易训练,且时间复杂度更低,除此之外Luong提出了多种对齐方式
it is computationally less expensive than the global model or the soft attention; at the same time, unlike the hard attention, the local attention is differentiable almost everywhere, making it easier to implement and train.2 Besides, we also examine various alignment functions for our attention-based models.
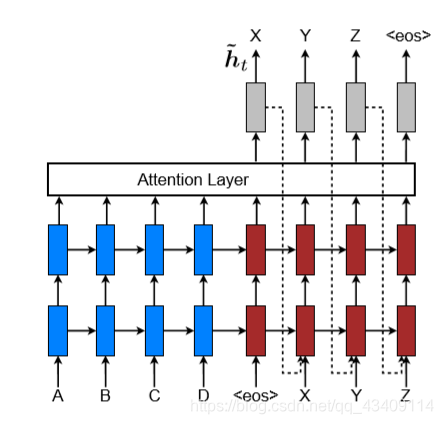
Luong在encoder-decoder模型中使用的是两层单向循环神经网络且门控单元为LSTM,模型图如下。
观察上图我们可以发现,encoder的最后时刻的隐藏状态
h
t
h_t
ht没有进行任何转换,直接送入到了decoder中,所以encoder和decoder中的隐藏神经元数目是一样的,我们暂且设置为
n
n
n,这也是Bahdanau和Luong提出的attention机制的区别之一。
Attention-based Models
Luong首先定义了模型的基础部分,为什么要定义这个基础部分呢?因为
g
l
o
b
a
l
a
t
t
e
n
t
i
o
n
global attention
globalattention和
l
o
c
a
l
a
t
t
e
n
t
i
o
n
local attention
localattention只有计算权重时候是不一样的,其他部分都是相同的,同理,我们计算出了权重就可以使用这一基础模型进行运算啦。
注意,这个模型中的RNN网络是双层的,所以每一层都会有隐藏状态,这里我们只取第二层的隐藏状态,不考虑第一层的隐藏状态。
这个基础模型定义了,我们在拥有上下文向量 c t c_t ct和当前时刻的decoder的隐藏状态 h t h_t ht时,我们该如何计算预测值(概率值)
实际上就是两步骤,第一步根据上图中公式(5)来算计算 h h h,然后对 h h h进行softmax。
另外需要注意的是,在这里我们对上下文向量 c t c_t ct和decoder的隐藏状态 h t h_t ht进行了concate操作,然后将concat的结果进行仿射变换之后输入到softmax中计算概率分布。而在BahdanauAttention中,我们将 c t c_t ct用在了计算 s t s_t st上,然后直接将 s t s_t st输入到softmax中计算概率分布
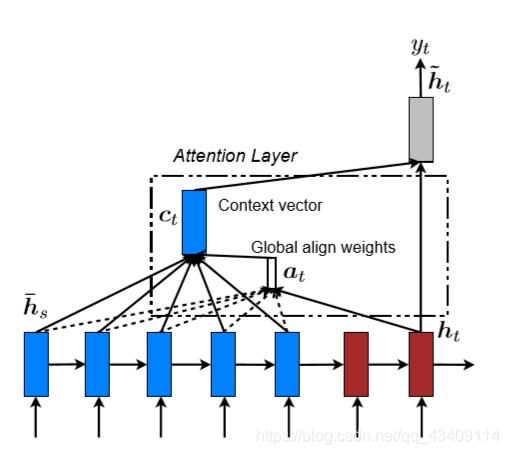
global attention 部分
由基础模型可知,要想得到结果一定要先把上下文向量 c t c_t ct求出来。
global attention的算法就是来求
c
t
c_t
ct的,其思想与BahdanauAttention几乎一摸一样,都是对encoder的隐藏状态进行加权平均,算法目标都是为了计算权重大小,他们俩之间的区别就在于权重大小的计算方式不一样 或者说对齐方式不一样,在Bahdanau中只提出了一种对齐方式,而Luong提出了三种对齐方式
,Luong给出的权重值计算公式如下
上面的score就是对齐函数,可以从三个中任选一个,描述如下。
现在我们来分析一下,三种表达式中的维度信息
dot、general、concat中 h s ˉ \bar{h_{s}} hsˉ维度[n,1]、 h t h_{t} ht维度[n,1]、
general中的 W a W_a Wa的维度[n,n]、
concat中的 W a W_a Wa的维度[m,2n], v a v_a va的维度[1,m]
总之:score函数的输出是一个标量
那么global attention计算权重 α \alpha α的方法大概可以总结如下:
- 分别计算 [ h t , h 1 ˉ ] [h_t,\bar{h_1}] [ht,h1ˉ]、 [ h t , h 2 ˉ ] [h_t,\bar{h_2}] [ht,h2ˉ]、 [ h t , h 3 ˉ ] [h_t,\bar{h_3}] [ht,h3ˉ]… [ h t , h s ˉ ] [h_t,\bar{h_s}] [ht,hsˉ]的score值,得到一个向量 [ s c o r e 1 , s c o r e 2 , s c o r e 3 , . . . , s c o r e s ] [score_1,score_2,score_3,...,score_s] [score1,score2,score3,...,scores]
- 然后将该向量送入softmax函数即可得到s个权重
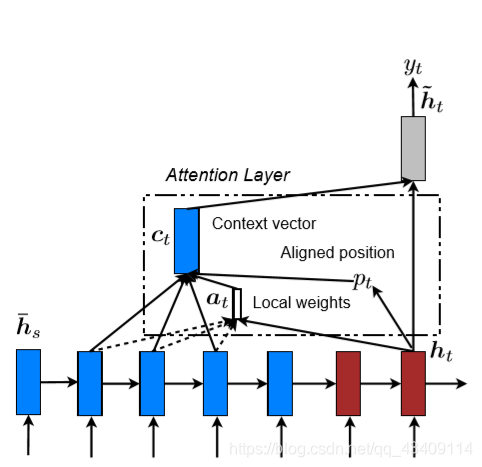
local attention部分
先看看local attention和global attention的模型图
我们可以一眼就看出区别,global attention考虑 encode隐藏状态的时候是全部考虑,而local attention考虑隐藏状态的时候是只考虑一部分。
论文作者是这样评价global attention的
The global attention has a drawback that it has to attend to all words on the source side for each target word, which is expensive and can potentially render it impractical to translate longer sequences, e.g., paragraphs or documents. To address this deficiency, we propose a local attentional mechanism that chooses to focus only on a small subset of the source positions per target word.
大概意思就是,global attention有个缺点,在预测很长的句子的时候,其预测结果可能会不符合文意,也就是跑题。所以为了解决这个问题又提出local attention,该attention机制每次会将注意力放在原始数据的一小部分上,而不是统统考虑。至于每次应该将注意力放在哪里,这是靠模型学习得来的。
下面的段落就是关于模型怎么选择应该将注意力放在哪里
下面解释一下上述论文锻炼大意
假设我们的encoder中隐藏状态一个有 l l l个
那么我们的local attention模型会生成一个整数值 p t p_t pt,该值的大小在 [ 0 , l ] [0,l] [0,l]之间,
D是一个我们事先设置好的经验值, 有了 p t 、 D p_t、D pt、D就可以计算出模型应该关注的窗口范围 [ p t − D , p t + D ] [p_t-D,p_t+D] [pt−D,pt+D]
也就是说D决定了注意力窗口的大小,其窗口大小为 2 × D + 1 2\times D+1 2×D+1
然后我们计算encoder中位置在 [ p t − D , p t + D ] [p_t-D,p_t+D] [pt−D,pt+D]中的隐藏状态的加权平均值,即可得到 上 下 文 向 量 c t 上下文向量c_t 上下文向量ct
Luong又提出了
p
t
p_t
pt的两种生成方式,所以local attention又可以分为local m、local p
上述段落解释的很清楚了,我就不再赘述了。
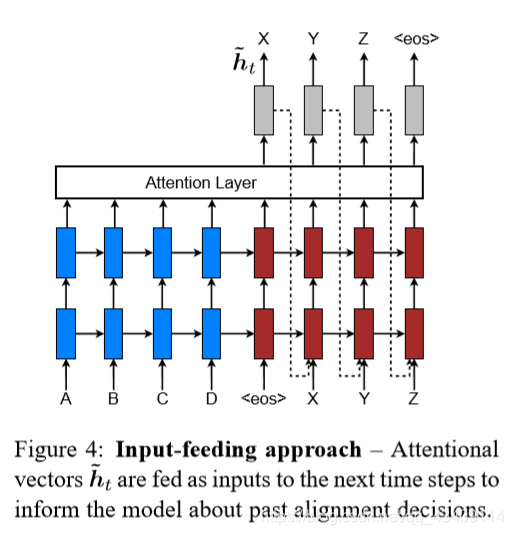
Input-feeding Approach
Luong还提出了Input-feeding Approach这个方法,这个方法是为了让模型能够关注那些已经被翻译了的单词,其做法就是将decoder前一个
h
~
\widetilde{h}
h
与前一个decoder的预测结果拼接在一起,作为下一个时刻的输入
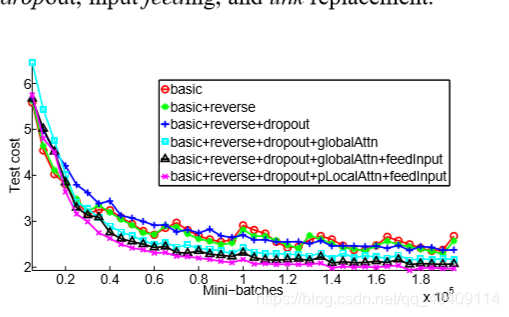
实验结果
上图basic指的是没有用任何优化方法的seq2seq模型,我们可以看到local-p在测试集上的是效果最好的
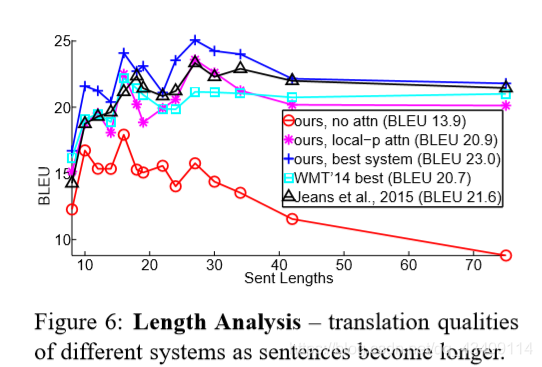
上图刻画了当待翻译单词数逐渐增大时,模型的预测结果走势情况。可以看到采样了attention机制的模型普遍要好一些
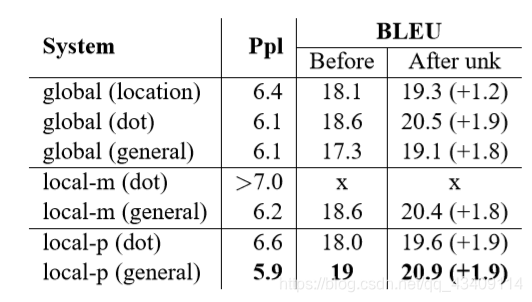
上面这幅图就刻画了,三种score函数、local-p、local-m、global进行部分组合使用时,模型的效果,作者在论文说到score函数的concata效果不太好,所以就不没又列出来。所以总结一下,推荐使用local-p + general的组合。