Cuda GEMM优化
内存大小:global memory > L2 cache > L1/SMEM > Register
带宽大小:Register > L1/SMEM > L2 cache > global memory
1. Naive GEMM
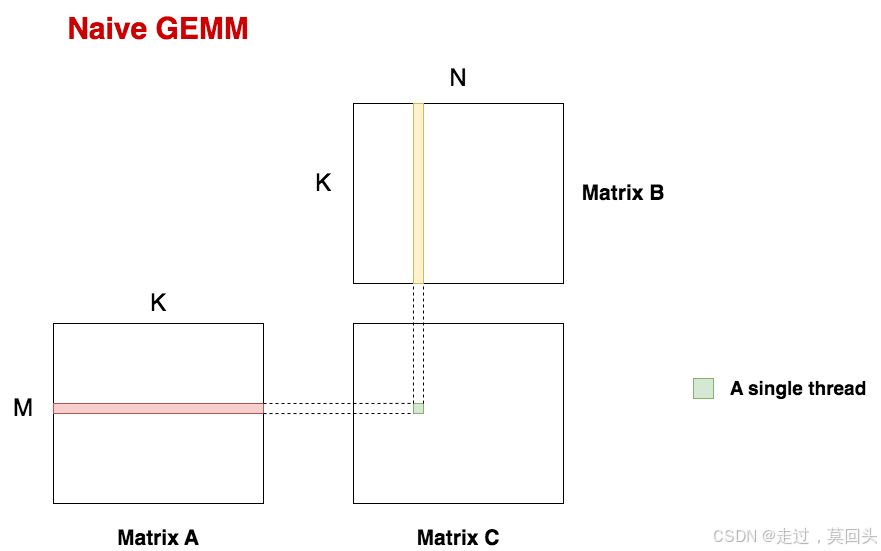
每个thread负责读取A矩阵的一行和B矩阵的一列,去计算C矩阵的一个元素。则一共需要M*N个thread。
矩阵A和矩阵B都存储在global memory,每个thread直接从global memory上进行读数,完成计算:
-
为了计算出C中的某个元素,每个thread每次都需要从global memory上读取A矩阵的一行(K个元素),B矩阵的一列(K个元素),则每个thread从global memory上的读取次数为2K。
-
C中共有M*N个thread,则为了计算出C,对global memory的总读取次数为2KMN:。
这里及之后的分析中,我们不考虑把结果矩阵C写回global memory需要的次数,只考虑“读”。
可想而知,由于这种办法要重复从global memory上读取数据,所以读取数据上消耗了大量时间,它肯定没有办法充足利用起GPU的算力。
2. GEMM优化:矩阵分块,从global memory到SMEM
我们知道on-chip内存的带宽要比off-chip内存的带宽大得多。所以如果我把矩阵A和B都搬运到on-chip的SMEM上,然后采用和naive GEMM一样的计算方法,那么尽管还是会在SMEM上发生重复读数据的情况(也即总的读写次数和naive一样,只不过现在不是从global memory读取,是从SMEM上读取),可是因为带宽变大了,总体来说数据读取时间肯定减少了。
但是问题是,SMEM的存储要比global memory小很多,当矩阵比较大时,根本没办法把完整的矩阵搬运到SMEM上。那该怎么办呢?
很简单,如果搬运不了完整的矩阵,那我对矩阵切切块,搬运它的一部分,不就行了吗?
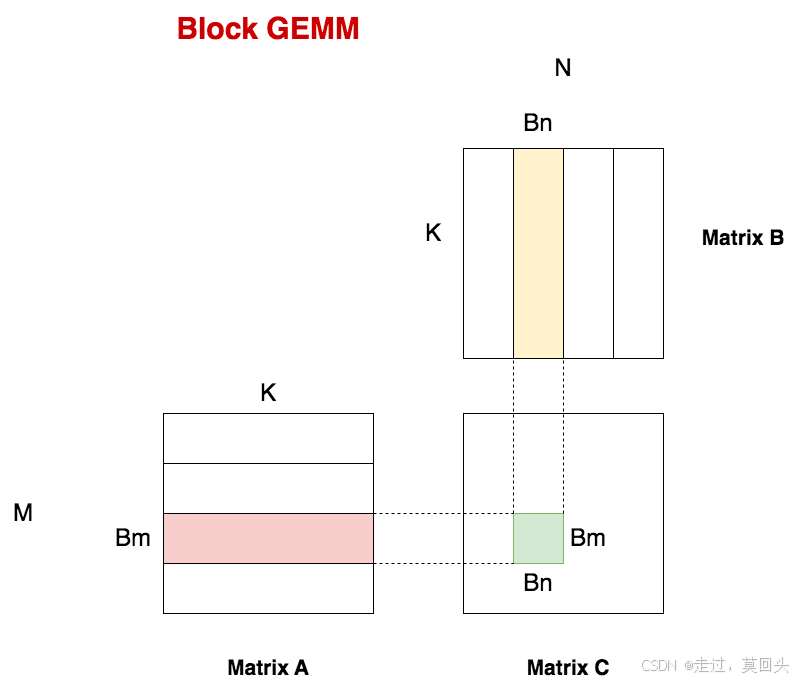
如图:
- 把A矩阵横着切分成四块,每块大小为 ( B m , B k ) = ( 128.512 ) (B_m,B_k)=(128.512) (Bm,Bk)=(128.512)
- 把B矩阵纵着切分成四块,每块大小为 ( K , B n ) = ( 512 , 128 ) (K,B_n)=(512,128) (K,Bn)=(512,128)。
A和B对应的切块(如图中的红色和黄色块)组成一个cuda编程里的block,这里我们共有4*4 = 16个block,每个block负责计算C矩阵中大小为的部分(图中绿色块)。易知每个block间的计算是独立的。
好!那么现在我只需要把A的分块(红色)与B的分块(黄色)从global memory搬运到SMEM上,然后再从SMEM做一系列读取操作去计算C。如此循环,直到所有的C分块都计算出来为止。这不就能帮我省一笔读取数据的时间么?
这个策略虽然可行,但现在我们再上点难度:如果SMEM还是装不下
(
B
m
,
K
)
(B_m,K)
(Bm,K),
(
K
,
B
n
)
(K,B_n)
(K,Bn)
大小的切块,那要怎么办?
那就再继续切呗:
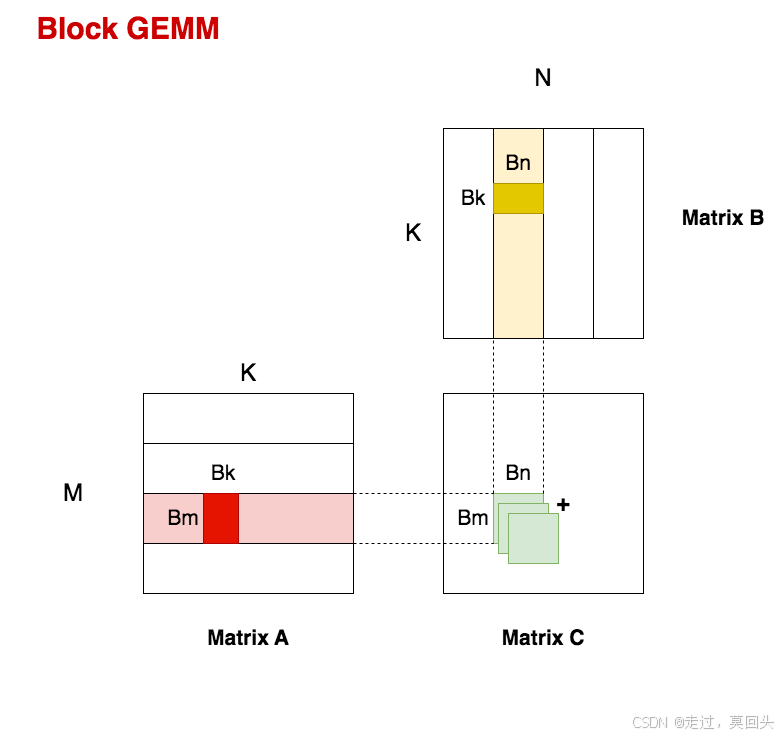
上图中A矩阵的高亮红块,B矩阵中的高亮黄块,就是我们再切割的结果:
- A矩阵中的 ( B m , B k ) (B_m,B_k) (Bm,Bk),一般我们取 B k = 8 B_k = 8 Bk=8,因此最终A切块的大小为 ( 128 , 8 ) (128,8) (128,8)
- B矩阵中的 ( B k , b n ) (B_k,b_n) (Bk,bn),最终B切块的大小为 ( 8 , 128 ) (8,128) (8,128)
按照现在的划分,我们现在理一下一个block内做的事情:
- 每次取A矩阵的一个分块 ( B m , B k ) (B_m,B_k) (Bm,Bk),取B矩阵的一个分块 ( B k , B n ) (B_k,B_n) (Bk,Bn),将两者相乘得到分块矩阵 C C C
- 对 A A A矩阵,向右找到下一个分块;对 B B B矩阵,向下找到下一个分块,然后再相乘得到分块矩阵 C C C,累加到上一个分块矩阵 C C C上。
- 如此循环,当我们遍历完所有的A分块和 B B B分块后,就可以得到最终的分块矩阵 C C C了。也就是我们图中的高亮绿块 ( B m , B n ) (B_m,B_n) (Bm,Bn)。
现在我们来计算下切块方式下对global memory的读取次数:
- 对于图中一块尺寸为 ( B m , B n ) (B_m,B_n) (Bm,Bn)矩阵分块 C C C,每次都要从global memory读取大小为 ( B m , B k ) (B_m,B_k) (Bm,Bk)矩阵分块 A A A和大小为 ( B k , b n ) (B_k,b_n) (Bk,bn)矩阵分块 B B B,对global memory的读取次数为 B m B k + B k B n B_mB_k+B_kB_n BmBk+BkBn。每个block内这样的操作一共要经历 K B k \cfrac{K}{B_k} BkK次。最终每个block在global memory的读取次数为: K B k ( B m B k + B k B n ) = K ( B m + B n ) \cfrac{K}{B_k}(B_mB_k+B_kB_n)=K(B_m+B_n) BkK(BmBk+BkBn)=K(Bm+Bn)
- block的数量为 M B m ∗ N B n \cfrac{M}{B_m} * \cfrac{N}{B_n} BmM∗BnN
- 综上两点,切块方式下对global memory最终的读取次数为: M B m ∗ N B n ∗ K ( B m + B n ) = M N K ( 1 B m + 1 B n ) \cfrac{M}{B_m} * \cfrac{N}{B_n} * K(B_m+B_n)=MNK(\cfrac{1}{B_m} + \cfrac{1}{B_n}) BmM∗BnN∗K(Bm+Bn)=MNK(Bm1+Bn1)
所以现在我们有:
- 不分块情况(naive gemm)下对global memory的读取次数: 2 M N K 2MNK 2MNK
- 分块情况下对global memory的读取次数: M N K ( 1 B m + 1 B n ) MNK(\cfrac{1}{B_m} + \cfrac{1}{B_n}) MNK(Bm1+Bn1)
由此可知 B m , B n B_m, B_n Bm,Bn越大时,分块情况下对global memory的读写次数越少,使得gpu相对花更多的时间在计算而不是在读数上,更有效利用gpu。但是受到SMEM大小的限制, B m , B n B_m, B_n Bm,Bn也不宜过大,不然一次加载不了那么多数据。