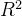多项式回归（Polynomial Regression）

多项式回归（Polynomial Regression）的理论知识推导

多项式回归是一种回归分析方法，其中自变量的关系通过多项式方程建模，而不是线性方程。多项式回归可以用于建模非线性数据，特别是当数据呈现出弯曲或非线性趋势时。

1. 数学模型

多项式回归的模型假设因变量 yyy 和自变量 xxx 之间的关系可以表示为：

2. 目标函数

3. 参数解读

实施步骤

数据准备：
- 收集数据。
- 将数据分为训练集和测试集。
数据预处理：
- 处理缺失值。
- 数据标准化或归一化（视情况而定）。
多项式特征生成：
- 生成高次项特征。
建立模型：
- 使用训练数据拟合多项式回归模型。
模型评估：
- 使用测试数据评估模型性能。
- 计算 R2R^2R2、均方误差（MSE）等指标。
预测：
- 使用训练好的模型进行预测。

多项式回归的Python实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# 生成示例数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + X**2 + np.random.randn(100, 1) * 0.5

# 数据分割为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 生成多项式特征
poly = PolynomialFeatures(degree=2)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

# 创建线性回归模型
lin_reg = LinearRegression()
lin_reg.fit(X_poly_train, y_train)

# 进行预测
y_poly_pred = lin_reg.predict(X_poly_test)

# 模型评估
mse = mean_squared_error(y_test, y_poly_pred)
r2 = r2_score(y_test, y_poly_pred)

print(f"Mean Squared Error: {mse}")
print(f"R^2 Score: {r2}")
print(f"Intercept: {lin_reg.intercept_}")
print(f"Coefficients: {lin_reg.coef_}")

# 可视化结果
plt.scatter(X_test, y_test, color='blue', label='Actual')
plt.scatter(X_test, y_poly_pred, color='red', label='Predicted')
plt.xlabel("X")
plt.ylabel("y")
plt.title("Polynomial Regression")
plt.legend()
plt.show()

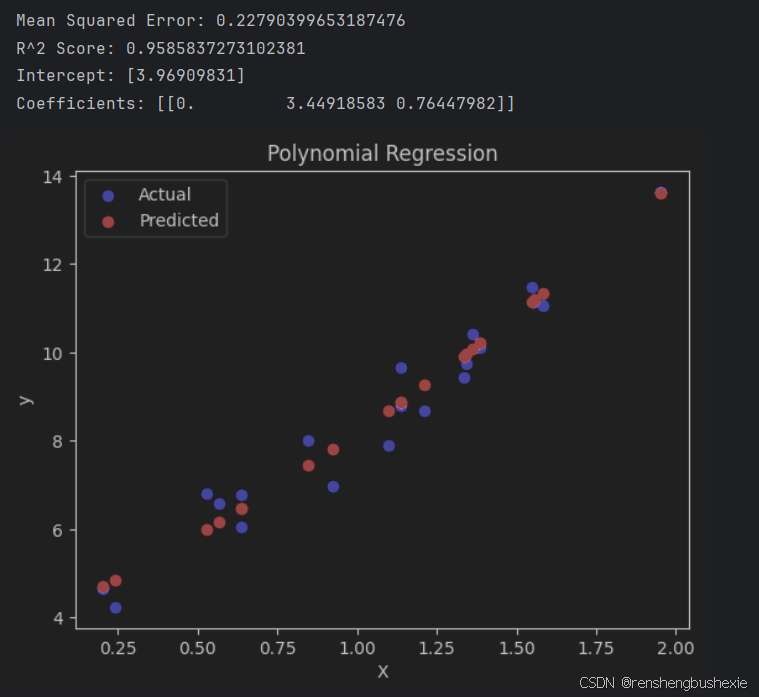
可视化展示

结果与解释

Mean Squared Error (MSE): 衡量预测值与实际值之间的平均平方误差。值越小，模型性能越好。
$R^{2}$ Score: 决定系数，度量模型的拟合优度，范围从0到1，值越接近1，模型解释力越强。
Intercept: 截距，即回归方程在y轴上的截距。
Coefficients: 回归系数，表示自变量对因变量的影响。

在可视化结果中，蓝色点表示测试集的实际数据，红色点表示多项式回归模型的预测结果。通过这些结果，可以观察到多项式回归如何更好地拟合非线性数据趋势。

通过上述实例，可以看到多项式回归模型如何在数据中找到最佳拟合曲线，并且通过MSE和 $R^{2}$ 等指标评估模型性能。