数组值随机

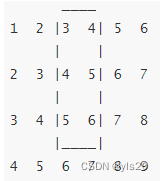
1  2  3  4  5  6
      ____
2  3 |4  5| 6  7
     |    |
3  4 |5  6| 7  8
     |____|
4  5  6  7  8  9


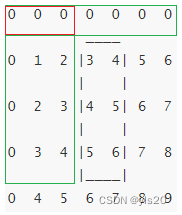
//sums 回头看，第一遍忽略。添加 0 边界，充当缓冲区
0  0  0  0  0  0  0
         ____
0  1  2 |3  4| 5  6
        |    |
0  2  3 |4  5| 6  7
        |    |
0  3  4 |5  6| 7  8
        |____|
0  4  5  6  7  8  9

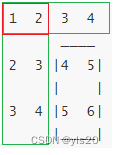
求左上角坐标（1，2）到右下角坐标（2，3）的子矩阵的和

首先，两个问题：

（1）如何得到子矩阵的值

（2）如何计算每一个点前缀和

解决第一个问题：

定义二维数组 sums[i][j] 表示，从左上角坐标（0，0）到右下角坐标（i，j）矩阵的和

如何得到左上角坐标（1，2）到右下角坐标（2，3）的子矩阵的和？

抽象一下：

sums[2][3] ——

sums[2][1] ——

sums[0][3] ——

可以看到重复删了 [1,2] ，因此加上 sums[0][1] ——

因此左上角坐标（1，2）到右下角坐标（2，3）的子矩阵的和 = sums[2][3] - sums[2][1] -sums[0][3] + sums[0][1]

化为公式：

左上角坐标（i1，j1）到右下角坐标（i2，j2）的子矩阵的和 = sums[i2][j2] - sums[i2][j1 - 1] - sums[i1 - 1][j2] + sums[i1 - 1][j1 - 1]

解决第二个问题：

以 sums[2][3] 表示：

初始化是一个遍历过程，因此假设 sums[2][3] 前的元素已经初始化完成

很简单，两部分构成 sums[2][3] = sums[1][3] + 当前行的 sum[3]

外循环是行，内循环是列

抽象一下：sums[i][j] = sums[i - 1][j] + 当前行的 sum[j]

细节值得注意： sums[0][3] ——

当左上角坐标是 （1，2）时，减去的一部分坐标为 sums[0][3]，也就是索引 i 到 0 了

如果左上角坐标是 （0，2）时呢？

这一部分坐标将是 （-1，3）了，以此为了索引不越界问题，sums[i+1][j+1] 数组定义表示，从左上角坐标（0，0）到右下角坐标（i，j）矩阵的和

所以公式也将发生变化：

左上角坐标（i1，j1）到右下角坐标（i2，j2）的子矩阵的和 = sums[i2 + 1][j2 + 1] - sums[i2 + 1][j1] - sums[i1][j2 + 1] + sums[i1][j1]

（0，0）到（i，j）的矩阵和 sums[i + 1][j + 1] = sums[i][j + 1] + 当前行的 sum[j + 1]

import java.util.*;

public class Test{
    public static void main(String[] args) {
        int[][] arr = {
                {1,2,3,4,5},
                {2,3,4,5,6},
                {3,4,5,6,7},
                {4,5,6,7,8},
                {5,6,7,8,9}
        };

        System.out.println(subMatrixSum(arr,1,2,3,4));
    }

    private static int subMatrixSum(int[][] arr,int row1,int col1,int row2,int col2) {
        int[][] sums = new int[arr.length + 1][arr[0].length + 1];
        for(int i = 0; i < arr.length; i++) {
            int rowSum = 0;
            for(int j = 0; j < arr[0].length; j++) {
                rowSum += arr[i][j];
                sums[i+1][j+1] = sums[i][j+1] + rowSum;
            }
        }

        return subMatrixSumCore(sums,row1,col1,row2,col2);
    }

    private static int subMatrixSumCore(int[][] sums,int row1,int col1,int row2,int col2) {
        return sums[row2+1][col2+1] - sums[row1][col2+1] - sums[row2+1][col1] + sums[row1][col1];
    }
}

54