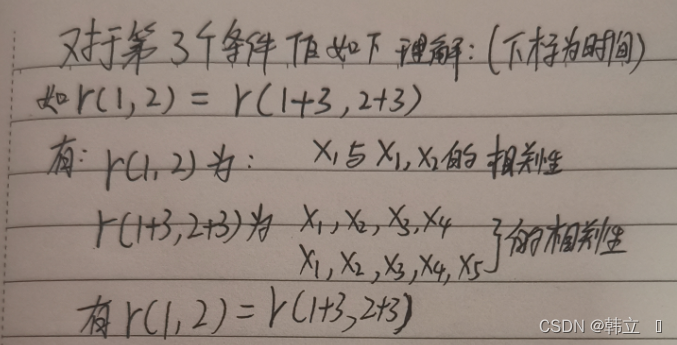目录
总结精华(讲了这么多的目的和最终怎么用):总之,我们拿到一个时间序列,我们要做两个检验:
时间序列分类:
1:时间序列分为平稳时间序列和非平稳时间序列。其中平稳时间序列又分为严平稳时间序列和宽平稳时间序列。下面主要讲解平稳序列,在讲解之前我们先引入概率分布的意义。
1.1:概率分布的意义:
时间序列的联合分布定义为:
举例理解:
但是实际应用中我们都是通过样本估计总体,所以研究样本的统计量非常必要:
1.2:统计量的定义:
注:从样本角度理解如下(有助于我们理解总体):
注:从样本角度理解如下:
2:有了上面的概念后我们开始定义平稳序列:
2.1:更具体的说,我们一般研究宽平稳序列,宽平稳序列定义如下:
2.2:两种平稳序列的关系:
2.3:宽平稳序列性质(也就是定义):
对于宽平稳序列,我们有如下说明定义(该定义并不增加新概念):
3:从样本角度,对以上概念再次描述定义:
平稳时间序列的检验:
我们获取了时间序列的概念和定义,很自然的我们想知道如何判定一个时间序列是否是时间序列呢? 所以,自然引出时间序列的检验问题。
1:图检验方法:
2:时序图检验方法原理(从定义中获取的检验方法):
注:其实就是检验观察值均值序列是否一直是同一个值。
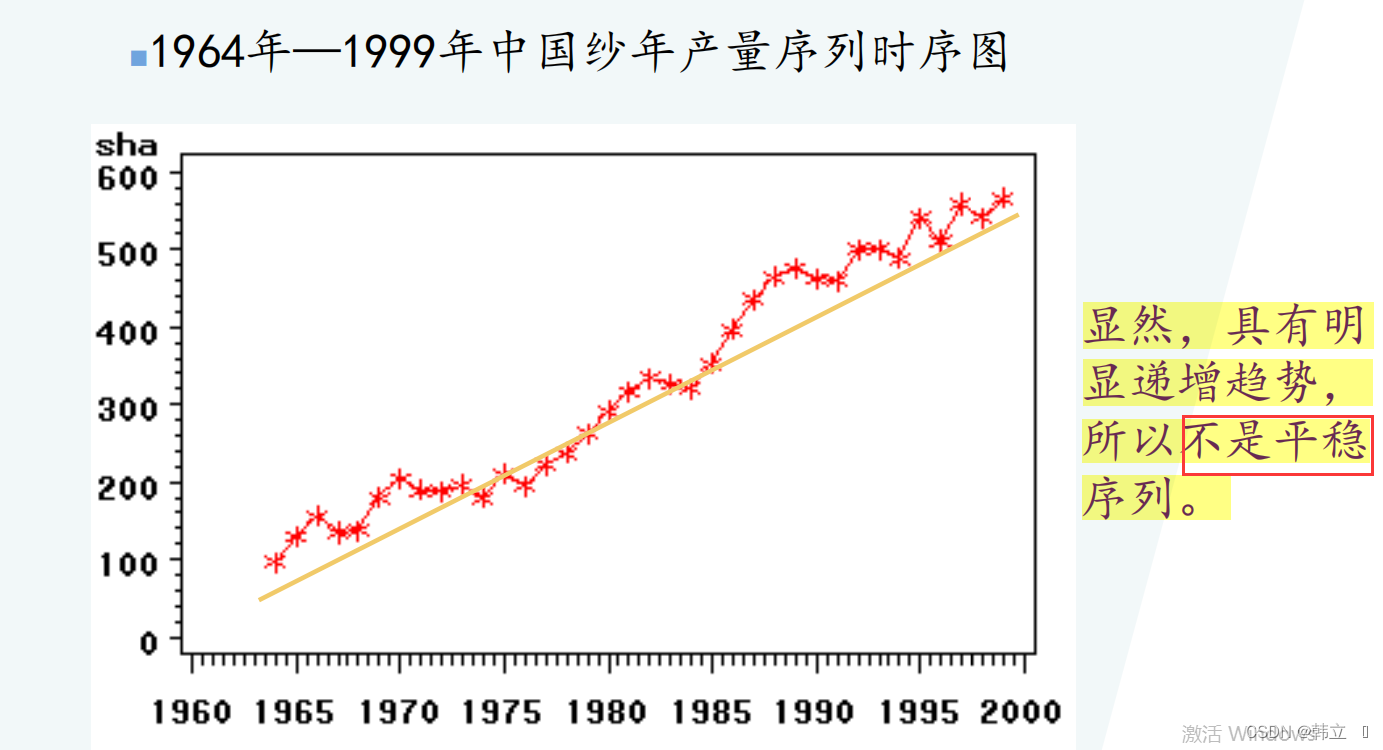
实例:
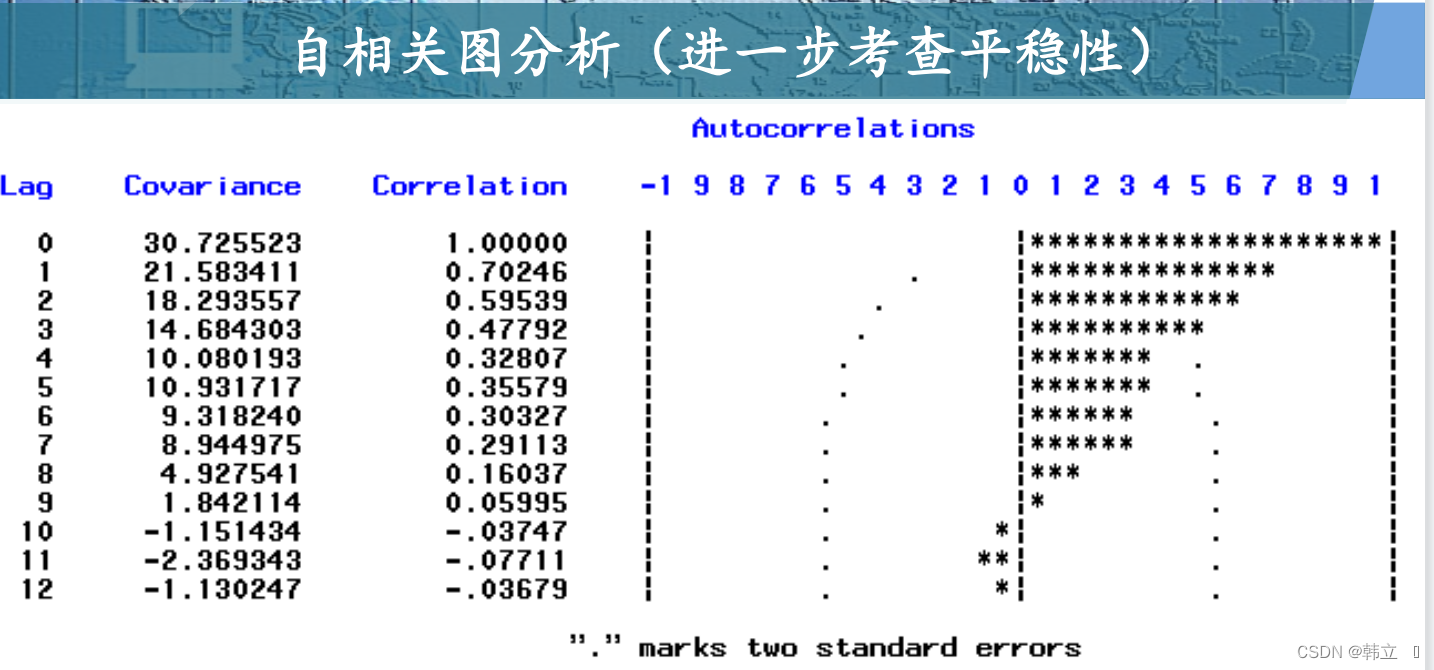
3:自相关检验方法 (随着k的增加):
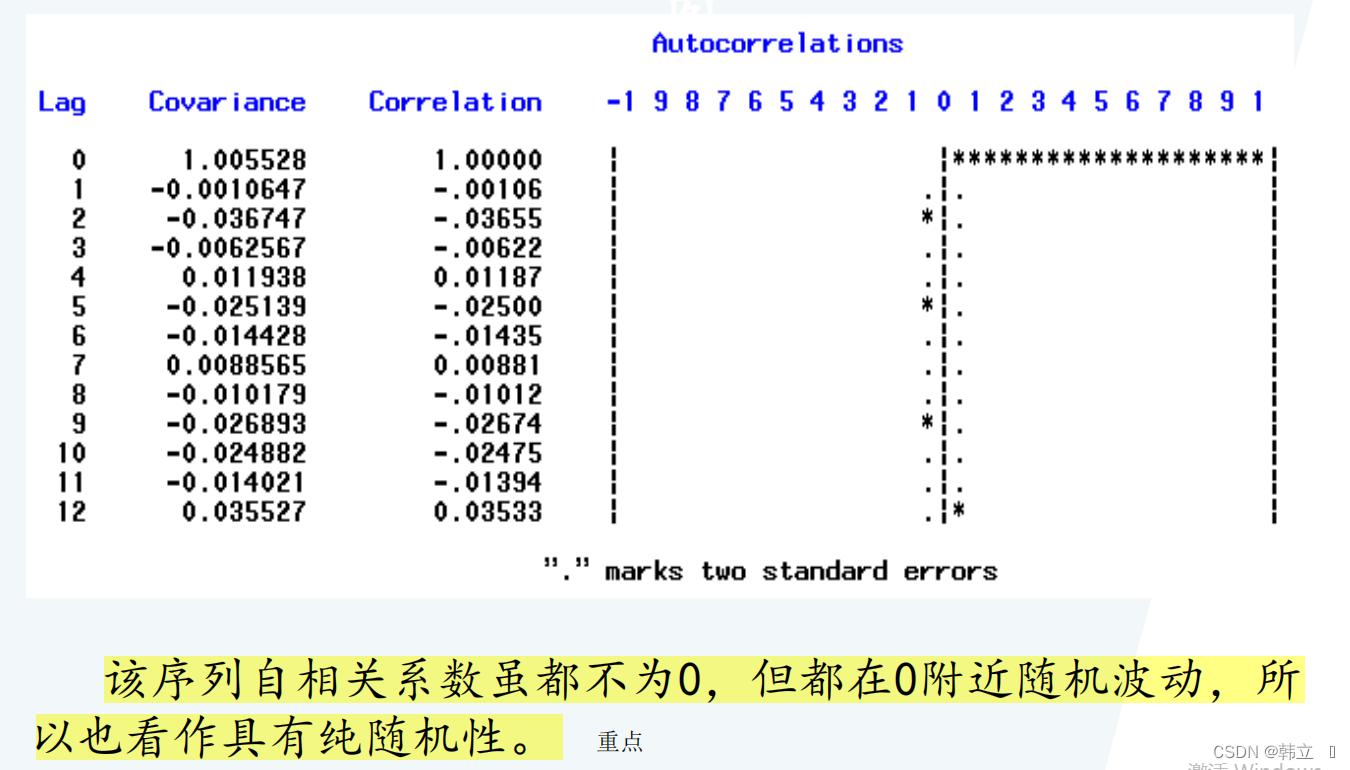
实例:
平稳时间序列的随机性检验:
引出问题:
1:非纯随机性序列定义描述:
2:纯随机序列定义:
2.1:确定性定义:
3:纯随机序列的检验:
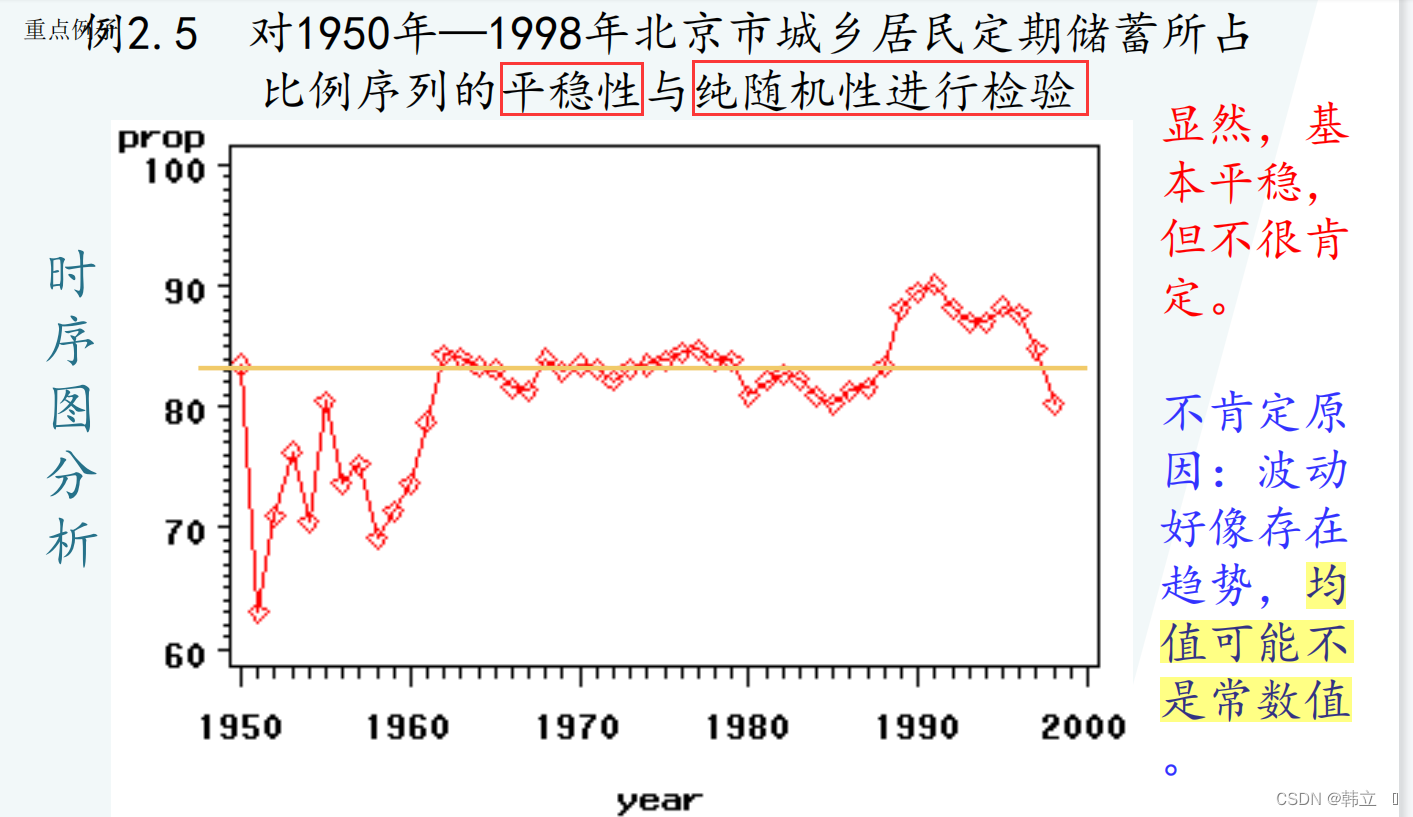
实例:
3.1:更具一般性的检验方法:
首先引出假设检验的方法(概率论数理统计中学习过)
3.2:首先获取分布函数:
3.3:做出假设:
3.4:构建统计量:
3.5:做出判断:
实例:
总结精华(讲了这么多的目的和最终怎么用):总之,我们拿到一个时间序列,我们要做两个检验:
1:平稳性检验:a:时序图法 b:自相关法
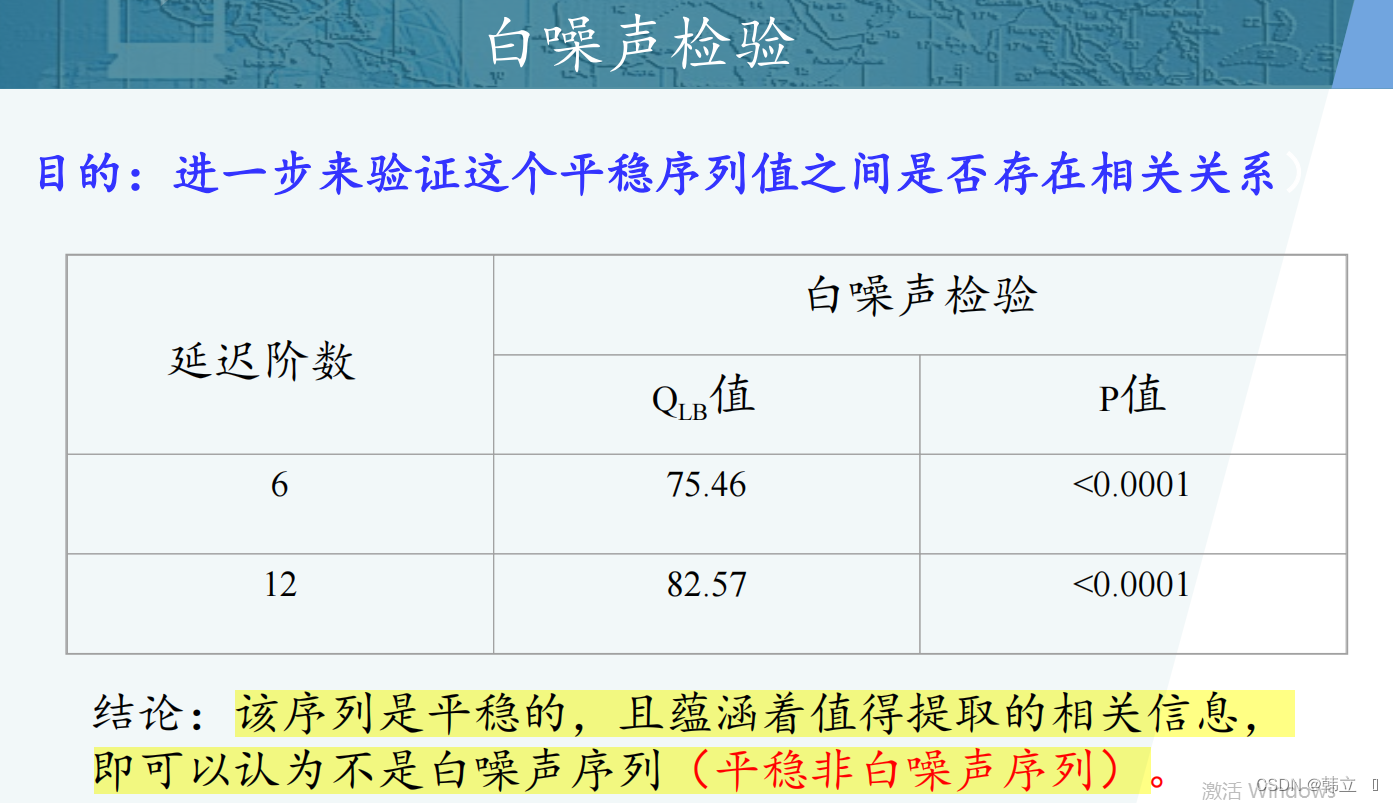
2:纯随机性假设检验:LB检验
实例:
Python实例:
首先,导入数据并且查看:
# 图像显示中文的问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus'] = False
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf
import warnings
warnings.filterwarnings("ignore")
temperature = 'C:\\Users\\Administrator\\Desktop\\数据挖掘项目\\统计学之时序分析案例\\数据源\\arima_data.xls'
data_tem = pd.read_excel(temperature)
plt.figure(figsize=[18, 8])
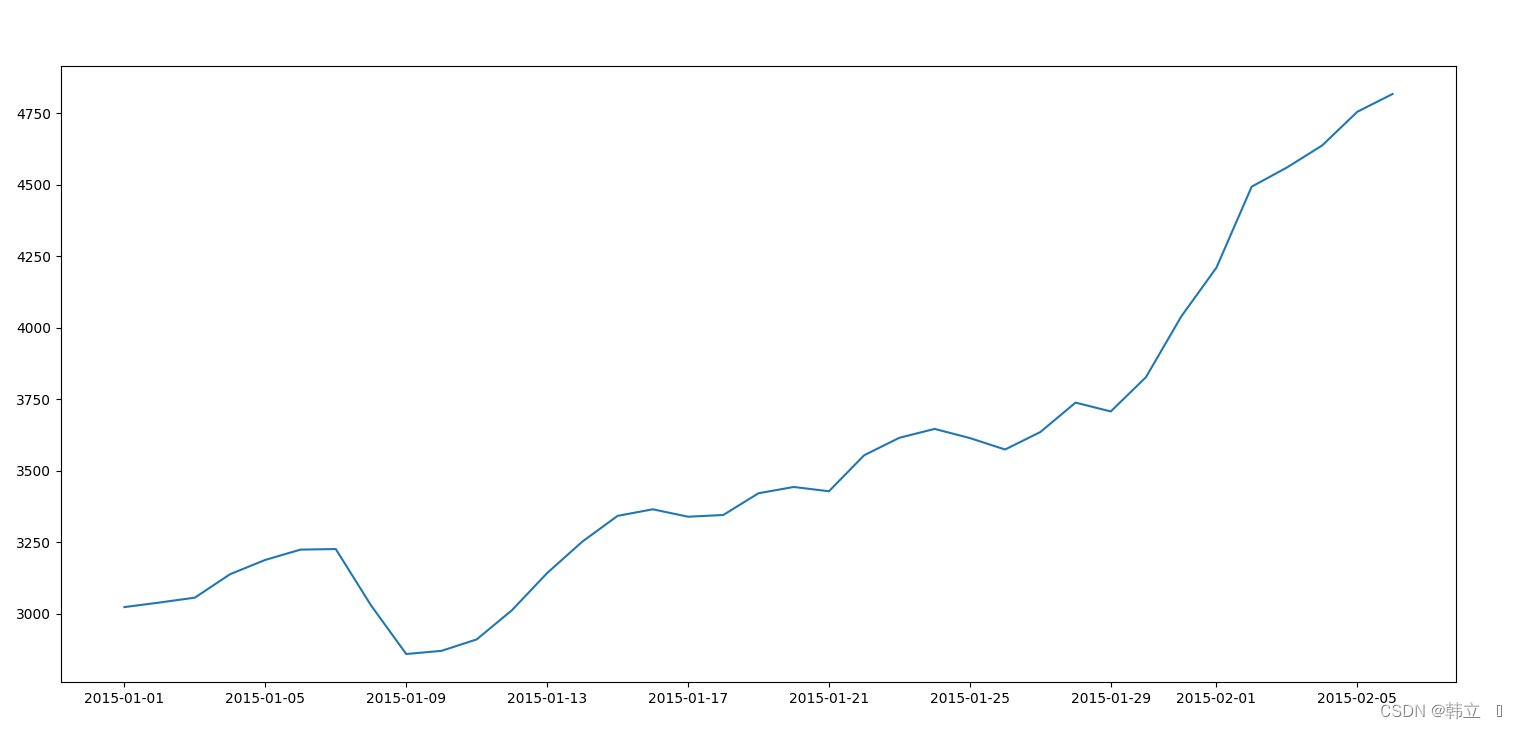
plt.plot(data_tem.日期, data_tem.销量)
plt.show()我们对数据的平稳性并且查看:
自相关检验平稳性 :平稳序列通常具有短期相关性,即随着延迟期数k的增加,平稳序列的自相关系数会很快地衰减向零, 而非平稳序列的自相关系数的衰减速度会比较慢,这就是我们利用自相关图判断平稳性的标准
# 自相关检验平稳性
"""
平稳序列通常具有短期相关性,即随着延迟期数k的增加,平稳序列的自相关系数会很快地衰减向零,
而非平稳序列的自相关系数的衰减速度会比较慢,这就是我们利用自相关图判断平稳性的标准
"""
plt.rcParams.update({'figure.figsize': (8, 6), 'figure.dpi': 100}) # 设置图片大小
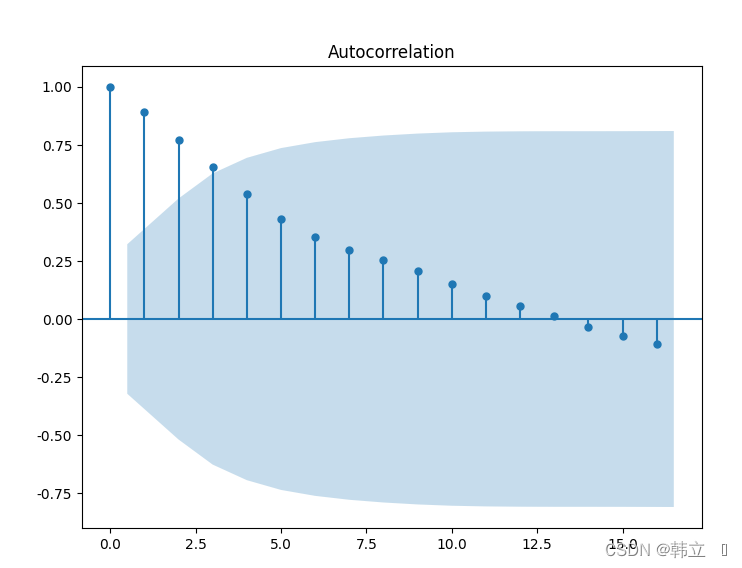
plot_acf(data_tem.销量) # 生成自相关图
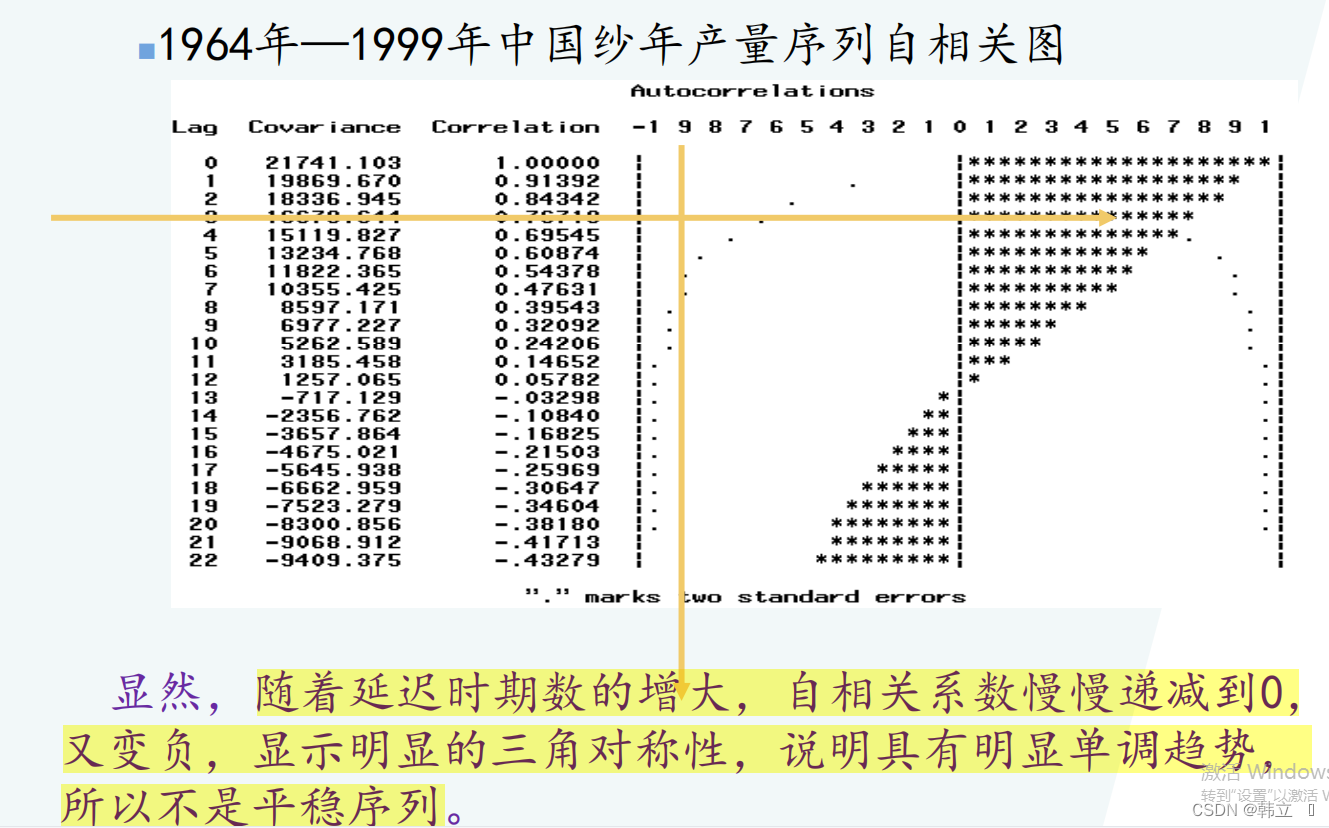
# 自相关系数一直为正,然后为负,呈现出三角对称性,这是具有单调趋势的非平稳序列的一种典型的自相关图形式
plt.show()结论:自相关系数一直为正,然后为负,呈现出三角对称性,这是具有单调趋势的非平稳序列的一种典型的自相关图形式。(后续课程会有更加精确的判断手段)
对数据进行随机性检验:LB随机性检验和Q检验
statsmodels模块中的acorr_ljungbox方法。默认情况下, acorr_ljungbox只计算LB统计量, 只有当参数boxpierce=True时, 才会输出Q统计量。lags参数为延迟参数K
# LB随机性检验
# 白噪声检验Ljung-Box检验
# 该检验用来检查序列是否为随机序列,如果是随机序列,那它们的值之间没有任何关系
# 使用LB检验来检验序列是否为白噪声,原假设为在延迟期数内序列之间相互独立。
LB = sm.stats.diagnostic.acorr_ljungbox(data_tem["销量"], lags=[4, 8], return_df=True)
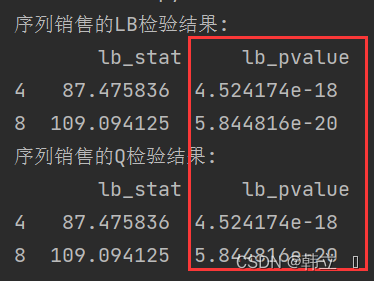
print("序列销售的LB检验结果:\n", LB)
# 如果P值小于0.05,说明序列之间不独立,不是白噪声
# Q随机检验
"""
statsmodels模块中的acorr_ljungbox方法。默认情况下, acorr_ljungbox只计算LB统计量,
只有当参数boxpierce=True时, 才会输出Q统计量。
"""
Q = sm.stats.diagnostic.acorr_ljungbox(data_tem["销量"], lags=[4, 8], return_df=True, boxpierce=False)
print("序列销售的Q检验结果:\n", Q)结论:P值均小于0.05,说明序列之间不独立,不是白噪声,数据具有可预测性
全部代码:
# 图像显示中文的问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus'] = False
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf
import warnings
warnings.filterwarnings("ignore")
temperature = 'C:\\Users\\Administrator\\Desktop\\数据挖掘项目\\统计学之时序分析案例\\数据源\\arima_data.xls'
data_tem = pd.read_excel(temperature)
plt.figure(figsize=[18, 8])
plt.plot(data_tem.日期, data_tem.销量)
plt.show()
# 自相关检验平稳性
"""
平稳序列通常具有短期相关性,即随着延迟期数k的增加,平稳序列的自相关系数会很快地衰减向零,
而非平稳序列的自相关系数的衰减速度会比较慢,这就是我们利用自相关图判断平稳性的标准
"""
plt.rcParams.update({'figure.figsize': (8, 6), 'figure.dpi': 100}) # 设置图片大小
plot_acf(data_tem.销量) # 生成自相关图
# 自相关系数一直为正,然后为负,呈现出三角对称性,这是具有单调趋势的非平稳序列的一种典型的自相关图形式
plt.show()
# LB随机性检验
# 白噪声检验Ljung-Box检验
# 该检验用来检查序列是否为随机序列,如果是随机序列,那它们的值之间没有任何关系
# 使用LB检验来检验序列是否为白噪声,原假设为在延迟期数内序列之间相互独立。
LB = sm.stats.diagnostic.acorr_ljungbox(data_tem["销量"], lags=[4, 8], return_df=True)
print("序列销售的LB检验结果:\n", LB)
# 如果P值小于0.05,说明序列之间不独立,不是白噪声
# Q随机检验
"""
statsmodels模块中的acorr_ljungbox方法。默认情况下, acorr_ljungbox只计算LB统计量,
只有当参数boxpierce=True时, 才会输出Q统计量。
"""
Q = sm.stats.diagnostic.acorr_ljungbox(data_tem["销量"], lags=[4, 8], return_df=True, boxpierce=False)
print("序列销售的Q检验结果:\n", Q)