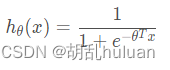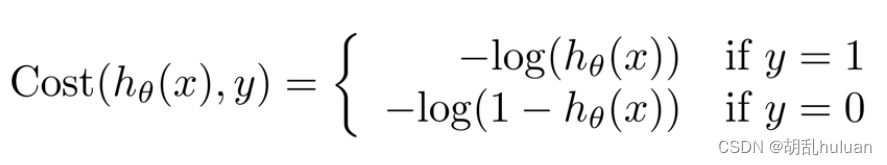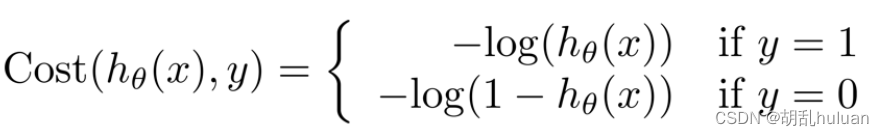机器学习(三)
学习机器学习过程中的心得体会以及知识点的整理,方便我自己查找,也希望可以和大家一起交流。
—— 吴恩达机器学习第五章 ——
四、逻辑回归
-
线性回归局限性
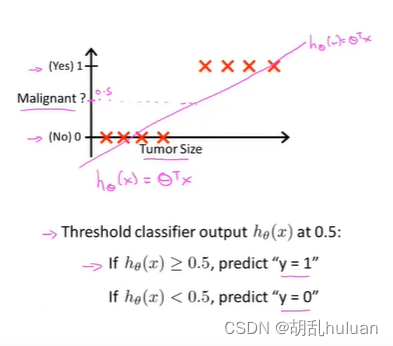
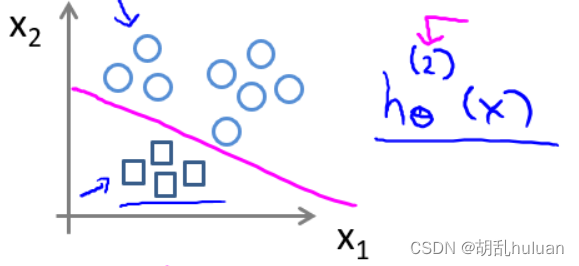
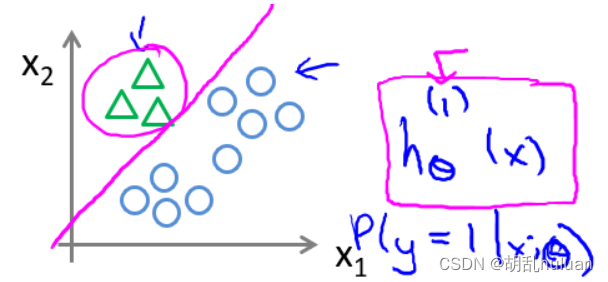
线性回归对于分类问题的局限性:由于离群点的存在,线性回归不适用于分类问题。如下图(阈值为0.5),由于最右离群点,再用线性回归与实际情况不拟合。
因此,我们引入 逻辑回归 算法,来解决这个问题。 -
假设陈述
逻辑回归的假设函数值总是在0到1之间,逻辑回归模型: h θ ( x ) h_{θ}(x) hθ(x), 使得 0 ≤ h θ ( x ) ≤ 1 0 ≤ h_{θ}(x) ≤ 1 0≤hθ(x)≤1 。
在线性回归中, h θ ( x ) = θ T x h_{θ}(x) = θ^{T}x hθ(x)=θTx ,在逻辑回归中令 h θ ( x ) = g ( θ T x ) h_{θ}(x) = g(θ^{T}x ) hθ(x)=g(θTx) ,将 θ x T θ^{T}_{x} θxT带入g(x)得:
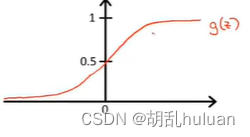
其中 g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1被称为Sigmoid函数,也叫Logistic函数。
h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_{θ}(x)=P ( y=1∣x ;θ ) hθ(x)=P(y=1∣x;θ)( 对于输入的x,y=1的概率估计) -
决策界限
决策边界不是训练集的属性,而是假设本身及其参数的属性。
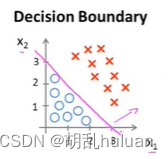
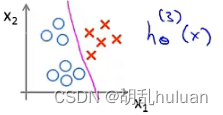
假设有一个训练集: h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 ) h_{θ}(x)=g(θ_{0}+θ_{1}x_{1}+θ_{2}x_{2}) hθ(x)=g(θ0+θ1x1+θ2x2)。用一种方法或者假设,得到参数 θ 0 = − 3 , θ 1 = 1 , θ 2 = 1 θ_{0} = -3,θ_{1} = 1,θ_{2} = 1 θ0=−3,θ1=1,θ2=1。预测 y = 1 i f − 3 + x 1 + x 2 ≥ 0 y = 1 if -3 + x_{1} + x_{2} ≥ 0 y=1if−3+x1+x2≥0,即 x 1 + x 2 ≥ 3 x_{1} + x_{2} ≥ 3 x1+x2≥3。则有下图,中间洋红色直线即为 决策边界 ( x 1 + x 2 = 3 ) (x_{1}+ x_{2} = 3) (x1+x2=3)
其他的例子如下图:
其他参数更多更复杂的也同理。 -
代价函数
将线性回归的代价函数改写为如下形式:
J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 J(θ)=\frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}(h_{θ}(x^{(i)})-y^{(i)})^{2} J(θ)=m1∑i=1m21(hθ(x(i))−y(i))2,进而定义cost函数为 C o s t ( h θ ( x ( i ) , y ( i ) ) = 1 2 ( h θ ( x ( i ) − y ( i ) ) 2 Cost(h_{θ}(x^{(i)},y^{(i)})=\frac{1}{2}(h_{θ}(x^{(i)}-y^{(i)})^{2} Cost(hθ(x(i),y(i))=21(hθ(x(i)−y(i))2
将cost function 运用到逻辑回归中:.
其中 y 表示实际,hθ(x)表示预测。
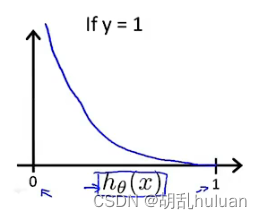
- 当y = 1时:
i f h θ ( x ) = 1 , c o s t = 0 if \ h_{θ}(x) = 1, cost = 0 if hθ(x)=1,cost=0
i f h θ ( x ) = 0 , c o s t = ∞ if \ h_{θ}(x) = 0, cost = ∞ if hθ(x)=0,cost=∞(预测与实际完全不一致,要花费很大的代价惩罚算法)
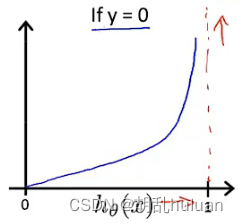
- 当y = 0时:
i f h θ ( x ) = 0 , c o s t = 0 if\ h_{θ}(x) = 0, cost = 0 if hθ(x)=0,cost=0
i f h θ ( x ) = 1 , c o s t = ∞ if\ h_{θ}(x) = 1, cost = ∞ if hθ(x)=1,cost=∞ (预测与实际完全不一致,要花费很大的代价惩罚算法)
- 简化代价函数与梯度下降
将上述式子合并为一个式子: C o s t ( h θ ( x ) , y ) = − y ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) Cost(h_{θ}(x),y)=-y(h_{θ}(x))-(1-y)log(1-h_{θ}(x)) Cost(hθ(x),y)=−y(hθ(x))−(1−y)log(1−hθ(x))
当y = 1时,后一个式子整体为0;当y = 0时,前一个式子整体为0。进而得到:
J ( θ ) = 1 m [ ∑ i = 1 m y ( i ) l o g h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] J(θ)=\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}logh_{θ}(x^{(i)})+(1-y^{(i)})log(1-h_{θ}(x^{(i)}))] J(θ)=m1[∑i=1my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
求最小代价函数由 θ j : = θ j − α ∂ ∂ θ j J ( θ ) θ_{j}:=θ_{j}-\alpha\frac{\partial }{\partial θ_{j} }J(θ) θj:=θj−α∂θj∂J(θ),得 θ j : = θ j − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) θ_{j}:=θ_{j}-\alpha\sum_{i=1}^{m}(h_{θ}(x^{(i)})-y^{(i)})x_{j}^{(i)} θj:=θj−α∑i=1m(hθ(x(i))−y(i))xj(i)。
注意:
- 逻辑回归的代价函数看似与线性回归的代价函数相同,但本质不同。
- 逻辑回归中的 h θ ( x ) = 1 e − θ T x h_{θ}(x)=\frac{1}{e-θ^{T}x} hθ(x)=e−θTx1。
- 线性回归中的 h θ ( x ) = θ T x h_{θ}(x) = θ^{T}x hθ(x)=θTx。
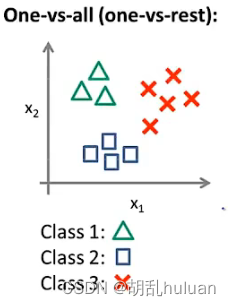
- 逻辑回归解决问题:多元分类
多元分类即结果有多种可能。如下图,有三种可能结果。
将它们两两作为一组,方法是将其中一个类别作为正类,其他作为负类,依次建立新的训练集,得到
即为 h θ ( i ) ( x ) = P ( y = i ∣ x ; θ ) ( i = 1 , 2 , 3 ) h_{θ}^{(i)}(x)=P(y=i|x;θ)\ (i=1,2,3) hθ(i)(x)=P(y=i∣x;θ) (i=1,2,3),最后需要输入一个x,选择h最大的类别,也即在三个分类器中选择可信度最高,效果最好的。