冒泡排序及其三种写法

冒泡排序

冒泡排序是入门级的算法，但也有一些有趣的玩法。

通常来说，冒泡排序有三种写法：

一边比较一边向后两两交换，将最大值/最小值冒泡到最后一位；

经过优化的写法：使用一个变量记录当前轮次的比较是否发生过交换，

如果没有发生交换表示已经有序，不再继续排序

进一步优化的写法：除了使用变量记录当前轮次的是否发生交换外，

再使用一个变量记录上一次发生交换的位置，下一轮排序时，

到达上一次交换的位置就停止比较

冒泡排序的第一种写法

private static void bubbleSort(int[] arr) {
		for(int i=0;i<arr.length-1;i++) {
			for(int j=0;j<arr.length-1-i;j++) {
				if (arr[j]>arr[j+1]) {
					//如果左边的数大于右边的数，则交换，保证右边的数字最大
					swap(arr, j, j+1);
				}
			}
		}
	}
//交换元素
	private static void swap(int[] arr,int i,int j) {
		int temp=arr[i];
		arr[i]=arr[j];
		arr[j]=temp;
	}

最外层的 for 循环每经过一轮，剩余数字中的最大值就会被移动到当前轮次的最后一位，中途也会有一些相邻的数字经过交换变得有序。

这种写法相当于相邻的数字两两比较，并且规定：“谁大谁站右边”。

整个过程看起来就像一个个气泡不断上浮，这也是“冒泡排序法”名字的由来。

冒泡排序的第二种写法

private static void bubbleSort(int[] arr) {
		//初始化swapped为true，否则排序过程无法启动
		boolean swapped =true;
		for (int i = 0; i < arr.length-1; i++) {
			//如果没有发生过交换，说明剩余部分已经有序，排序完成
			if (!swapped) {
				break;
			}
			//设置swapped为false，如果发生交换则将其设置为true
			swapped=false;
			for (int j = 0; j < arr.length-1-i; j++) {
				if (arr[j]>arr[j+1]) {
					//如果左边的数大于右边的数，则交换，保证右边的数字最大
					swap(arr, j, j+1);
					//表示发生了交换
					swapped=true;
				}
			}
		}
	}
//交换元素
	private static void swap(int[] arr,int i,int j) {
		int temp=arr[i];
		arr[i]=arr[j];
		arr[j]=temp;
	}

最外层的 for 循环每经过一轮，剩余数字中的最大值仍然是被移动到当前轮次的最后一位。

这种写法相对于第一种写法的优点是：如果一轮比较中没有发生过交换，则立即停止排序，因为此时剩余数字一定已经有序了。

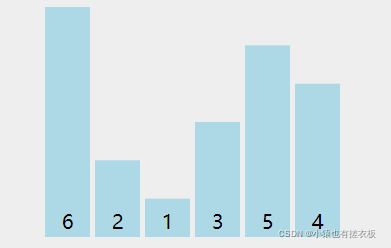
图中可以看出：

第一轮排序将数字 6 移动到最右边；
第二轮排序将数字 5 移动到最右边，同时中途将 1 和 2 排了序；
第三轮排序时，没有发生交换，表明排序已经完成，不再继续比较。

冒泡排序的第三种写法

public static void bubbleSort(int[] arr) {
		boolean swapped = true;
		// 最后一个没有经过排序的元素的下标
		int indexOfLastUnsortedElement = arr.length - 1;
		// 上次发生交换的位置
		int swappedIndex = -1;
		while (swapped) {
			swapped = false;
			for (int i = 0; i < indexOfLastUnsortedElement; i++) {
				if (arr[i] > arr[i + 1]) {
					// 如果左边的数大于右边的数，则交换，保证右边的数字最大
					swap(arr, i, i + 1);
					// 表示发生了交换
					swapped = true;
					// 更新交换的位置
					swappedIndex = i;
				}
			}
			// 最后一个没有经过排序的元素的下标就是最后一次发生交换的位置
			indexOfLastUnsortedElement = swappedIndex;
		}
	}
	// 交换元素
	private static void swap(int[] arr, int i, int j) {
		int temp = arr[i];
		arr[i] = arr[j];
		arr[j] = temp;
	}

经过再一次的优化，代码看起来就稍微有点复杂了。

最外层的 while 循环每经过一轮，剩余数字中的最大值仍然是被移动到当前轮次的最后一位。

在下一轮比较时，只需比较到上一轮比较中，最后一次发生交换的位置即可。因为后面的所有元素都没有发生过交换，必然已经有序了。

当一轮比较中从头到尾都没有发生过交换，则表示整个列表已经有序，排序完成。