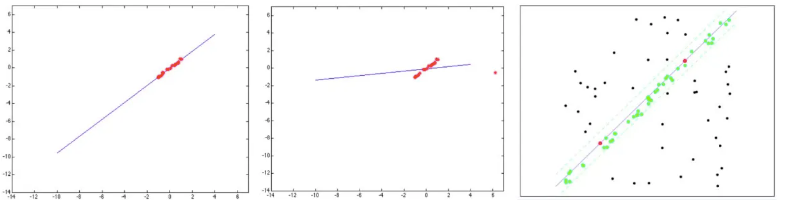
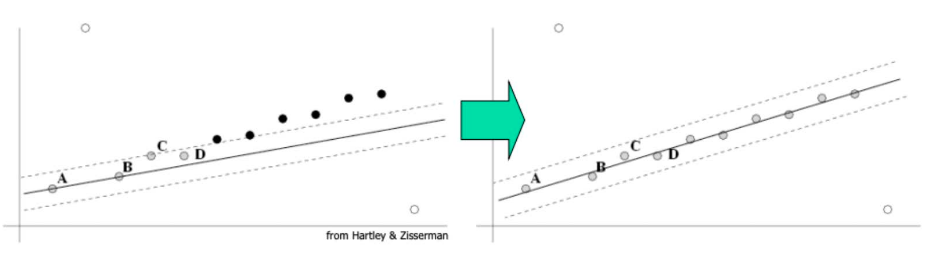
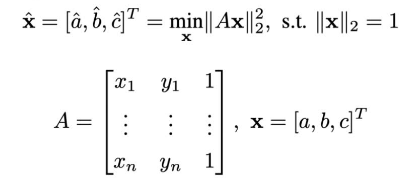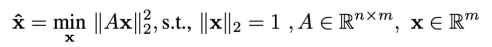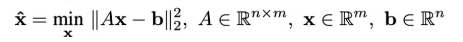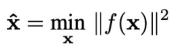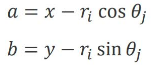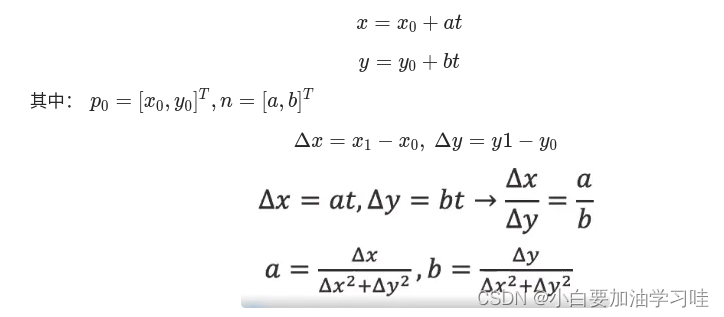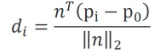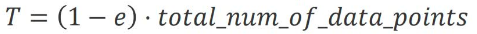以直线拟合为例,模型拟合常用的方法有Least Square(最小二乘)、Hough Transform(霍夫变换)、Random Sample Consensus(RANSAC)等。那么该如何区分和使用这几种方法呢?
- 情况1:已知 inlier 点,即已知哪些点可以用来拟合模型;(最小二乘)
- 情况2:如果数据中存在少量outliers?(①Robust 最小二乘,对loss fuction进行修改;②Hough变换; ③RANSAC;)
- 情况3:如果数据中存在大量outliers或者待拟合的模型不止一种?(①Hough变换;②RANSAC)
1. 最小二乘
目标:给定一堆数据点
{
p
1
,
p
2
,
.
.
.
,
p
n
}
\{p_1,p_2,...,p_n \}
{p1,p2,...,pn},如何找到一个和这些数据点最匹配的直线方程?
模型:
a
x
+
b
y
+
c
=
0
ax+by+c=0
ax+by+c=0
损失函数:
E
=
∑
i
=
1
n
(
a
x
i
+
b
y
i
+
c
)
2
E=\sum_{i=1}^n (ax_i+by_i+c)^2
E=i=1∑n(axi+byi+c)2
其中:
a
x
i
+
b
y
i
+
c
ax_i+by_i+c
axi+byi+c表示点
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi)到拟合直线的距离。
求解损失函数:
1.1 最小二乘的几种形式:
-
Ax=0
解为 A的最小特征值的特征向量(前提是A是一个列满秩矩阵,即 n ≥ m); -
Ax=b
解为 x ^ = ( A T A ) − 1 A T b \hat{x} = (A^T A)^{-1} A^Tb x^=(ATA)−1ATb(前提是A是一个列满秩矩阵,即 n ≥ m); -
Ax=b, s.t., Cx = 0
解法可以使用 拉格朗日乘值法。
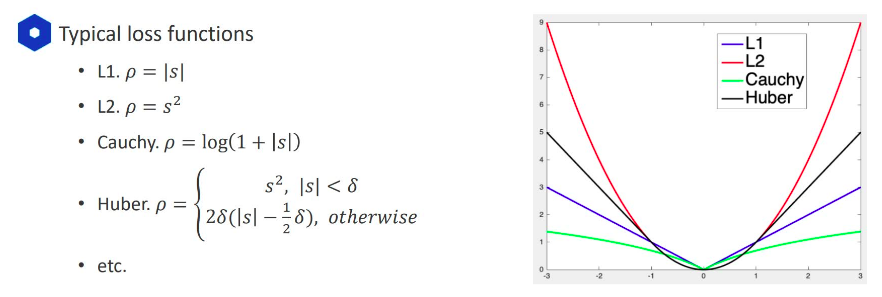
1.2 Robust最小二乘
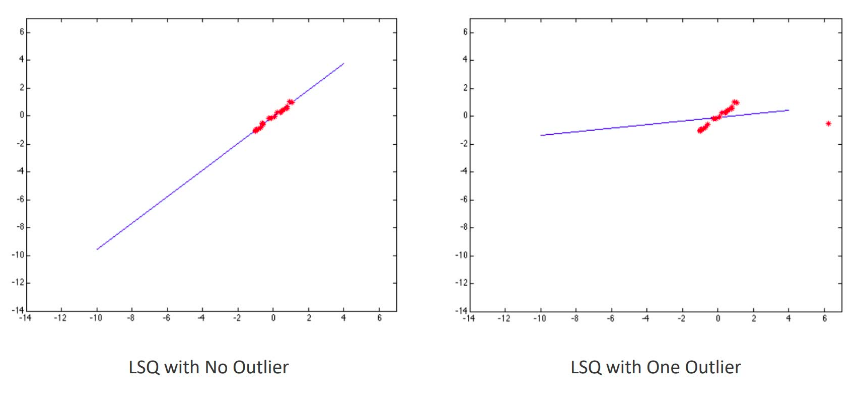
由于最小二乘对噪声比较敏感:
因此提出了Robust最小二乘:
因为当待拟合数据中存在噪声点时,
(
a
x
i
+
b
y
i
+
c
)
(ax_i + by_i + c)
(axi+byi+c)平方的值会比较大,因此采用 |s| 或取对数的方式来减小误差值,像Cauchy, Huber这样的鲁棒损失函数减少了异常值的影响。但此时这样的损失函数形式会导致问题不再是线性的,就无法直接使用最小二乘求解。
解决方法:
将Robust损失函数和线性LSQ耦合,满足最小二乘形式即可:
优化方法:
Gradient descent(梯度下降法)、Gauss-Newton(高斯牛顿法)、Levenberg-Marquardt(LM)
总结:
最小二乘法简单、速度快,但是对噪声比较敏感,无法拟合多个模型;
2. Hough变换
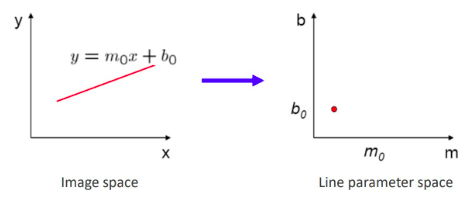
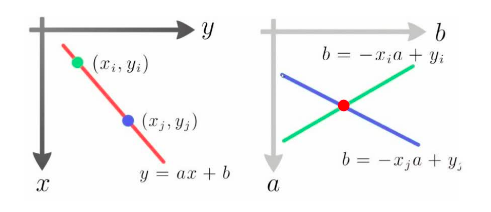
核心思想:原始空间的点可以转化为参数空间的线,或者参数空间的线可以转化成原始空间的点。
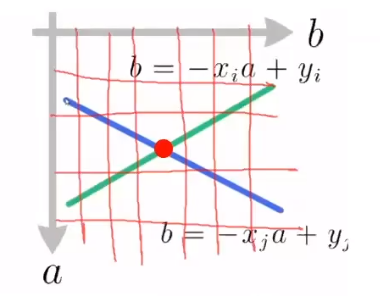
当原始空间的函数相对复杂,无法直接获取参数k空间的交点时,可以使用 投票(most votes)的方式。如下图所示,以参数分辨率为最小单元建立网格,假设:
在a方向:对于a=0.1,计算b=0.21,此时向下取整后标记(0.1, 0.2)对应的网格;同样的,对于a=0.2,计算b=0.26,标记(0.2, 0.2)对应的网格;
在b方向:同样以最小分辨率标记对应网格。
最终遍历所有网格点,存在两个标记点的网格点就是参数空间下的交点。(参数的准确性与网格的分辨率有关)
需要注意的是,直线方程
y
=
a
x
+
b
y=ax+b
y=ax+b是不均匀的,无法表示垂直线(a为无穷大的情况),因此考虑采用模型参数化的方法:
x
c
o
s
(
θ
)
+
y
s
i
n
(
θ
)
=
r
x cos(\theta) + y sin(\theta) = r
xcos(θ)+ysin(θ)=r
其中,
θ
,
r
\theta, r
θ,r表示模型参数。
同样的采用投票(most votes)的方式,分别固定 r 和 𝜃。如果需要更高的精度,可以提高分辨率 r ,如果需要更快的速度,可以提高𝜃。
小技巧:在搜索最高投票参数之前,可以在参数空间做一个高斯模糊,减少噪声的影响。
2.1 如果有3个参数呢?
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
(x-a)^2 + (y-b)^2 = r^2
(x−a)2+(y−b)2=r2
步骤1:首先固定 r,设定最小的分辨率;
步骤2:均匀地对 𝜃 进行采样
{
θ
1
,
θ
2
,
.
.
.
,
θ
k
}
\{\theta_1,\theta_2,...,\theta_k \}
{θ1,θ2,...,θk};
步骤3:用 𝜃 表示参数 a、b
步骤4:搜索投票为3的网格区域
总结-优点:
对噪声不敏感、所要求的数据点形状可以是不完整的、可以扩展到多种模型;
总结-缺点:
无法对多个参数进行拟合(一般只用在二维和三维空间,即模型参数在2-3个的情况下)。
3. RANSAC
RANSAC模型拟合的效果与数据中inlier点的比例有关,且对模型参数的个数无明确要求。
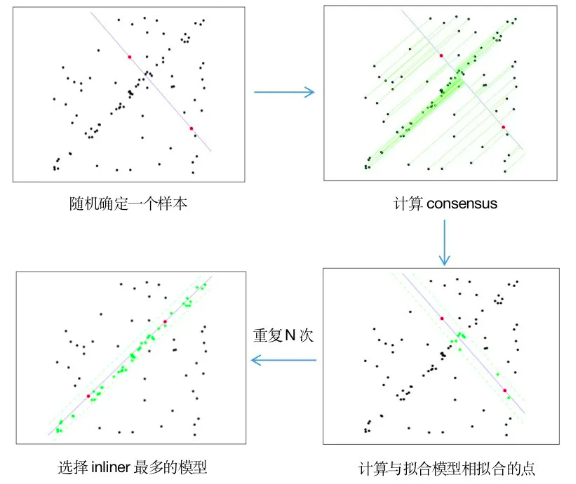
基本思路:以求解模型所需的最小数据子集为标准进行采样。
- 随机选取一个样本(通常为求解模型参数所需的最小子集,如直线模型需要两个样本点)
p 0 = ( x 0 , y 0 ) , p 1 = ( x 1 , y 1 ) p_0=(x_0,y_0), \space p1=(x_1,y_1) p0=(x0,y0), p1=(x1,y1) - 计算模型参数:
- 计算Consensus,即每个点 p i = ( x i , y i ) p_i =(x_i,y_i) pi=(xi,yi)的误差函数:
- 计算与当前模型相拟合的数据点,即“模型的支持者”: d i < τ ( i n l i e r ) d_i < \tau(inlier) di<τ(inlier)
- 重复迭代步骤1-4 N次,选择inlier最多的模型。
3.1 RANSAC参数选择
RANSAC模型拟合过程中有两个参数需要确认:距离阈值 τ 和迭代次数 N。
- 距离阈值(τ)的选取:
一般通过实验测试得到 d,当然也可以通过卡方分布(Chi-square distribution
χ
2
\chi^2
χ2)计算得到理论值(但该方法不实用,因为实际问题中通常无法提前知道数据分布信息)。
卡方分布:k 个独立的标准高斯分布的和。
假设每个数据点到模型的距离符合高斯分布
d
∼
N
(
0
,
σ
2
)
d \sim N(0,\sigma^2)
d∼N(0,σ2)。假设希望95%的置信度来认为一个点是inlier点,那么 τ 的取值受卡方分布参数 k的 自由度的影响:
- 迭代次数(N)的选取:
选择一个N,使得N次迭代后,至少有一个模型没有outliers的概率 p,比如目标概率p=0.9/0.99 (取决于希望模型迭代 更快速or更准确)。
如何确定N?
- e:outlier ratio(所有数据点中outlier部分的比例)
- s:模型解算所需的最少数据点数(如直线拟合需要最少2个点)
- N:迭代次数
- p:执行N次迭代后,至少有一个模型没有outlier的概率,即至少拿到一个好的sample的概率;
N
=
l
o
g
(
1
−
p
)
l
o
g
(
1
−
(
1
−
e
)
s
)
N=\frac{log(1-p)}{log(1-(1-e)^s)}
N=log(1−(1−e)s)log(1−p)
其中,比较关键的信息是数据点的outlier ratio — e。
3.2 应用技巧
-
提前终止迭代:(如当前拟合模型的inlier ratio已经达到了预期的效果)
即满足 T n t o t a l ≥ 1 − e \frac{T}{n_{total}} \ge 1-e ntotalT≥1−e时就可以提前终止了。 -
RANSAC + LSQ:使用RANSAC粗拟合获取inlier,再对inlier使用LSQ对模型进行优化。
总结-优点:
简单、通用性强,通常在实践中效果较好,在inlier ratio较低时也可以取得较好的效果;
总结-缺点:
需要进行多次实验来选取 τ,当inlier ratio很低时,迭代次数较多。
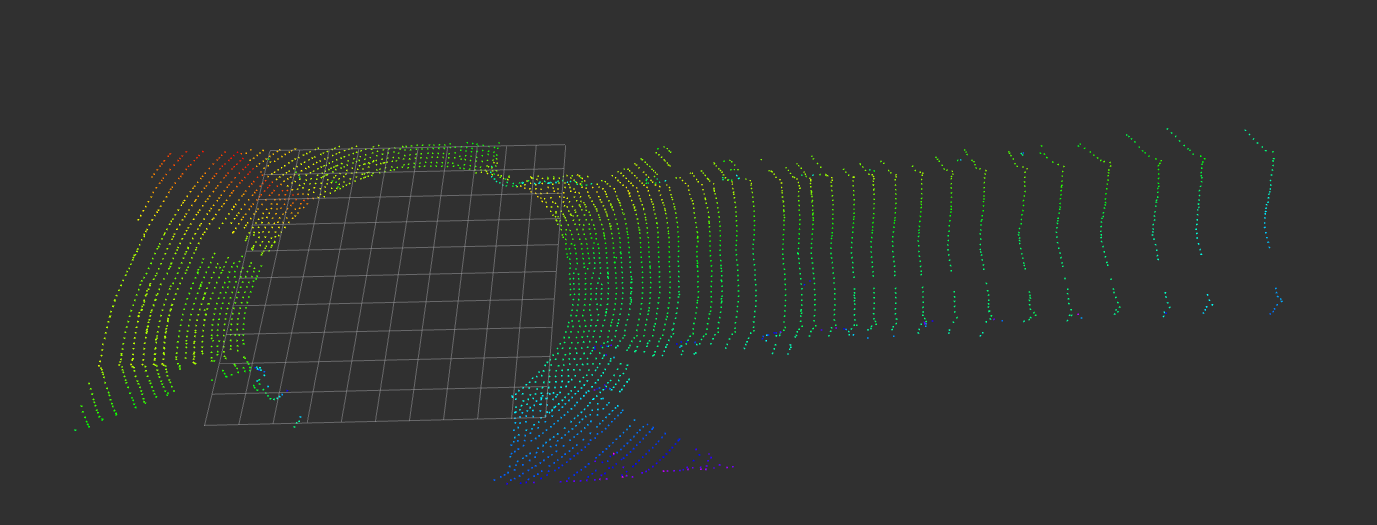
4. 实践练习
基于Kitti数据集激光雷达点云数据,利用RANSAC方法拟合地面,筛选地面点和非地面点,并对非地面点进行聚类及可视化。
-
原始点云
-
感兴趣区域点云提取
-
地面点云提取
-
障碍物点云聚类
障碍物聚类-Peek 2024-05-07 19-00
参考链接: