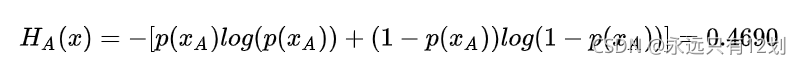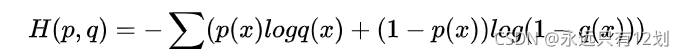2021SC@SDUSC

文本分类半监督学习分析代码来源：

GitHub - SanghunYun/UDA_pytorch: UDA(Unsupervised Data Augmentation) implemented by pytorchhttps://github.com/Sanghunyun/UDA_pytorch该项目（无标签数据增强）整体思路见下图：

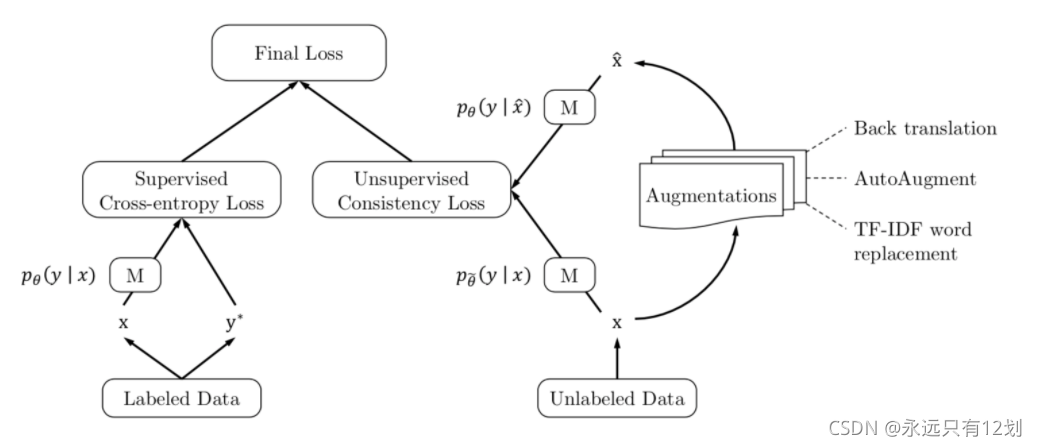
1.计算模型训练损失

该模型训练的损失分为有标签和无标签数据造成的损失两部分，由图中可以看出分别使用交叉熵和相对熵进行计算。

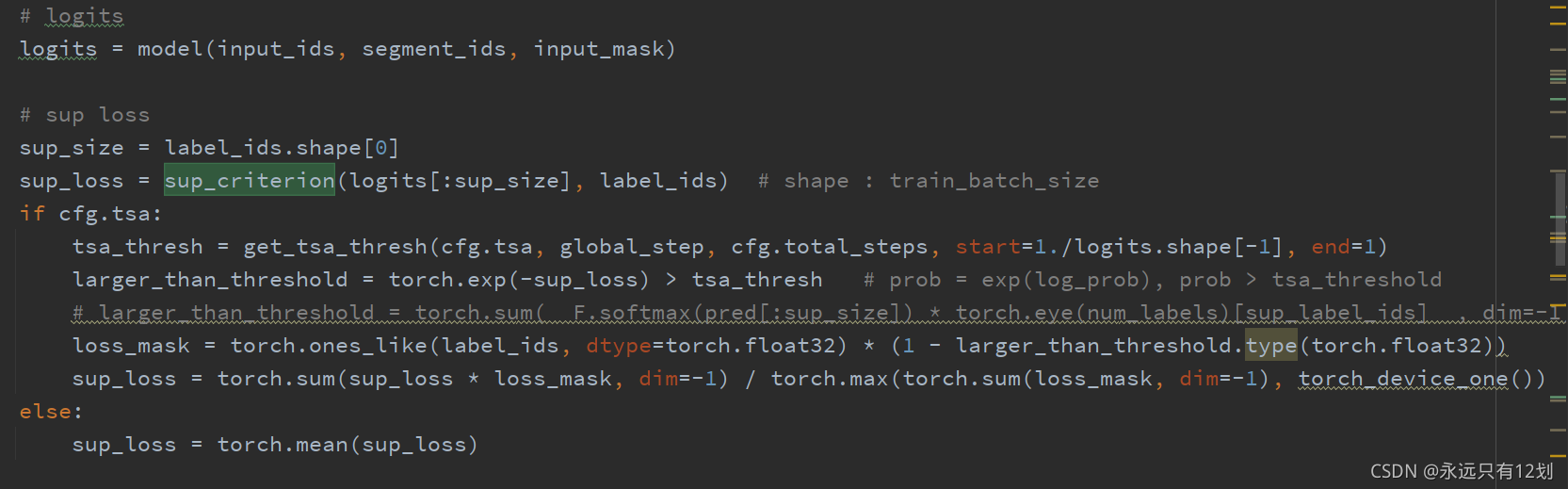
代码中体现如下：

uda_mode设置为True表示需要计算两种损失

以交叉熵计算有标签数据损失为例，解析原理：

信息量：它是用来衡量一个事件的不确定性的；一个事件发生的概率越大，不确定性越小，则它所携带的信息量就越小。假设X是一个离散型随机变量，其取值集合为X，概率分布函数为  ，我们定义事件  的信息量为：  当  时，熵将等于0，也就是说该事件的发生不会导致任何信息量的增加。

熵：它是用来衡量一个系统的混乱程度的，代表一个系统中信息量的总和；信息量总和越大，表明这个系统不确定性就越大。

    举个例子：假如小明和小王去打靶，那么打靶结果其实是一个0-1分布，X的取值有{0：打中，1：打不中}。在打靶之前我们知道小明和小王打中的先验概率为10%，99.9%。根据上面的信息量的介绍，我们可以分别得到小明和小王打靶打中的信息量。但是如果我们想进一步度量小明打靶结果的不确定度，这就需要用到熵的概念了。那么如何度量呢，那就要采用期望了。我们对所有可能事件所带来的信息量求期望，其结果就能衡量小明打靶的不确定度

 与之对应的，小王的熵（打靶的不确定度）为： 虽然小明打靶结果的不确定度较低，毕竟十次有9次都脱靶；但是小王打靶结果的不确定度更低，1000次射击只有1次脱靶，结果相当的确定。

交叉熵：它主要刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。假设概率分布p为期望输出，概率分布q为实际输出，  为交叉熵，则

因此代码中logits数组存储了sup_size大小的预测值，将其与真实值label_ids一起传入sup_criterion()中计算损失。

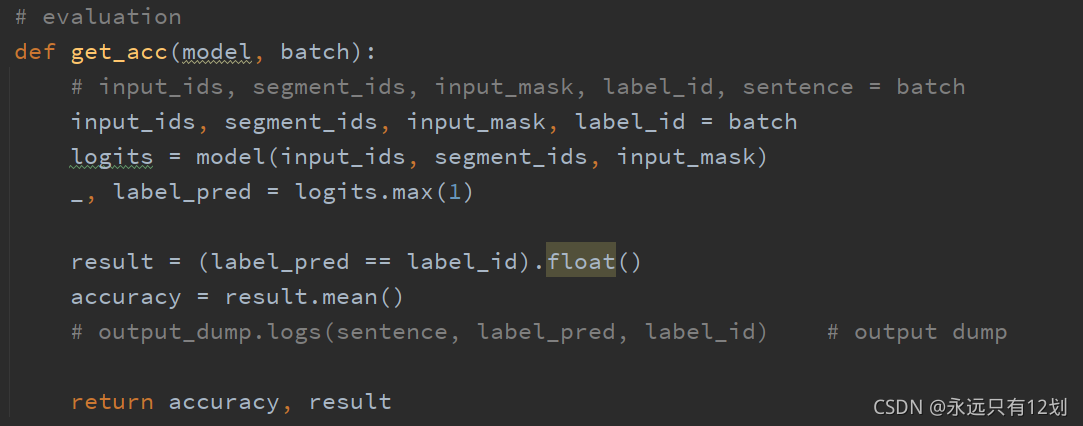
2.精度计算

同样logits是模型结果，精度计算则为结果与真实值label_id相同的个数。