1

1. 什么是线性回归？

线性回归是机器学习中最基础且广泛使用的回归算法之一，用于预测因变量（目标变量）和一个或多个自变量（特征变量）之间的线性关系。它通过找到一条最佳拟合直线，最小化数据点与直线之间的误差来进行预测。

数学形式上，线性回归试图拟合一个线性函数：

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_n{x}_n+ϵ$$

其中：

• ( y ) 是目标变量（因变量）。
• ($x_1$, $x_2$, $\dots$, $x_n$) 是自变量（特征变量）。
• ( ${\beta }_0$ ) 是截距，表示当所有自变量为零时，目标变量的预测值。
• ( ${\beta }_1$, ${\beta }_2$, $\dots$, ${\beta }_n$ ) 是回归系数，表示每个自变量对目标变量的线性影响。
• ( $ϵ$) 是误差项，表示模型无法解释的部分。

2. 线性回归的目标

线性回归的目标是找到最佳的权重 ( $w$ ) 和偏置 ( $b$ )，使得模型预测的值与真实值之间的差异（即损失函数）最小。求解线性回归模型最常用的方法是普通最小二乘法（Ordinary Least Squares, OLS），它通过解析的方式直接计算权重和偏置。常用的损失函数是均方误差（Mean Squared Error, MSE。
普通线性最小二乘法（Ordinary Least Squares, OLS）和残差平方和（Residual Sum of Squares, RSS）是两个相关但不同的概念，它们在回归分析中发挥着不同的作用。

（1）. 普通最小二乘法（OLS）

普通线性最小二乘法是一种统计方法，用于估计线性回归模型的参数。其核心思想是通过最小化残差平方和来找到最佳的回归系数。这种方法假设因变量和自变量之间存在线性关系，目标是找出最能描述这种关系的线性方程。

OLS的步骤：

• 定义线性模型：( $y$ = ${\beta }_0$ + ${\beta }_1{x}_1$ + ${\beta }_2{x}_2$ + $\dots$ + ${\beta }_n{x}_n$ + $ϵ$ )
• 计算每个观测值的残差：( $e_i$ = $y_i$ - ${\hat{y}}_i$ )，其中 ( ${\hat{y}}_i$ ) 是通过模型预测的值。
• 最小化残差平方和：( $RSS$ = ${\sum }_{i=1}^N(y_i-{\hat{y}}_i{)}^2$ )(损失函数)

求解RSS的步骤：

在线性回归中，损失函数帮助确定决策边界。在二分类问题中，逻辑回归同样使用损失函数（交叉熵损失）来衡量预测概率与实际标签之间的差异，从而形成决策边界。

通过求解RSS的偏导数并设为零，可以得到回归系数的估计值。
为了最小化 RSS，我们需要对 RSS 关于每个参数 ($\beta$) 进行偏导数求解，并将结果设为零。这可以通过以下步骤实现：

0. 损失函数的优化：
   $${\beta }_j={\beta }_j-\alpha \frac{\partial L}{\partial {\beta }_j}$$通过最小化损失函数，我们可以找到最优的模型参数（回归系数）。这通常涉及以下步骤：

• 计算损失值：根据当前模型参数计算损失函数的值。
• 优化算法：使用梯度下降、牛顿法等优化算法，调整参数以减小损失值。例如，梯度下降通过以下公式迭代更新参数：

其中 ( $\alpha$ ) 是学习率，表示每次更新的幅度(步长)。

1. 对每个参数求偏导数：
   • 例如，对于 (${\beta }_j$)：

$$\frac{\partial RSS}{\partial {\beta }_j}=-2\sum _{i=1}^N(y_i-{\hat{y}}_i)x_{ij}$$

2. 设偏导数为零：
   • 得到一组方程，称为正态方程：

$$\sum _{i=1}^N(y_i-{\hat{y}}_i)x_{ij}=0$$

3. 矩阵表示法：

为了方便求解，可以使用矩阵形式来表示线性回归模型。设设计矩阵 (X) 和目标向量 (y)：

$$X=\left[\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_{1n}\\ 1& x_{21}& x_{22}& \cdots & x_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_{N1}& x_{N2}& \cdots & x_{Nn}\end{array}\right]$$

$$y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_N\end{array}\right]$$

3. 回归系数的求解：

对于多元线性回归，回归系数的估计可以通过矩阵形式表示：
$$\beta =(X^{T}X{)}^{-1}{X}^{T}y$$

其中：

• ( $X$ ) 是包含自变量的设计矩阵，第一列为1（表示截距项）。
• ( $y$ ) 是因变量的观测值向量。

（2）. 残差平方和（RSS）

①. 定义

残差平方和是一个衡量模型拟合效果的指标。它表示实际观测值与模型预测值之间差异的平方和，反映了模型预测的误差。RSS越小，说明模型的预测效果越好。

RSS的公式：
$$RSS=\sum _{i=1}^N(y_i-{\hat{y}}_i{)}^2$$
其中：

• ( $y_i$ ) 是第 ( $i$ ) 个观测值（实际值）。
• ( ${\hat{y}}_i$) 是通过模型预测的第 ( $i$) 个值。
• ( $N$ ) 是总观测数。
  残差平方和是衡量线性回归模型准确性的一种重要指标。它反映了模型预测值与实际观测值之间的差异。

②. 衡量模型准确性的方式

• 误差的度量：RSS 量化了模型的预测误差，越小的 RSS 表示模型的预测值与实际值越接近，表明模型的拟合效果越好。
• 反映模型的健壮性：如果 RSS 很大，说明模型未能有效捕捉数据的趋势，可能是由于模型的选择不当（如遗漏了重要变量、选择了不合适的模型等）。
• 用于模型比较：在比较不同模型的拟合效果时，RSS 可以作为一个指标，通常选择 RSS 较小的模型作为更优的模型。

③. 限制

尽管 RSS 是衡量模型准确性的一个重要指标，但它并不是唯一的标准，其局限性包括：

• 对样本大小敏感：RSS 的绝对值受到样本大小的影响，较大的样本可能导致较大的 RSS。因此，在比较模型时，通常需要标准化（如均方误差 MSE）。
• 未考虑模型复杂性：仅依赖 RSS 可能导致过拟合，因为复杂模型可能在训练数据上获得较小的 RSS，但在新数据上的泛化能力较差。

④. 相关指标

为了克服 RSS 的一些局限性，通常会使用其他指标进行补充评估：

• 均方误差（MSE）：MSE 是 RSS 除以样本数量 ( $N$ )，它提供了平均预测误差。
  $$MSE=\frac{RSS}{N}$$

• 决定系数（R²）：R² 衡量模型解释的方差比例，范围在 0 到 1 之间。它可以帮助判断模型对数据变异的解释能力。其计算方式如下：
  $$R^2=1-\frac{RSS}{TSS}$$
  MSE越小越好，R² 越接近1越好
  其中：

• ( RSS ) 是残差平方和，表示模型预测值与实际值之间的差异。

• ( TSS ) 是总平方和， $TSS$ = ${\sum }_{i=1}^N(y_i-\bar{y}{)}^2$。表示实际值与实际均值之间的总变异。

• R² 的值范围：R² 的值范围在 0 到 1 之间。

  • ( $R^2$ = 1 ) 表示模型完美拟合，所有预测值与实际值完全相等。
  • ( $R^2$ = 0 ) 表示模型没有解释任何方差，模型的预测效果不佳。

• R² < 0：在某些情况下，R² 可能小于零，这通常意味着模型的预测效果比简单地用均值预测还要差。

⑤ 总结

• OLS 是一种方法，用于估计线性回归模型的参数，目标是最小化残差平方和。
• RSS 是衡量模型预测准确性的一种指标，反映了实际观测值与预测值之间的差异。

在实践中，使用OLS方法来估计模型参数的过程实际上就是在计算RSS并寻找最小值的过程。因此，OLS和RSS在回归分析中是密切相关的，OLS通过最小化RSS来寻找最佳参数。

线性回归的目的是找到回归系数 ( ${\beta }_0$, ${\beta }_1$, $\dots$, ${\beta }_n$ )，使模型的预测值尽量与真实值接近。最终目的是让模型能够很好地概括数据，从而对未见过的数据进行准确的预测。

3. 线性回归的假设

在使用线性回归时，有几个基本假设条件：

1. 线性关系：目标变量和自变量之间存在线性关系。
2. 正态分布的误差项：残差（实际值与预测值之差）应该是正态分布的。
3. 独立误差：残差之间没有自相关性。
4. 同方差性：所有自变量的残差的方差是相同的，即残差的方差不随着自变量的变化而变化（即无异方差性问题）。
5. 自变量之间无多重共线性：多个自变量之间不应该高度相关。

4. 线性回归的类型

• 简单线性回归：仅有一个自变量的线性回归模型。

$$y={\beta }_0+{\beta }_1{x}_1+ϵ$$

• 多元线性回归：有多个自变量的线性回归模型。

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_n{x}_n+ϵ$$

5. 线性回归的代码示例

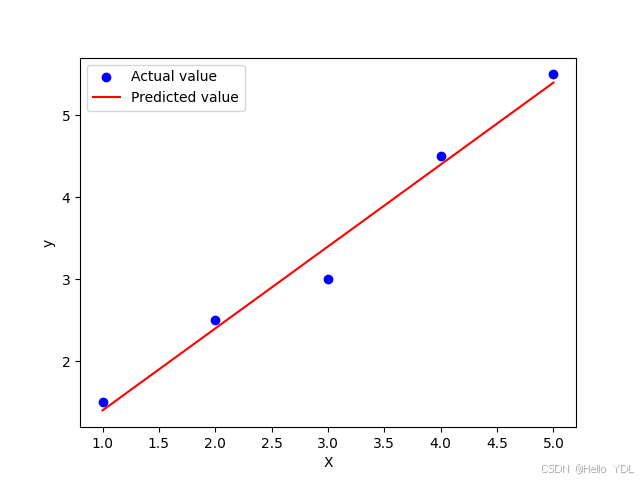
示例 1：简单线性回归

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 样本数据
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([1.5, 2.5, 3.0, 4.5, 5.5])

# 创建线性回归模型
model = LinearRegression()
model.fit(X, y)

# 打印系数和截距
print("系数:", model.coef_)
print("截距:", model.intercept_)

# 预测值
y_pred = model.predict(X)

# 绘图
plt.scatter(X, y, color="blue", label="实际值")
plt.plot(X, y_pred, color="red", label="预测值")
plt.xlabel("X")
plt.ylabel("y")
plt.legend()
plt.show()

解释：

• 用 LinearRegression().fit(X, y) 方法对样本数据进行拟合，获得模型的系数和截距。
• model.coef_ 返回回归系数，model.intercept_ 返回截距。
• 通过 model.predict(X) 进行预测，并将预测值和实际值绘制在同一图上。
  结果：
  
  

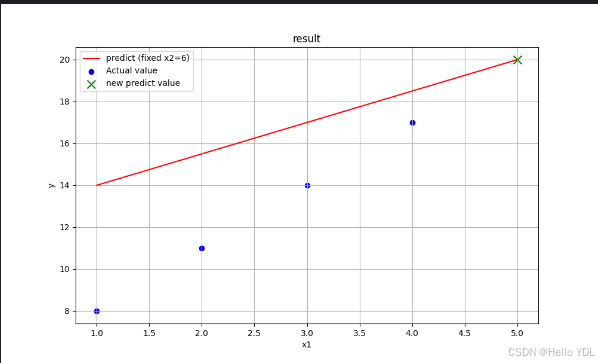
示例 2：多元线性回归

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 样本数据
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.dot(X, np.array([1, 2])) + 3  # y = 1*x1 + 2*x2 + 3

# 创建线性回归模型
model = LinearRegression()
model.fit(X, y)

# 打印系数和截距
print("系数:", model.coef_)
print("截距:", model.intercept_)

# 新数据的预测
new_data = np.array([[5, 6]])
prediction = model.predict(new_data)
print("Predicted value:", prediction)

# 绘图
x1_range = np.linspace(1, 5, 100)
fixed_x2 = 6  # 固定 x2 的值
predictions = model.predict(np.column_stack((x1_range, np.full(x1_range.shape, fixed_x2))))

plt.figure(figsize=(10, 6))
plt.plot(x1_range, predictions, color='red', label=f'predict (fixed x2={fixed_x2})')
plt.scatter(X[:, 0], y, color='blue', label='Actual value')
plt.scatter(new_data[0, 0], prediction, color='green', marker='x', s=100, label='new predict value')
plt.title('result')
plt.xlabel('x1')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()

解释：

• 这里我们创建了一个包含两个自变量的多元线性回归模型。
• 用 model.coef_ 查看回归系数，用 model.intercept_ 查看截距。
• 通过 model.predict 对新输入的数据进行预测。
  结果：
  

示例 3：带正则化的线性回归（岭回归）

import numpy as np
from sklearn.linear_model import Ridge

# 样本数据
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.dot(X, np.array([1, 2])) + 3

# 创建带正则化的线性回归模型
ridge_model = Ridge(alpha=1.0)
ridge_model.fit(X, y)

# 打印系数和截距
print("系数:", ridge_model.coef_)
print("截距:", ridge_model.intercept_)

解释：

• Ridge 是一种带有L2正则化的线性回归模型，它可以避免模型对多重共线性问题的敏感性。
• alpha 参数控制正则化的强度，值越大，正则化越强。

6. 线性回归的优点

• 简单易理解：线性回归模型结构简单，易于解释。模型中的系数可以解释每个自变量对因变量的贡献。
• 计算效率高：它的计算复杂度较低，适用于大规模数据集，尤其是在特征数较少时。
• 适用于线性关系：当目标变量和自变量之间的关系是线性时，线性回归效果非常好。
• 理论基础深厚：线性回归有成熟的理论基础，可以借助统计学方法解释。

7. 线性回归的缺点

• 假设过于严格：线性回归依赖于线性关系、同方差性、正态分布等假设，而在现实中这些假设常常无法满足。
• 对异常值敏感：线性回归对离群点（异常值）非常敏感，因为它通过最小化残差平方和来拟合模型，因此异常值可能会对模型造成较大影响。
• 无法处理复杂的非线性关系：如果目标变量与自变量之间的关系是非线性的，线性回归的表现就会不佳，模型无法捕捉到数据的复杂性。
• 多重共线性问题：当多个自变量之间高度相关时，回归系数可能会变得不稳定，影响模型的可靠性。
• 缺乏灵活性：线性回归不适合处理非线性数据，在某些复杂问题中表现欠佳。

8. 总结

线性回归是一种广泛应用的基础回归算法，适合用于自变量与因变量具有线性关系的数据集。它的优势在于易于实现和解释，计算复杂度低，适合处理大规模数据集。然而，线性回归的局限性在于其假设的严格性以及对异常值和多重共线性的敏感性。当面对复杂的非线性问题时，可以考虑其他更为灵活的回归方法或对模型进行扩展，比如多项式回归或正则化技术。

在实际应用中，选择线性回归模型时，应首先检查数据是否满足线性回归的基本假设，并根据实际情况调整模型或选择合适的回归技术。