代码地址:https://github.com/BosserWang/Multimodal-image-fusion
项目简介
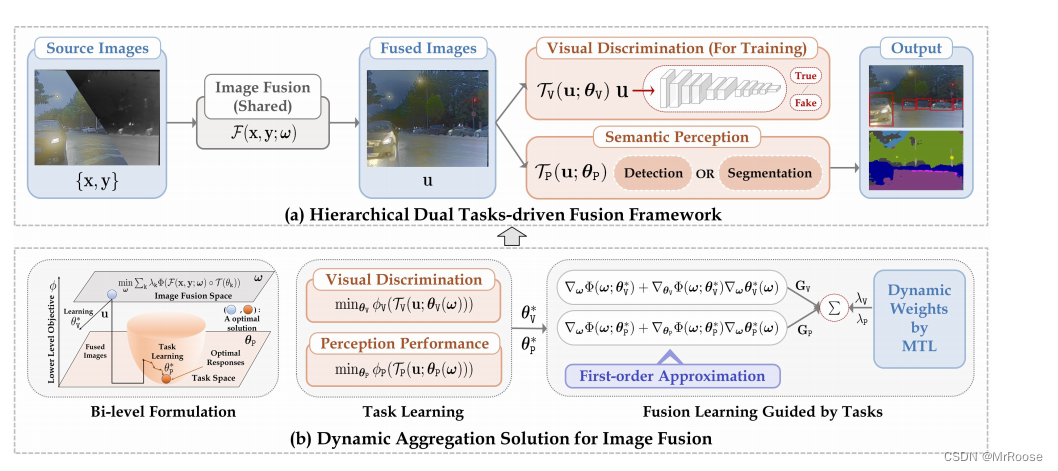
近年来,图像融合和场景理解等多模态场景感知任务在智能视觉系统中受到了广泛关注。然而,早期的努力总是考虑单方面推进某一项任务,而忽略其他任务,很少调查它们之间的潜在联系,以共同推进。为了克服这些限制,我们建立了分层双任务驱动的深度模型来桥接这些任务。具体而言,我们首先构建图像融合模块融合互补特征和级联双任务相关模块,包括视觉效果判别器和特征测量语义网络。我们提供了一个双层面的视角来制定图像融合和后续的下游任务。为了将不同的任务相关响应纳入图像融合,我们将图像融合作为主要目标,并将双模块作为可学习约束。此外,我们开发了一个有效的一阶近似来计算相应的梯度,并提出了动态加权聚合来平衡融合学习的梯度。大量的实验证明了我们的方法的优越性,它不仅产生了视觉上令人愉悦的融合结果,而且在检测和分割方面比目前最先进的方法有了显著的提升。
核心部分
为了方便大家直观了解本文的贡献,我直接先列出来了,方便大家阅读和思维碰撞。
- 图像融合模块为主要目标,下游的任务虽然是次要目标,但两者是相辅相成,互相促进,互相抑制(这一点可以参考下文中的损失函数)。
- 部分思想与对抗生成网络相似,本文我也用了判别器(Discriminator)来判断融合后的图片的纹理部分的差异化,建议阅读本文之前也先了解一下GAN。
- 融合的图像源是可见光图像和红外图像。
- 动态梯度聚合的目的是,为了自适应地平衡判别器和下游语义感知任务的梯度 G V \mathrm{G}_{\mathrm{V}} GV和 G P \mathrm{G}_{\mathrm{P}} GP,以共同优化融合网路 F \mathcal{F} F,通过使用RLW(随机损失加权) 根据正态分布来生成判别器的权重 λ V \lambda_{\mathrm{V}} λV和下游语义感知任务的权重 λ P \lambda_{\mathrm{P}} λP,以避免只关注一项任务而忽略另一项任务
- 为了求解 G V \mathrm{G}_{\mathrm{V}} GV和 G P \mathrm{G}_{\mathrm{P}} GP中的二阶梯度问题,受到了高斯-牛顿近似的启发,通过引入这个策略来近似梯度 G V \mathrm{G}_{\mathrm{V}} GV和 G P \mathrm{G}_{\mathrm{P}} GP中的海森矩阵,最后用一阶矢量来近似复杂的海森矩阵。
- 为了训练判别器,需要使用VSM构建伪融合图像,又采用了梯度惩罚机制 WGAN-GP,来保证学习的稳定性,解决了gan训练时容易出现的模型坍塌问题。
模型及方法
本模型可以分为图像融合模块
F
\mathcal{F}
F和下游任务模块
T
\mathcal{T}
T,因此整体网络模型可以通过
N
=
F
∘
T
\mathcal{N}=\mathcal{F}\circ\mathcal{T}
N=F∘T,通过不同损失函数的组合进行训练。我们认为现有的方法依赖于手工制作的视觉测量结果,这对于联合学习来说不具有适应性和灵活性。因此我们建立了分层双任务驱动的深度模型来桥接这些任务。具体来说,与图像融合一样,我们引入两个密集残差块来合成带有参数
w
\mathcal{w}
w的网络
F
\mathcal{F}
F,以保持源图像的互补特性,从而生成融合图像
u
\mathbf{u}
u。假设红外图像和可见光图像分别为具有灰度级的x和y,融合学习可写成
u
=
F
(
x
,
y
;
ω
)
\mathbf{u}={\mathcal{F}(\mathbf{x},\mathbf{y};\omega)}
u=F(x,y;ω) ,为了验证模型的自适应的能力,我们引入了一个参数是
θ
v
\theta_{\mathrm{v}}
θv的判别器
T
V
\mathcal{T}_{\mathrm{V}}
TV 来测量融合图像与源图像的纹理差异度。将分类输出表示为
z
V
\mathbf{z}_{\mathrm{V}}
zV,判别器整体表达式可以表述为:
z
V
=
T
V
(
u
;
θ
v
)
\mathbf{z}_{\mathrm{V}}={\mathcal{T}_{\mathrm{V}}(\mathbf{u};\theta_{\mathrm{v}})}
zV=TV(u;θv)。与手工制作的损失函数相比,这种表述方式可以提供自适应的可学习响应。
下游语义感知任务,选择物体检测和语义分割的两个代表性网络作为下游的语义感知模块
T
P
\mathcal{T}_{\mathrm{P}}
TP,参数为
θ
P
\theta_{\mathrm{P}}
θP。下游的语义感知模块整体表达式可以表述为:
z
P
=
T
P
(
u
;
θ
P
)
\mathbf{z}_{\mathrm{P}}={\mathcal{T}_{\mathrm{P}}(\mathbf{u};\theta_{\mathrm{P}})}
zP=TP(u;θP)。因此,完整的级联任务模块可以表述为:
u
=
F
(
x
,
y
;
ω
)
\mathbf{u}={\mathcal{F}(\mathbf{x},\mathbf{y};\omega)}
u=F(x,y;ω) ,
z
k
=
T
k
(
u
;
θ
k
)
\mathbf{z}_{\mathrm{k}}={\mathcal{T}_{\mathrm{k}}(\mathbf{u};\theta_{\mathrm{k}})}
zk=Tk(u;θk),
k
∈
{
V
,
P
}
\mathrm{k}\in\{\mathrm{V},\mathrm{P}\}
k∈{V,P},模型流程如图1(a)所示。与多任务学习相比,融合网络
F
\mathcal{F}
F实际上起到了稳健特征提取的作用(可视为 “编码器”)。
T
V
\mathcal{T}_{\mathrm{V}}
TV和
T
P
\mathcal{T}_{\mathrm{P}}
TP则作为特定任务的 “解码器”,用于学习辨别融合质量和衡量信息丰富度的能力,以支持下游场景感知。
双层任务驱动
针对高层次任务驱动的图像融合提出了多种训练策略,包括未滚动的端到端训练、单独的阶段性训练 和基于循环的自适应训练。然而我们发现,这些优化策略无法模拟视觉质量和语义重新解释之间的耦合互利关系,这不利于平衡不同任务的影响。因此,我们设计了新的学习范式,通过一个双层表述来描述整体优化过程。双层学习范式为:
min ω ∑ k λ k Φ k ( F ( x , y ; ω ) ∘ T k ( θ k ) ) , ( 2 ) \min_{\omega}\sum_{\mathrm{k}}\lambda_{\mathrm{k}}\Phi_{\mathrm{k}}(\mathcal{F}(\mathbf{x},\mathbf{y};\omega)\circ\mathcal{T}_{\mathrm{k}}(\theta_{\mathrm{k}})),\quad(2) minω∑kλkΦk(F(x,y;ω)∘Tk(θk)),(2)
s . t . { θ v ∗ = arg min θ v ϕ v ( T v ( u ; θ v ( ω ) ) ) , θ P ∗ = arg min θ p ϕ P ( T P ( u ; θ P ( ω ) ) ) , ( 3 ) \mathrm{s.t.} \begin{cases}\theta_{\mathrm{v}}^{*}=\arg\min_{\theta_{\mathrm{v}}}\phi_{\mathrm{v}}(\mathcal{T}_{\mathrm{v}}(\mathbf{u};\theta_{\mathrm{v}}(\omega))),\\\theta_{\mathrm{P}}^{*}=\arg\min_{\theta_{\mathrm{p}}}\phi_{\mathrm{P}}(\mathcal{T}_{\mathrm{P}}(\mathbf{u};\theta_{\mathrm{P}}(\omega))),\end{cases}\quad(3) s.t.{θv∗=argminθvϕv(Tv(u;θv(ω))),θP∗=argminθpϕP(TP(u;θP(ω))),(3)
其中 λ k \lambda_{\mathrm{k}} λk代表判别器和下游语义感知任务的动态权衡参数。(通过RLW实现)。具体来说,主要是优化融合网络 F \mathcal{F} F以提取丰富的特征,这对融合的质量和下游语义感知都有好处,如公式(2)所示。此外,图片融合效果的辨别和语义感知的理解反应是两个重要约束条件,如公式(3)所示。另一方面,公式 (2) 和公式 (3) 之间的分层表述是相互嵌套、相互促进的。融合图像 u \mathbf{u} u 是后续任务学习的基本数据依赖。后续任务学习的反馈又会促进图像融合的优化。
动态聚合
具体步骤如下:
- 需要多模态输入x, y,并有损失函数 ϕ V \phi_{\mathrm{V}} ϕV, ϕ P \phi_{\mathrm{P}} ϕP, Φ \Phi Φ,和其他超参数。
- 准备带有感知标签 z ∗ \mathbf{z}^{*} z∗的配对{x,y}。
- 启动 Warm start 策略
- 预训练融合网络 F \mathcal{F} F来初始化 w \mathcal{w} w。
- 对底层任务约束条件进行多步优化,估计出最优参数 θ V ∗ \theta_{\mathrm{V}}^* θV∗和 θ p ∗ \theta_{\mathrm{p}}^* θp∗
- 计算通过 θ V ∗ \theta_{\mathrm{V}}^* θV∗和 θ p ∗ \theta_{\mathrm{p}}^* θp∗得到 G V \mathbf{G}_\mathrm{V} GV和 G P \mathbf{G}_\mathrm{P} GP梯度。
- 使用RLW生成 λ V \lambda_{\mathrm{V}} λV和 λ P \lambda_{\mathrm{P}} λP。
- 通过公式 ω ← ω − ( λ V G V + λ P G P ) \omega\leftarrow\omega-({\lambda}_{\mathrm{V}}\mathbf{G}_{\mathrm{V}}+{\lambda}_{\mathrm{P}}\mathbf{G}_{\mathrm{P}}) ω←ω−(λVGV+λPGP)来更新 ω \omega ω。
- 判断是否到达收敛状态。
- 返回最终的 ω ∗ \omega^* ω∗和 θ p ∗ \theta_{\mathrm{p}}^* θp∗
简单来说,这个算法是在给定输入和损失函数的情况下,通过迭代更新网络权重,查找可使损失函数最小的权重的一种方法。明白了否?
动态聚合解决方案
min
ω
∑
k
λ
k
Φ
k
(
F
(
x
,
y
;
ω
)
∘
T
k
(
θ
k
)
)
,
(
2
)
\min_{\omega}\sum_{\mathrm{k}}\lambda_{\mathrm{k}}\Phi_{\mathrm{k}}(\mathcal{F}(\mathbf{x},\mathbf{y};\omega)\circ\mathcal{T}_{\mathrm{k}}(\theta_{\mathrm{k}})),\quad(2)
minω∑kλkΦk(F(x,y;ω)∘Tk(θk)),(2)
s
.
t
.
{
θ
v
∗
=
arg
min
θ
v
ϕ
v
(
T
v
(
u
;
θ
v
(
ω
)
)
)
,
θ
P
∗
=
arg
min
θ
p
ϕ
P
(
T
P
(
u
;
θ
P
(
ω
)
)
)
,
(
3
)
\mathrm{s.t.} \begin{cases}\theta_{\mathrm{v}}^{*}=\arg\min_{\theta_{\mathrm{v}}}\phi_{\mathrm{v}}(\mathcal{T}_{\mathrm{v}}(\mathbf{u};\theta_{\mathrm{v}}(\omega))),\\\theta_{\mathrm{P}}^{*}=\arg\min_{\theta_{\mathrm{p}}}\phi_{\mathrm{P}}(\mathcal{T}_{\mathrm{P}}(\mathbf{u};\theta_{\mathrm{P}}(\omega))),\end{cases}\quad(3)
s.t.{θv∗=argminθvϕv(Tv(u;θv(ω))),θP∗=argminθpϕP(TP(u;θP(ω))),(3)
我将详细地介绍是如何一步步解决上述的双层公式(2)、(3)。为了加快训练收敛速度,我们首先引入了预训练融合网络的 Warm start 策略。然后,我们提出了一种动态聚合解决方案,以共同解决融合和感知问题。具体的优化过程如图 2 (b) 所示。它实际上可以用分层优化来表示,即任务学习(公式 (3))和任务引导的融合学习(公式 (2))。按照现有的实用策略,我们首先对底层任务约束条件进行多步优化,以估计出最优参数 θ V ∗ \theta_{\mathrm{V}}^* θV∗和 θ p ∗ \theta_{\mathrm{p}}^* θp∗,从而学习基于特定任务损失的图像融合质量和下游语义感知任务的测量。考虑到融合任务与下级的任务之间的相互影响(用 θ k ( ω ) \theta_{\mathrm{k}}(\omega) θk(ω)来表示),分级任务之间实际上存在着复杂的联系,可以用来测量任务面对融合图像变化时的反应。通过对图像融合进行定时,可以得到双梯度,可写成:
{ G V = ∇ ω Φ V ( ω ; θ V ∗ ) + ∇ θ V Φ V ( ω ; θ V ∗ ) ∇ ω θ V ∗ ( ω ) , G P = ∇ ω Φ P ( ω ; θ P ∗ ) + ∇ θ P Φ P ( ω ; θ P ∗ ) ∇ ω θ V ∗ ( ω ) , ( 4 ) \left.\left\{\begin{matrix}\mathbf{G_{V}}=\nabla_{\omega}\Phi_{\mathrm{V}}(\omega;\theta_{\mathrm{V}}^{*})+\nabla_{\theta_{\mathrm{V}}}\Phi_{\mathrm{V}}(\omega;\theta_{\mathrm{V}}^{*})\nabla_{\omega}\theta_{\mathrm{V}}^{*}(\omega),\\\mathbf{G_{P}}=\nabla_{\omega}\Phi_{\mathrm{P}}(\omega;\theta_{\mathrm{P}}^{*})+\nabla_{\theta_{\mathrm{P}}}\Phi_{\mathrm{P}}(\omega;\theta_{\mathrm{P}}^{*})\nabla_{\omega}\theta_{\mathrm{V}}^{*}(\omega),\end{matrix}\right.\right.\quad(4) {GV=∇ωΦV(ω;θV∗)+∇θVΦV(ω;θV∗)∇ωθV∗(ω),GP=∇ωΦP(ω;θP∗)+∇θPΦP(ω;θP∗)∇ωθV∗(ω),(4)
具体来说,梯度 G V \mathbf{G}_\mathrm{V} GV和 G P \mathbf{G}_\mathrm{P} GP的计算公式为 Φ k ( F ( x , y ; ω ) ∘ T k ( θ k ) ) ) \Phi_{\mathbf{k}}(\mathcal{F}(\mathbf{x},\mathbf{y};\omega)\circ\mathcal{T}_{\mathbf{k}}(\theta_{\mathbf{k}}))) Φk(F(x,y;ω)∘Tk(θk))) 。公式(4)中的第一项 ∇ ω Φ V ( ω ; θ V ∗ ) \nabla_{\omega}\Phi_{\mathrm{V}}(\omega;\theta_{\mathrm{V}}^{*}) ∇ωΦV(ω;θV∗) 和 ∇ ω Φ P ( ω ; θ P ∗ ) \nabla_{\omega}\Phi_{\mathrm{P}}(\omega;\theta_{\mathrm{P}}^{*}) ∇ωΦP(ω;θP∗) 均是以 ω \omega ω 为单位的直接梯度,第二项 ∇ θ v Φ v ( ω ; θ v ∗ ) ∇ ω θ v ∗ ( ω ) \nabla_{\theta_\mathbf{v}}\Phi_\mathbf{v}(\omega;\theta_\mathbf{v}^*)\nabla_\omega\theta_\mathbf{v}^*(\omega) ∇θvΦv(ω;θv∗)∇ωθv∗(ω) 和 ∇ θ P Φ P ( ω ; θ P ∗ ) ∇ ω θ V ∗ ( ω ) \nabla_{\theta_{\mathrm{P}}}\Phi_{\mathrm{P}}(\omega;\theta_{\mathrm{P}}^{*})\nabla_{\omega}\theta_{\mathrm{V}}^{*}(\omega) ∇θPΦP(ω;θP∗)∇ωθV∗(ω) 描述了与下游任务的潜在耦合联系。
一阶近似
{ G V = ∇ ω Φ V ( ω ; θ V ∗ ) + ∇ θ V Φ V ( ω ; θ V ∗ ) ∇ ω θ V ∗ ( ω ) , G P = ∇ ω Φ P ( ω ; θ P ∗ ) + ∇ θ P Φ P ( ω ; θ P ∗ ) ∇ ω θ V ∗ ( ω ) , ( 4 ) \left.\left\{\begin{matrix}\mathbf{G_{V}}=\nabla_{\omega}\Phi_{\mathrm{V}}(\omega;\theta_{\mathrm{V}}^{*})+\nabla_{\theta_{\mathrm{V}}}\Phi_{\mathrm{V}}(\omega;\theta_{\mathrm{V}}^{*})\nabla_{\omega}\theta_{\mathrm{V}}^{*}(\omega),\\\mathbf{G_{P}}=\nabla_{\omega}\Phi_{\mathrm{P}}(\omega;\theta_{\mathrm{P}}^{*})+\nabla_{\theta_{\mathrm{P}}}\Phi_{\mathrm{P}}(\omega;\theta_{\mathrm{P}}^{*})\nabla_{\omega}\theta_{\mathrm{V}}^{*}(\omega),\end{matrix}\right.\right.\quad(4) {GV=∇ωΦV(ω;θV∗)+∇θVΦV(ω;θV∗)∇ωθV∗(ω),GP=∇ωΦP(ω;θP∗)+∇θPΦP(ω;θP∗)∇ωθV∗(ω),(4)
求解公式(4)是比较有挑战性的,尤其是第二项,需要计算二阶梯度。受到了高斯-牛顿近似的启发,我们引入了这一策略来近似梯度 G V \mathbf{G}_\mathrm{V} GV和 G P \mathbf{G}_\mathrm{P} GP 中的海森矩阵,高斯-牛顿近似提供了一阶计算来解决该问题。根据隐函数理论,我们可以得出 ∇ ω θ ( ω ) = − ∇ ω , θ 2 Φ ( ω ; θ ) ∇ θ , θ 2 Φ ( ω ; θ ) − 1 \nabla_{\omega}\theta(\omega)_{=} -\nabla_{\omega,\theta}^{2}\Phi(\omega;\theta)\nabla_{\theta,\theta}^{2}\Phi(\omega;\theta)^{-1} ∇ωθ(ω)=−∇ω,θ2Φ(ω;θ)∇θ,θ2Φ(ω;θ)−1 高斯-牛顿近似法可以用一阶矢量的产生来掩盖复杂的海森矩阵,即 ∇ ω θ ( ω ) ≈ ∇ θ Φ ( ω ; θ ) ⊤ ∇ θ ϕ ω ( ω ; θ ) ∇ θ ϕ ( ω ; θ ) ⊤ ∇ θ ϕ ( ω ; θ ) ∇ ω ϕ ( ω ; θ ) \nabla_\omega\theta(\omega)\approx\frac{\nabla_\theta\Phi(\omega;\theta)^\top\nabla_\theta\phi\omega(\omega;\theta)}{\nabla_\theta\phi(\omega;\theta)^\top\nabla_\theta\phi(\omega;\theta)}\nabla_\omega\phi(\omega;\theta) ∇ωθ(ω)≈∇θϕ(ω;θ)⊤∇θϕ(ω;θ)∇θΦ(ω;θ)⊤∇θϕω(ω;θ)∇ωϕ(ω;θ)
动态梯度聚合
另一个具有挑战性的问题是如何自适应地平衡梯度 G V \mathbf{G}_\mathrm{V} GV和 G P \mathbf{G}_\mathrm{P} GP ,以共同优化图像融合网络 F \mathcal{F} F。最近,随机损失加权(RLW)在多任务学习(MTL)中得到了推广,它可以避免局部最小值,具有更高的泛化能力和可比性能。我们利用正态分布 p( λ \lambda λ) 来生成 λ V \lambda_{\mathrm{V}} λV和 λ P \lambda_{\mathrm{P}} λP,以避免只关注一项任务而忽略另一项任务。
损失函数
我将分别阐述定义 ϕ \phi ϕ, Φ \Phi Φ的具体损失函数,它们可分图像融合质量和语义感知两部分。至于判别器 T v \mathcal{T}_{\mathrm{v}} Tv 的学习,我们引入了生成对抗机制来判别图像融合的视觉质量。具体来说,我们首先利用 VSM 构建伪融合图像(mask) u m \mathbf{u}_m um,通过显著性权重图(m1 和 m2)保持显著性信息,即 u m = m 1 x + m 2 y \mathbf{u}_m=\mathfrak{m}_1\mathbf{x}+\mathfrak{m}_2\mathbf{y} um=m1x+m2y。我们还采用梯度惩罚WGAN-GP来保证学习的稳定性,因此训练 T v \mathcal{T}_{\mathrm{v}} Tv 的具体公式可以写为
ϕ v = E s ~ ∼ P f a k e T V ( u ) − E s ∼ P r e a l T V ( u m ) + η R P e n a l t y , ( 6 ) \phi_{\mathrm{v}}=\mathbb{E}_{\tilde{\mathbf{s}}\sim\mathbb{P}_{\mathrm{fake}}}\mathcal{T}_{\mathrm{V}}(\mathbf{u})-\mathbb{E}_{\mathbf{s}\sim\mathbb{P}_{\mathrm{real}}}\mathcal{T}_{\mathrm{V}}(\mathbf{u}_{m})+\eta\mathbb{R}_{\mathrm{Penalty}},\quad(6) ϕv=Es~∼PfakeTV(u)−Es∼PrealTV(um)+ηRPenalty,(6)
其中,
R
P
e
n
a
l
t
y
\mathbb{R}_{\mathrm{Penalty}}
RPenalty是惩罚项,由
E
s
~
∼
P
f
a
k
e
[
(
∥
∇
u
T
V
(
u
)
∥
2
−
1
)
2
]
\mathbb{E}_{\tilde{\mathbf{s}}\sim\mathbb{P}_{\mathbf{fake}}}[(\|\nabla_{\mathbf{u}}{\mathcal{T}_{\mathbf{V}}}(\mathbf{u})\|_{2}-1)^{{2}}]
Es~∼Pfake[(∥∇uTV(u)∥2−1)2] 计算得出,
η
\eta
η 是权衡项。此外,图像融合网络
F
\mathcal{F}
F 可视为生成器。为了平衡像素强度和避免纹理伪影,我们还利用像素误差损失进行融合学习,即
Φ
v
=
∥
u
−
m
1
x
∥
2
2
+
∥
u
−
m
2
y
∥
2
2
−
E
s
∼
P
r
e
a
1
T
V
(
u
)
.
(
7
)
\Phi_{\mathrm{v}}=\|\mathbf{u}-\mathbf{m}_{1}\mathbf{x}\|_{2}^{2}+\|\mathbf{u}-\mathbf{m}_{2}\mathbf{y}\|_{2}^{2}-\mathbb{E}_{\mathbf{s}\sim\mathbb{P}_{\mathbf{rea}1}}\mathcal{T}_{\mathrm{V}}(\mathbf{u}).\quad(7)
Φv=∥u−m1x∥22+∥u−m2y∥22−Es∼Prea1TV(u).(7)
至于 T P \mathcal{T}_{\mathrm{P}} TP 的语义感知优化,我们采用常见的特定任务损失函数来训练感知相关目标(即 Φ P \Phi_{\mathrm{P}} ΦP, ϕ P \phi_{\mathrm{P}} ϕP)。对于物体检测,我们利用 FCOS的混合损失函数来定义目标。至于语义分割,我们使用了交叉熵损失函数。
效果展示
左图为可见光图像,右图为红外图像
左图为检测效果图,右图为图像融合效果图