完成了我们的专题1——树 部分的刷题练习之后 我们(终于!)来到了第二部分:数组与字符串
经历了专题1大量题目洗礼过后的我们 应该变得对刷题更有自信了!(没看过专题1的内容不妨回去看一眼~)那么 我们继续!
【1】先对
LeetBook中的内容进行一个学习
数组是数据结构中的基本模块之一。- 因为
字符串是由字符数组形成的,所以二者是相似的。
——我们面临的大多数面试问题都属于这个范畴。要刷的题目涉及如下专题——
(1)专题1 理解数组的基本概念及其操作方式;
(2)专题2 理解二维数组的基本概念,熟悉二维数组的使用;
(3)专题3 了解字符串的概念以及字符串所具有的不同特性;理解字符串匹配中的KMP 算法;
(4)专题4 能够运用双指针解决实际问题。
【2】在解决
LeetBook中推荐的题目的过程中 我发现了非常有趣的两个专题——
(1)专题5 前缀和思想求解子数组&子串问题
(2)专题6 二分查找数组中元素问题
文章目录
本专题有三道题
都是需要通过一定的数学知识 找到规律 然后利用循环解题!
[2]二维数组简介
多维数组适合像表/矩阵这样更复杂的结构
本章中我们围绕二维数组解释——
- 二维数组在内存中是如何存放的
- 如何运用二维数组来解决问题
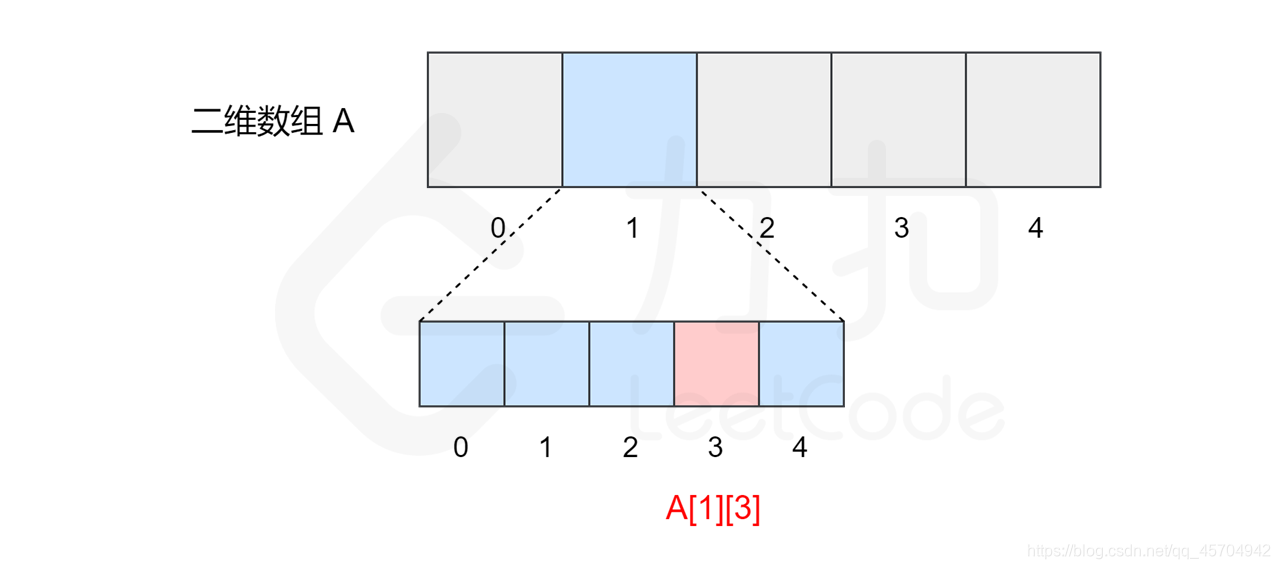
二维数组是一种结构较为特殊的数组,只是将数组中的每个元素变成了一维数组。
所以二维数组的本质上仍然是一个一位数组
另外 其内部的一位数组仍然从索引0开始
我们可以将它看作一个矩阵 并处理矩阵的相关问题
示例
类似一维数组,对于一个二维数组 A = [[1, 2, 3, 4],[2, 4, 5, 6],[1, 4, 6, 8]]
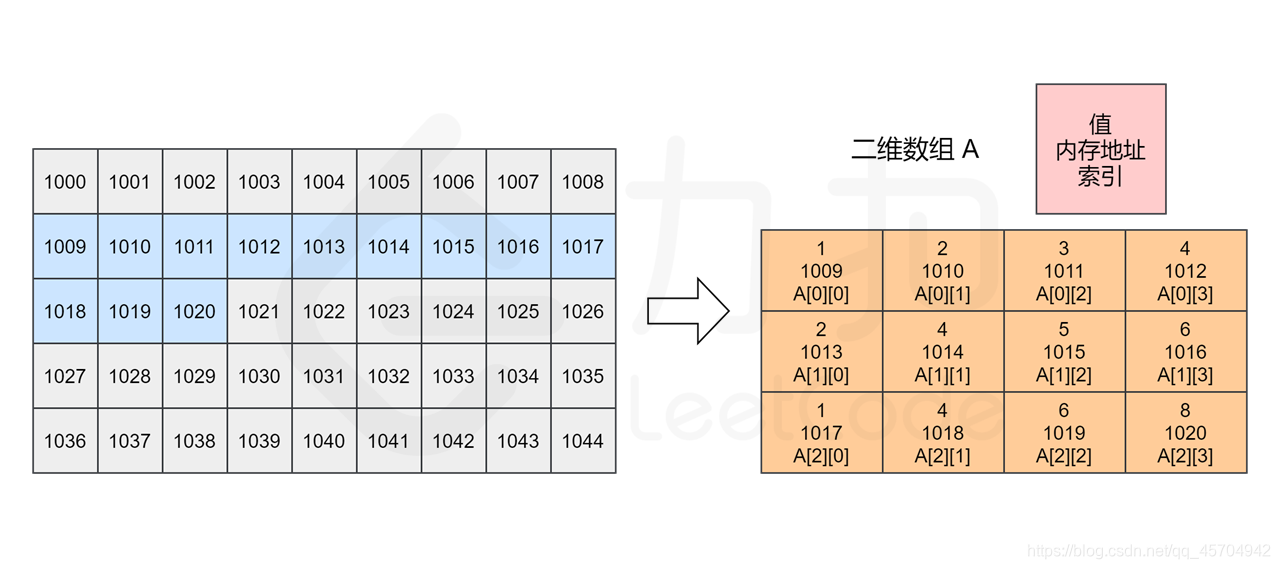
计算机同样会在内存中申请一段 连续 的空间,并记录第一行数组的索引位置 即 A[0][0] 的内存地址
它的索引与内存地址的关系如下图所示——
注意 实际数组中的元素由于类型的不同 会占用不同的的字节数 因此每个方格地址之间的差值可能不为1
实际题目中 往往使用二维数组处理矩阵类相关问题
包括矩阵旋转 对角线遍历 以及对子矩阵的操作等
做三道题练习一下二维数组 都是围绕着矩阵来玩儿~
面试题 01.07. 旋转矩阵 medium
本题与主站 48 题 旋转图像相同:
给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
解题思路
【1】使用 辅助数组 这个应该就是easy级别的做法了
诶就很简单
需要注意的是
题目的输入是一个数组 最后返回的也是这个数组
所以最后需要把辅助数组的内容全部赋给输入的数组(这个一开始没注意到 结果一跑结果发现 诶 为啥没变化)
复杂度分析
- 时间复杂度:O(N2),其中 N 是 matrix的边长。
- 空间复杂度:O(N2),我们需要使用一个和 matrix 大小相同的辅助数组。
【2】原地旋转 medium级别的高级
以下方法都参考了官方题解辽
想不出来不用辅助数组的方法嘤嘤嘤
详情康官方题解吧~这里就不复现了
【3】用翻转代替旋转 medium级别的更好想的做法
(但还是好难想呐!小声bb)
步骤为:
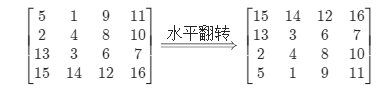
【1】先根据水平轴翻转
【2】再根据主对角线翻转
为啥?
因为经过这两步操作之后 发现得到了一个很眼熟的公式
做题的时候把图画出来 会更好想哦~
注意对角线翻转的写法 第一次就很智障地写错了。跑完发现结果和水平翻转完恰好一样 才发现给的测试用例恰好就满足这么个情况…
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){
//注意是i嗷
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
- 时间复杂度:O(N2),其中 N 是 matrix的边长。对于每一次翻转操作 我们都需要枚举矩阵中一半的元素
- 空间复杂度:O(1),为原地翻转得到的原地旋转。
Java代码
【1】辅助数组法
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
int[][] matrix_new = new int [n][n];//初始化二维数组(有数组长度的情况下)
for(int i = 0; i < matrix.length; i++)