在颓废了一段时间后，我内心是自责不安~~，决定重新踏上量子机器学习的康庄大道，由于近期学习的一篇论文里面涉及到一些机器学习算法，为了能将论文顺利看懂，“被逼”学习LDA，这也算是比较高阶的机器学习算法了，之前也从未接触过，下面做出详解！

一 . LDA简介

之前的博客学习中，我们接触过PCA主成分分析法，它是一种常见的数据降维算法，而本次我们重点介绍的LDA在某种程度上和PCA有着异曲同工之妙：线性判别分析（LDA）最常在模式分类和机器学习应用的预处理步骤中用作降维技术。目的是将数据集投影到具有良好类可分离性的低维空间上，以避免过度拟合（“维数的诅咒”）并降低计算成本。

因此，简而言之，LDA的目标通常是将特征空间（数据集的n维样本）投影到较小的子空间 $k(k<n-1)$ 上，同时保留类别歧视信息。

什么是良好的特征子空间？

毫无疑问，我们的目标是缩小$d$ 维数据，将其投影到 $k$ 维子空间上，其中 $k<d$。那么。如何判断这个新映射的子特征空间能够很好的表示原先的数据呢？

与传统的图像数据处理利用特征值和特征向量相似，这次是将原始数据中的特征向量（分量）收集到一个所谓的分散矩阵中，也就是后面将会提到的类间分散矩阵和类内分散矩阵）。

由于每个特征值都对应其特征向量，如果观察到所有的特征值都有相似的大小，那么，这就在间接的告诉我们：此时原始数据已经投射到了一个好的特征空间上。

如果映射子空间后得到的特征值大小分布并不均衡，有些特征值大于，甚至是远大于其他的特征值，此时，我们应该果断留下那些对应着特征值较大的特征向量，因为他们包含着更多的关键信息和有用数据，其余的特征向量可以直接去除，这里的思想和奇异值分解处理模糊图像的方法不能说是毫无关系，简直是一模一样！！！

LDA思想
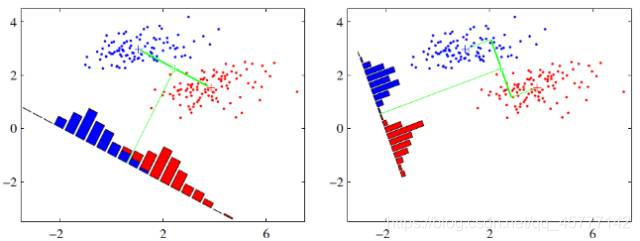
LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。它的主要思想可以用一句话概括，就是 “投影后类内方差最小，类间方差最大” ，如下图所示。 我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大

还说看图说话，变抽象为具象：

假设有两类数据，分别为红色和蓝色，如上图所示，这些数据特征是二维的，希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大，显然，上图右边的结果更符合LDA的核心思想！

二 . 算法推导

算法的主要推导对象是数据的映射方向！

由于公式的复杂性，这里采用二维空间中的两类样本为例，也符合上图，根据前面 “投影后类内方差最小，类间方差最大” 的主要思想我们做出如下推导：

假设有一个数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) ⋯ ( x m , y m ) } D = \left \{ (x_{1},y_{1}),(x_{2},y_{2})\cdots (x_{m},y_{m})\right \} D={(x1​,y1​),(x2​,y2​)⋯(xm​,ym​)}，其中，任意样本 $x_i$ 为 $n$ 维向量，且定义 $N_j$ 为 第 $j$ 类样本的个数，$X_j$ 为第 $j$ 类 样本的合集，而 ${\mu }_j$ 为 第 $j$ 类样本的均值向量，${\Sigma }_j$为样本的 方差，且这里的 $j$ 为 $1$ 和 $2$,也就是数据集中的 $x$ 样本和 $y$ 样本。

因此，两类的均值向量为:
$${\mu }_i=\frac{1}{N_i}\sum _{x\in {\omega }_i}x$$
同时保证让投影之后的中心距离尽可能的大，也就是:
$$\mathrm{J}(\mathrm{w})=\left|\widetilde{{\mu }_1}-\widetilde{{\mu }_2}\right|=\left|w^T\left({\mu }_1-{\mu }_2\right)\right|$$
其中，
$${\tilde{\mu }}_i=\frac{1}{N_i}\sum _{y\in {\omega }_i}y=\frac{1}{N_i}\sum _{x\in {\omega }_i}{w}^{T}x=w^T{\mu }_i$$是来自类别 $i$ 的投影数据的均值 , $w^T$ 是投影向量。但是，通过增大$w$，这个表达式可以任意增大。为了解决这个问题，我们可以将$w$限制为单位长度，即${\sum }_i{w}_i^2=1$ 。
至此，投影的建立已经算是完成了，接下来需要做的就是最小化类内的方差，接着上面的推导，投影结束之后，假设样本的坐标为 $y$， 投影也就是 $y={\mathbf{w}}^T\mathbf{x}$ , 那么投影后的方差就是：
$${\tilde{s}}_i^2=\sum _{y\in {\omega }_i}{\left(y-{\tilde{\mu }}_i\right)}^2$$

所以两个样本的方差相加为 ${\tilde{s}}_2^1+{\tilde{s}}_2^2$ ，再根据 “投影后类内方差最小，类间方差最大” 的原则，我们需要最大化：
$$\mathrm{J}(\mathrm{w})=\frac{{\left|\widetilde{{\mu }_1}-\widetilde{{\mu }_2}\right|}^2}{{\tilde{\mathrm{s}}}_1^2+{\tilde{\mathrm{s}}}_2^2}$$

现在我们需要改写这个式子，使得能让我们在数学层面上有方法最大化它，因为$\widetilde{{\mu }_k}={\mathbf{w}}^T{\mu }_k$，$y={\mathbf{w}}^T\mathbf{x}$,分子改写为：
$${\left({\tilde{\mu }}_1-{\tilde{\mu }}_2\right)}^2={\left(w^{\top }{\mu }_1-w^{\top }{\mu }_2\right)}^2=w^{\top }\left({\mu }_1-{\mu }_2\right){\left({\mu }_1-{\mu }_2\right)}^{\top }w=w^{\top }{S}_{B}W$$

分母中的每一项课改写为：
$${\tilde{s}}_i^2=\sum _{y\in {\omega }_i}{\left(y-{\tilde{\mu }}_i\right)}^2=\sum _{x\in {\omega }_i}{\left(w^{T}x-w^T{\mu }_i\right)}^2=\sum _{x\in {\omega }_i}{w}^T\left(x-{\mu }_i\right){\left(x-{\mu }_i\right)}^{T}w$$

最终化简为：
$$J(\mathbf{w})=\frac{{\mathbf{w}}^T{\mathbf{S}}_B\mathbf{w}}{{\mathbf{w}}^T{\mathbf{S}}_W\mathbf{w}}$$

其中，矩阵${\mathbf{S}}_B$ 和${\mathbf{S}}_W$ 就是我们开头说的类间散度矩阵和类内散度矩阵 ，求极值的通法都是求导，现直接对$J(\mathbf{w})$ 关于$w$求导，令之为0，得到取到极值的条件为：
$$\left({\mathbf{w}}^T{\mathbf{S}}_B\mathbf{w}\right){\mathbf{S}}_W\mathbf{w}=\left({\mathbf{w}}^T{\mathbf{S}}_W\mathbf{w}\right){\mathbf{S}}_B\mathbf{w}$$
由于$\left(w^T{S}_{B}w\right)$ 和 $\left(w^T{S}_{W}w\right)$是标量，可得：
$$S_{B}w=\lambda S_{W}w$$
同时左乘$S_W^{-1}$ 得：
$$S_W^{-1}{S}_{B}w=\lambda w$$

显然，这个就是特征方程了，终于到达了前面说的特征值和特征向量！

再回到前面推导时候说过：$S_B=\left({\mu }_1-{\mu }_2\right){\left({\mu }_1-{\mu }_2\right)}^T$，所以$S_{B}w$的方向就是$\left({\mu }_2-{\mu }_1\right)$，可用$\lambda \left({\mu }_2-{\mu }_1\right)$ 来代替。再结合前面的额特征方程，我们可以得到：
$$w\propto S_W^{-1}\left(\widetilde{{\mu }_2}-\widetilde{{\mu }_1}\right)$$

最后，我们恍然大悟，只需要求出原始样本的均值和方差就可以求出最佳的方向 $w$

总的来说，推导过程的理解还是不难的，只需要线性代数的简单基础就行了，没有什么高级的地方。

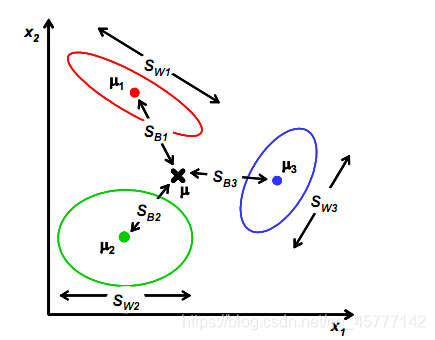
那么回过头来，上述推导是建立在二维数据降到一维的情况，那真的做项目的时候可能就没那么顺利了，有可能是多维数据，要下降几个维度，但是基本上还是换汤不换药，方法类似，通过下面这个图也能非常清晰的看出高阶数据的LDA方法：

三 . 小项目练习

从上文中我们可以总结出，LDA降维一般分为5个步骤：

1. 计算数据集中每个类别样本的均值向量。
2. 通过均值向量，计算类间散度矩阵$S_B$和类内散度矩阵 $S_w$ 。
3. 对$S_W^{-1}{S}_{B}W=\lambda W$，进行特征值求解， 求出$S_W^{-1}{S}_B$的特征向量和特征值。
4. 对特征向量按照特征值的大小降序排列，并选择前K个特征向量组成投影矩阵$W$。
5. 通过$D\times K$维的特征值矩阵将样本点投影到新的子空间中，$Y=X\cdot W$。

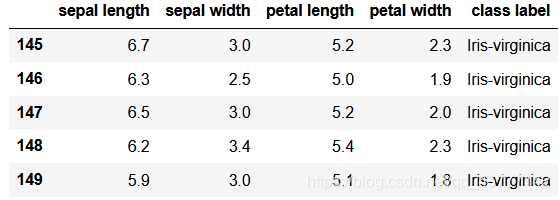
本次使用传统的鸢尾花数据集进行试验，因为该数据集有很多的类，方便我们降维，其中包含萼片长度、萼片宽度、花瓣长度、花瓣宽度四个关键类，单位都是cm，除此之外，本数据集中，有三种不同种类的鸢尾花，他们分别是$Iris-setosa$ 、$Iris-versicolor$、$Iris-virginica$。

我们首先导入数据，并展示最后五行数据的大致情况：

import pandas as pd
df = pd.read_csv('iris.data', header=None)

feature_dict = {i:label for i,label in zip(
                range(4),
                  ('sepal length',
                  'sepal width',
                  'petal length',
                  'petal width', ))}
df.columns = [l for i,l in sorted(feature_dict.items())] + ['class label']
df.dropna(how="all", inplace=True) 
df.tail()

为了面处理的方便，我们将其全部转变为数字，不留文本格式。

from sklearn.preprocessing import LabelEncoder
X = df[['sepal length in cm', 'sepal width in cm', 'petal length in cm', 'petal width in cm']].values
y = df['class label'].values
enc = LabelEncoder()
label_encoder = enc.fit(y)
y = label_encoder.transform(y) + 1
label_dict = {1: 'Setosa', 2: 'Versicolor', 3:'Virginica'}

上面代码将前面行列的文本全部标签化了，下面我们画出各个种类的柱状图：

import math
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(12,6))

for ax,cnt in zip(axes.ravel(), range(4)):  

    # set bin sizes
    min_b = math.floor(np.min(X[:,cnt]))
    max_b = math.ceil(np.max(X[:,cnt]))
    bins = np.linspace(min_b, max_b, 25)

    # plottling the histograms
    for lab,col in zip(range(1,4), ('blue', 'red', 'green')):
        ax.hist(X[y==lab, cnt],
                   color=col,
                   label='class %s' %label_dict[lab],
                   bins=bins,
                   alpha=0.5,)
    ylims = ax.get_ylim()

    # plot annotation
    leg = ax.legend(loc='upper right', fancybox=True, fontsize=8)
    leg.get_frame().set_alpha(0.5)
    ax.set_ylim([0, max(ylims)+2])
    ax.set_xlabel(feature_dict[cnt])
    ax.set_title('Iris histogram #%s' %str(cnt+1))

    # hide axis ticks
    ax.tick_params(axis="both", which="both", bottom="off", top="off",  
            labelbottom="on", left="off", right="off", labelleft="on")

    # remove axis spines
    ax.spines["top"].set_visible(False)  
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)    

axes[0][0].set_ylabel('count')
axes[1][0].set_ylabel('count')

fig.tight_layout()       

plt.show()

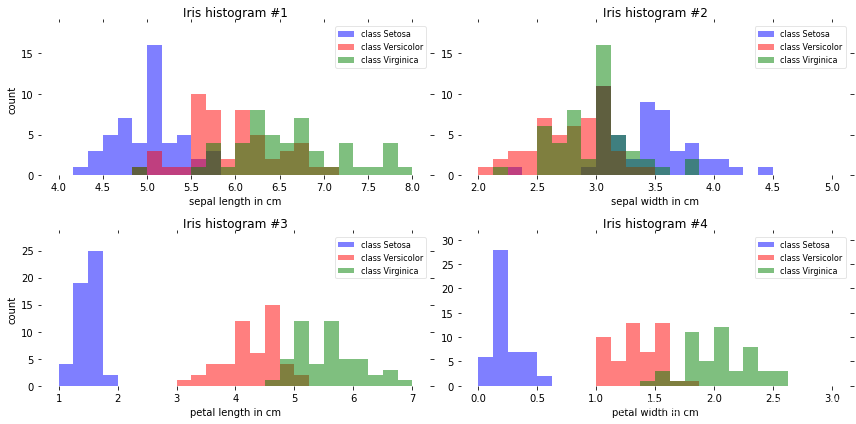
分别得到鸢尾花中四个参数(萼片长度、宽度，花瓣长度、宽度)下，三个不同种类鸢尾花的柱状图。

显然，四幅图中上方两幅区分性不强，而下面代表花瓣宽度和长度的数据区分度比较大，因为这2个特征的直方图中，不同的类别的样本较为分散！

下一步就需要计算特征样本的均值和方差了，由于纯数学问题，就直接上代码了：

np.set_printoptions(precision=4)

mean_vectors = []
for cl in range(1,4):
    mean_vectors.append(np.mean(X[y==cl], axis=0))
    print('Mean Vector class %s: %s\n' %(cl, mean_vectors[cl-1]))

接下来，根据前面的介绍，关键的类内散度矩阵和类间散度矩阵就来了：

#类内散度矩阵：Sw
S_W = np.zeros((4,4))
for cl,mv in zip(range(1,4), mean_vectors):
    class_sc_mat = np.zeros((4,4))                  # scatter matrix for every class
    for row in X[y == cl]:
        row, mv = row.reshape(4,1), mv.reshape(4,1) # make column vectors
        class_sc_mat += (row-mv).dot((row-mv).T)
    S_W += class_sc_mat                             # sum class scatter matrices
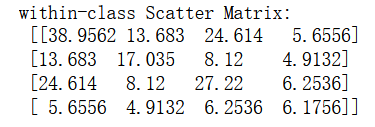
print('within-class Scatter Matrix:\n', S_W)

# 类间散度矩阵:Sb
overall_mean = np.mean(X, axis=0)
S_B = np.zeros((4,4))
for i,mean_vec in enumerate(mean_vectors):  
    n = X[y==i+1,:].shape[0]
    mean_vec = mean_vec.reshape(4,1) # make column vector
    overall_mean = overall_mean.reshape(4,1) # make column vector
    S_B += n * (mean_vec - overall_mean).dot((mean_vec - overall_mean).T)
print('between-class Scatter Matrix:\n', S_B)

结果分别为：

然后，就是$S_W^{-1}{S}_B$的特征方程求解了：

eig_vals, eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))

for i in range(len(eig_vals)):
    eigvec_sc = eig_vecs[:,i].reshape(4,1)   
    print('\nEigenvector {}: \n{}'.format(i+1, eigvec_sc.real))
    print('Eigenvalue {:}: {:.2e}'.format(i+1, eig_vals[i].real))

此时，我们就可以确定投影方向了，也就能选择新的特征空间了：

# Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)
# Visually confirm that the list is correctly sorted by decreasing eigenvalues
print('Eigenvalues in decreasing order:\n')
for i in eig_pairs:
    print (i[0], i[1])

先将特征向量按照特征值的大小降序排列，老板的线代告诉我：特征向量和特征值代表了变换后的方向以及该方向上的缩放比例，因此特征值越大，说明这个方向在变换中越显著，也就是信息量最大，同时抛弃特征值较小的方向，我们只需要选取前k个特征值对应的特征向量，就得到了映射矩阵W：

显然，上图中，只有第一列是特征值，有两个值以及无限接近0了。我们映射的有用特征值只有2个！

# 我们通过特征值的比例来体现方差的分布：
print('Variance explained:\n')
eigv_sum = sum(eig_vals)
for i,j in enumerate(eig_pairs):
    print('eigenvalue {0:}: {1:.2%}'.format(i+1, (j[0]/eigv_sum).real))

注意，这里我们只取前两个！

# 选择K个特征向量作为映射矩阵，这里选了前2个有信息的。
W = np.hstack((eig_pairs[0][1].reshape(4,1), eig_pairs[1][1].reshape(4,1)))
print('Matrix W:\n', W.real)

就快结束了，我们现在唯一需要做的收尾工作就是将样本投影到新的空间

X_lda = X.dot(W)
assert X_lda.shape == (150,2), "The matrix is not 150x2 dimensional."

def plot_step_lda():

    ax = plt.subplot(111)
    for label,marker,color in zip(
        range(1,4),('^', 's', 'o'),('blue', 'red', 'green')):

        plt.scatter(x=X_lda[:,0].real[y == label],
                y=X_lda[:,1].real[y == label],
                marker=marker,
                color=color,
                alpha=0.5,
                label=label_dict[label]
                )

    plt.xlabel('LD1')
    plt.ylabel('LD2')

    leg = plt.legend(loc='upper right', fancybox=True)
    leg.get_frame().set_alpha(0.5)
    plt.title('LDA: Iris projection onto the first 2 linear discriminants')

    # hide axis ticks
    plt.tick_params(axis="both", which="both", bottom="off", top="off",  
            labelbottom="on", left="off", right="off", labelleft="on")

    # remove axis spines
    ax.spines["top"].set_visible(False)  
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)    

    plt.grid()
    plt.tight_layout
    plt.show()

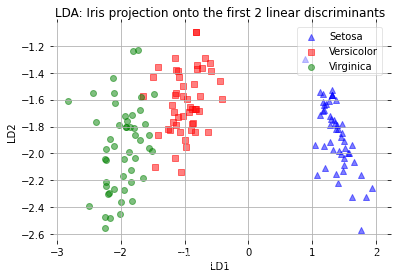
plot_step_lda()

从上面这个散点图中，我们可以看出，第一个线性判别LD1可以很好地将类别区分开来，但是第二个线性判别LD2，由于不含有充分的信息（可以从之前的特征向量中看出）。并没有很好的区分性。原先需要四个图表示的多维向量数据，在这里，用一个二维散点图就可以了！