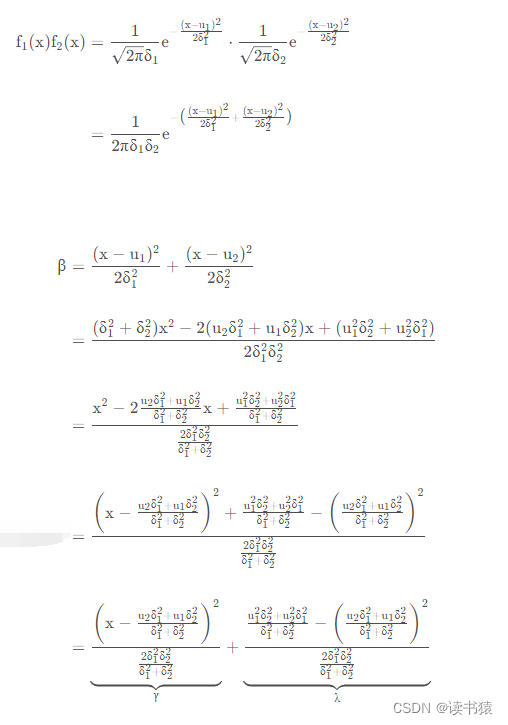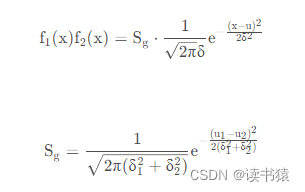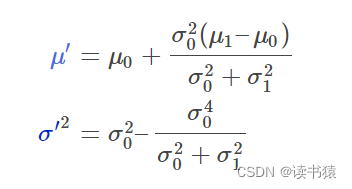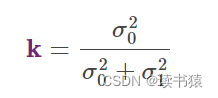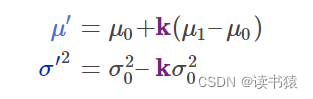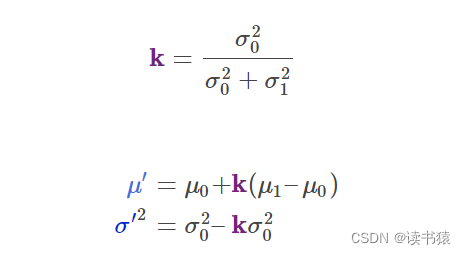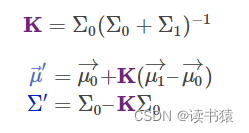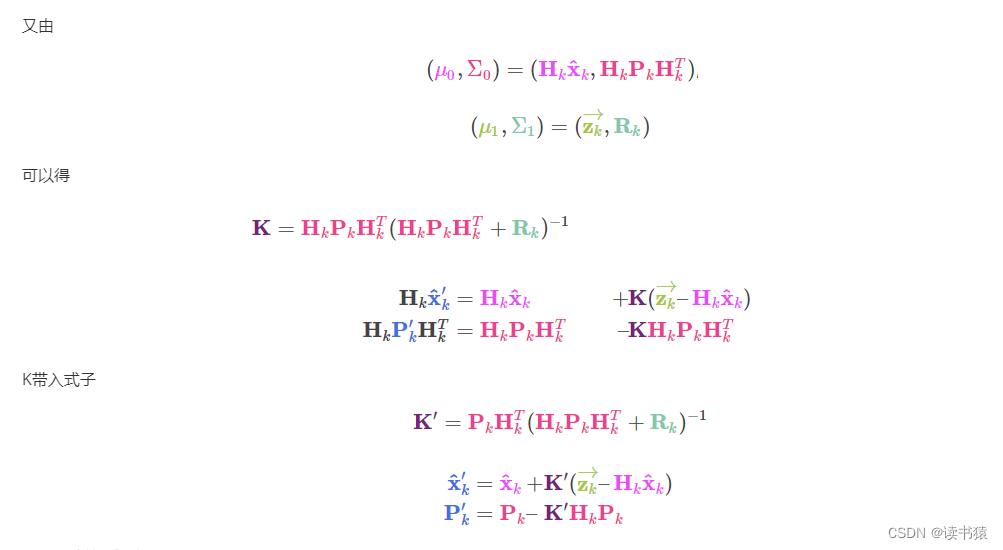前言
1、卡尔曼滤波(Kalman filtering)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波)过程。
2、在跟踪中卡尔曼滤波可以基于目标前一时刻的位置,来预测当前时刻的位置,并且可以比传感器更准确的估计目标的位置。
3、卡尔曼滤波不需要前面的历史数据,只需要前一时刻的状态数据就可以进行预测。
参考链接:https://www.kalmanfilter.net/background.html (kalman滤波保姆级教程)
一、卡尔曼滤波推导
1.1、设想场景
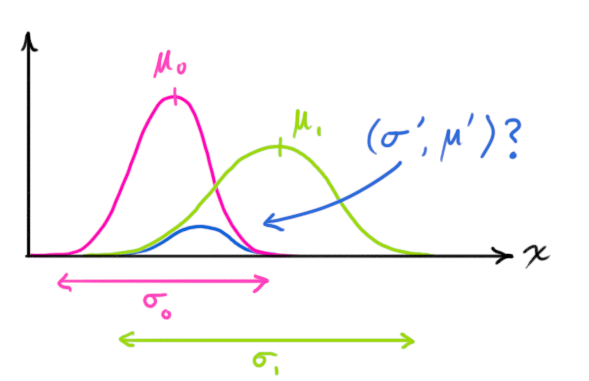
试想场景:小明正前方有一个人甲,小明用肉眼测量与甲距离为10m。假设小明和甲都静止不动,小明有个激光测距仪告诉小明与甲的距离分别为9.9m。
由于肉眼测量与激光测距仪的数据都不能确定为真值,那我们有没有办法结合他们的数据找个更准确的值呢?
假设小明肉眼估计的距离误差为 0.5m,激光测距仪误差0.2m
先来看看卡尔曼滤波如何做的 (后面会解释为什么这么做)
k = 0.5 * 0.5 / (0.5 * 0.5 + 0.2 * 0.2)
x = 10 + k * (9.9 - 10)
k = (1 - k) * (0.5 * 0.5)
...
1.2、一维公式推导
卡尔曼滤波基于高斯分布来建立状态方程。
在已有的测量数据情况下,我们要尽可能找到一个更加准确的值。
我们要获取更加准确值,我们需要同时符合两者假设条件。假定两者都属于正态分布,我们把两个高斯分布相乘,结果正好可以获得另一个放缩的高斯分布,得到了这个我们认为是最大后验概率分布。
可以手动推导下:
现在获得一个新的高斯分布。此时
令相同部分为K
则
一定要手动推导一下,然后回过头看我们假设的场景。
1.3、类比多维
我们通过第一个场景得到
这个是通过一维高斯分布获得的,现在我们类比下多维高斯分布
二、代码示例
2.1、一维空间
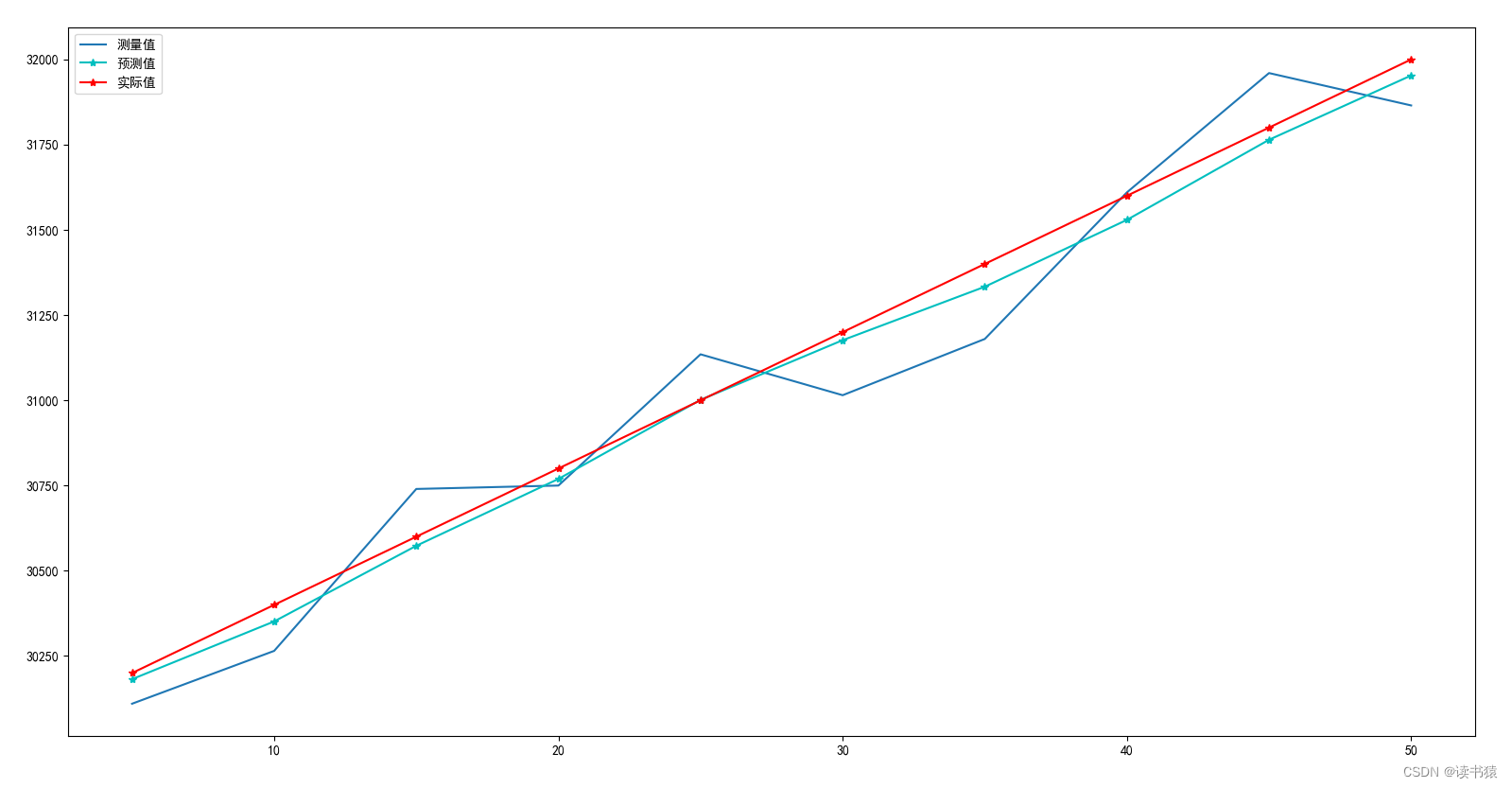
例1:假设飞行器沿某一个方向做匀速运动
v = 40m/s
测量值(m) 30110 30265 30740 30750 31135 31015 31180 31610 31960 31865
测量间隔 5s
import matplotlib.pylab as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文
# https://www.kalmanfilter.net/multiExamples.html
# 测量值是 30110 30265 30740 30750 31135 31015 31180 31610 31960 31865
# 初始值设置为30000m 速度40m/s
t = 5 # 每5s更新一次
alpha, beta = 0.2, 0.1 # 手动设定卡尔曼增益
mes_list = [30110, 30265, 30740, 30750, 31135, 31015, 31180, 31610, 31960, 31865]
true_list = [30200 + i * 40 * t for i in range(len(mes_list))]
predict_list = []
x = [5 * (i + 1) for i in range(len(mes_list))]
init_s, init_v = 30000, 40
s = init_s + init_v * t
v = 40
for index, data in enumerate(mes_list):
delta = data - s
s0 = s # 存下s的值
s = s + alpha * delta
predict_list.append(s)
print("****距离", s)
v = v + beta * delta / t
print("速度", v)
s = s + t * v
plt.figure()
plt.plot(x, mes_list)
plt.plot(x, predict_list, "c*-")
plt.plot(x, true_list, "r*-")
plt.legend(["测量值", "预测值", "实际值"])
plt.show()
2.2、二维空间
1、我们会预测车体状态
2、我们会测量车体状态
测量值去修正预测值,得到新的状态继续预测,如此反复进行
import numpy as np
import matplotlib.pylab as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
"""
https://www.kalmanfilter.net/multiExamples.html
************** predict
X(n+1,n) = F*X(n,n)+G*U(n) + W(n) F状态转移矩阵 G控制矩阵 W(n)噪声 X(n)状态矩阵
P(n+1,n) = F*P(n,n)*(F转置) + Q P 状态协方差矩阵 Q 过程噪声
************** updata
Z(n) = H*X(n) + V(n) H测量矩阵 X(n)状态矩阵 Z(n) (x(n,measured),y(n,measured))当前位置 V(n)随机噪声向量
K(n) = P(n,n-1) * (H的转置) * [(H*P(n,n-1)*[H的转置]+R(n))-1]
K卡尔曼增益 H测量矩阵 P 当前状态不确定协方差矩阵 H测量矩阵 R(n)测量噪声协方差
X(n,n) = X(n,n-1) + K(n) * (Z(n)-H*X(n,n-1))
P(n,n) = (1-K(n)*H) * P(n,n-1) * [(1-K(n)*H)的转置] + K(n)*R(n)*[K(n)的转置]
"""
def updata_kalman(Z, X_P):
"""
:param Z:测量值
:param X:状态矩阵
:param P:状态协方差矩阵
:return:更新后的X,P
"""
X, P = X_P
Z_1 = np.array([Z]).T
# print(Z_1)
K_1 = P @ np.transpose(H) @ np.linalg.inv(np.dot(np.dot(H, P), np.transpose(H)) + R_n)
X = X + K_1 @ (Z_1 - H @ X)
P = (np.identity(6) - K_1 @ H) @ P @ np.transpose(np.identity(6) - K_1 @ H) + K_1 @ R_n @ np.transpose(K_1)
return X, P
def predict_kalman(X_P):
X, P = X_P
X = F @ X
P = F @ P @ np.transpose(F) + Q
return X, P
if __name__ == '__main__':
d_T = 1 # 时间间隔1s
sigma_a = 0.2 # 加速度误差0.2m/s2
sigma_x, sigma_y = 3, 3 # x、y测量距离误差3m
F = np.array([[1, 1, 0.5, 0, 0, 0],
[0, 1, 1, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 1, 0.5],
[0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 1]])
# print("状态转移矩阵:\n", F)
Q = np.array([[0.25, 0.5, 0.5, 0, 0, 0],
[0.5, 1, 1, 0, 0, 0],
[0.5, 1, 1, 0, 0, 0],
[0, 0, 0, 0.25, 0.5, 0.5],
[0, 0, 0, 0.5, 1, 1],
[0, 0, 0, 0.5, 1, 1]]) * sigma_a * sigma_a
# print("过程噪声矩阵:\n", Q)
R_n = np.array([[sigma_x ** 2, 0], [0, sigma_y ** 2]])
# print("测量噪声协方差:\n", R_n)
# 设定初始状态 位移、速度、加速度都为0
X_0_0 = np.array([[0, 0, 0, 0, 0, 0]]).T
# 设定初始状态协方差矩阵,初始值较高、开始卡尔曼增益较大
P_0_0 = np.array([[500, 0, 0, 0, 0, 0],
[0, 500, 0, 0, 0, 0],
[0, 0, 500, 0, 0, 0],
[0, 0, 0, 500, 0, 0],
[0, 0, 0, 0, 500, 0],
[0, 0, 0, 0, 0, 500]])
X_1_0 = np.dot(P_0_0, X_0_0)
P_1_0 = np.dot(np.dot(F, P_0_0), np.transpose(F)) + Q
H = np.array([[1, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0]])
############################## 第一次测量的值
Z_1 = np.array([[-393.66, 300.4]]).T
"""
############################## UPDATE
K_1 = np.dot(np.dot(P_1_0, np.transpose(H)), np.linalg.inv(np.dot(np.dot(H, P_1_0), np.transpose(H)) + R_n))
X_1_1 = X_1_0 + K_1 @ (Z_1 - H @ X_1_0)
P_1_1 = (np.identity(6) - K_1 @ H) @ P_1_0 @ np.transpose(np.identity(6) - K_1 @ H) + K_1 @ R_n @ np.transpose(K_1)
############################## PREDICT
X_2_1 = F @ X_1_1
P_2_1 = F @ P_1_1 @ np.transpose(F) + Q
"""
result = updata_kalman(Z_1, [X_1_0, P_1_0])
plt_x = [result[0][0][0]]
plt_y = [result[0][0][3]]
# print(result)
result = predict_kalman(result)
# print("第一次 result", result)
# 后续测量值集合
Z_list = []
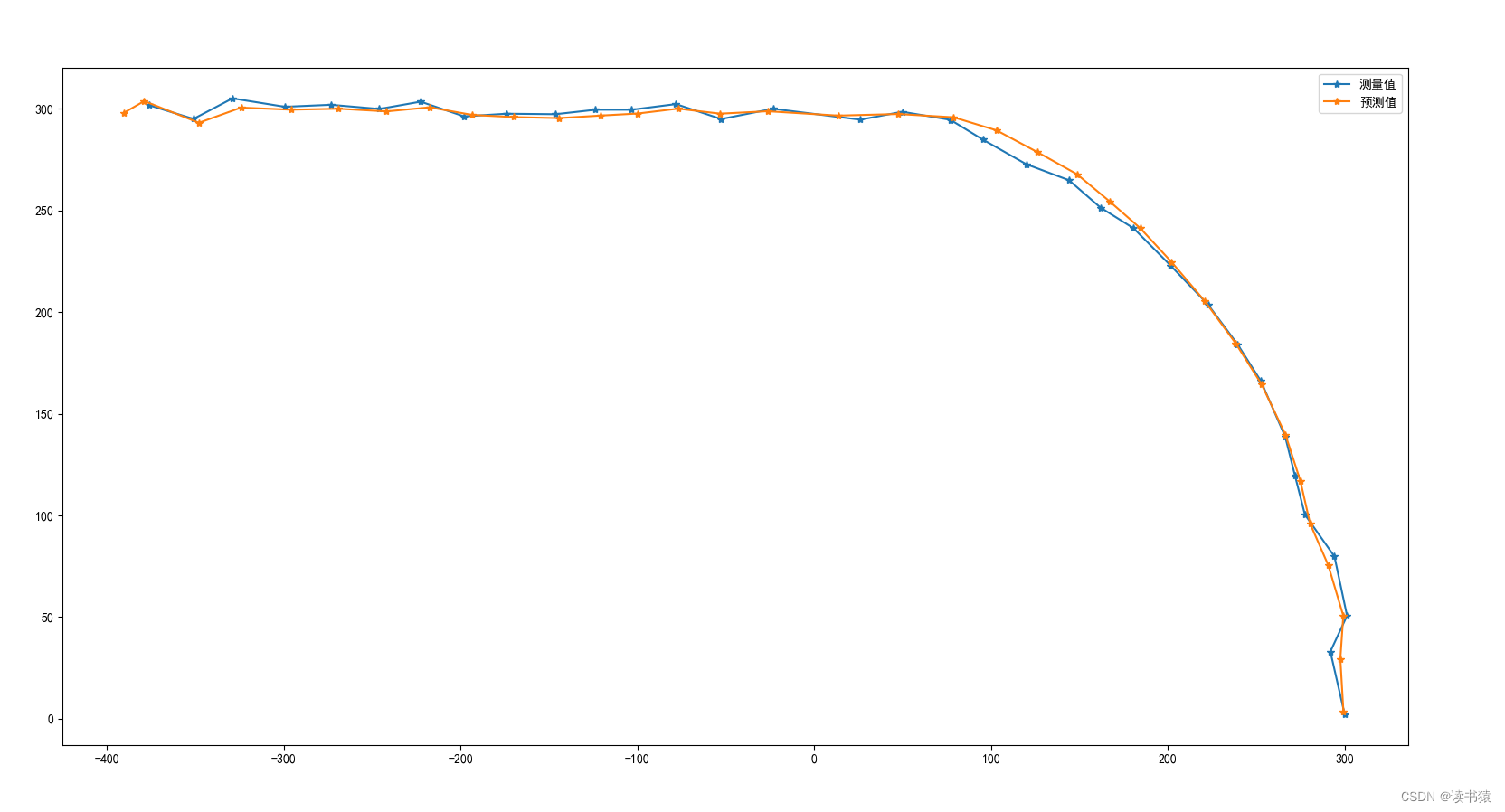
X_Z = "-375.93 -351.04 -328.96 -299.35 -273.36 -245.89 -222.58 -198.03 -174.17 -146.32 -123.72 -103.47 -78.23 -52.63 " \
"-23.34 25.96 49.72 76.94 95.38 119.83 144.01 161.84 180.56 201.42 222.62 239.4 252.51 266.26 " \
"271.75 277.4 294.12 301.23 291.8 299.89"
Y_Z = "301.78 295.1 305.19 301.06 302.05 300 303.57 296.33 297.65 297.41 299.61 299.6 302.39 295.04 300.09 " \
"294.72 298.61 294.64 284.88 272.82 264.93 251.46 241.27 222.98 203.73 184.1 166.12 138.71 119.71 100.41 " \
"79.76 50.62 32.99 2.14"
X_Z = list(map(float, X_Z.split("\t")))
Y_Z = list(map(float, Y_Z.split("\t")))
for i in range(len(X_Z)):
Z_list.append([X_Z[i], Y_Z[i]])
# 更新后的X,P 状态矩阵、状态协方差矩阵
result = updata_kalman([X_Z[i], Y_Z[i]], result)
plt_x.append(result[0][0][0])
plt_y.append(result[0][0][3])
# print(result)
# 预测下次的X,P
result = predict_kalman(result)
# print(result)
plt.figure()
plt.plot(X_Z, Y_Z, "*-")
plt.plot(plt_x, plt_y, "*-")
plt.legend(["测量值", "预测值"])
plt.savefig("result.jpg")
plt.show()