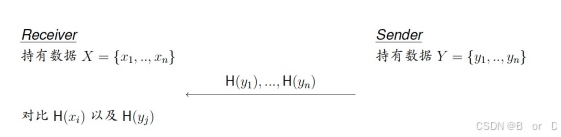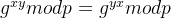第一讲理论基础：隐私求交PSI

安全求交集(PSI)定义

最常用基础的PSI

方法介绍

方法一：Method1 A Naïve PSI based on Hash

方法二：Method2 PSI Based on Diffie-Hellman Key Exchange

方法三：Method3 OPRF-based PSI

本文主要是记录参加隐语开源社区推出的第四期隐私计算实训营学习到的相关内容。

安全求交集(PSI)定义

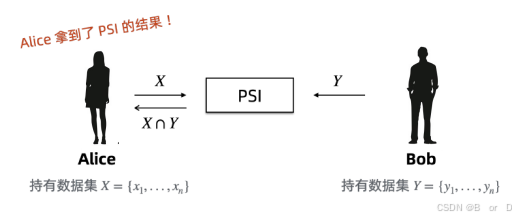
安全求交集（Private Set Intersection, PSI）是多方安全计算领域的一个子问题，通常也被称为安全求交、隐私保护集合交集或者隐私交集技术等，其目的是允许持有各自数据集的双方或者多方，执行两方或者多方集合的交集计算，当PSI执行完成，一方或者两方，甚至多方，能够得到交集结果，但是任意一方都无法获得交集以外的其他方集合数据的任何信息。下面是一个简单例子：

如上图所示，Alice 和 Bob 各有属于自己的数据集，分别为数据集X、Y，在经过 PSI 计算后，Alice 只能得到 X ∩ Y 部分，而不知道其他信息。也就是说 Alice 没有办法知道 Bob 的元素中不属于 X ∩ Y 的部分。如果 Alice 想尝试了解Bob的不匹配数据，Alice将无法成功。

最常用基础的PSI

本部分主要是以最常用基础的PSI: Two-Party Semi-Honest PSI为例对PSI进行介绍。

特点：

仅限于计算交集

交集可以被两方看见或其中一方看见，对非交集进行保护
两方PSI
半诚实安全

攻击者严格遵守协议，但是想要得到其他方的私密信息

挑战：

隐藏非交集元素（hiding）

当两个元素不相等时，必须附加某种“噪音”，使得不匹配的元素无法被穷举计算

计算交集元素（comparing）

当两个元素相等时，这种相等性应该能够被披露，而不受加“噪音”等的影响

效率高（efficiency）

方法介绍

方法一：Method1 A Naïve PSI based on Hash

（不安全）

基本思想：先hash后比较

加密hash：单向性、抗碰撞

各个挑战解决办法：

hiding：单向加密哈希函数功能
comparing：相同输入得到相同的hash输出
efficiency：hash是很快的

举个栗子：

如上图所示：Receiver 和 Sender 各有自己的数据X、Y，Sender 对数据Y内数据进行hash后发送给 Receiver，在Receiver 这边同样对自己的数据X进行hash并 Sender 发送过来的数据对比，整个过程Receiver 和 Sender都不知道对方的真实数据内容。

问题：

如果是高熵输入数据集，就像无限长度的随机字符串，那么这种方法没有问题。然而，在大多数现实世界的实现中，输入数据集的熵都很低，如 ID、电话号码等，那么就容易受到攻击，如暴力攻击。

方法二：Method2 PSI Based on Diffie-Hellman Key Exchange

基本思想：具有交换律的“双重加密”

各个挑战解决办法：

hiding：通过“加密”隐藏元素
comparing：交换律
efficiency：线性关系

这种方法是一种主流的PSI实现，因为随着密码原语的提升该方法也能得到提升。

协议设计：

离散对数问题（DLP）：假设 p、g、x、 y都是大正整数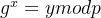， g^x = y mod p ，其中p是一个大素数，给出y、g、p，很难求出x。

hiding：给出y、g、p，很难求出x
comparing： $g^{xy}modp = g^{yx}modp$
efficiency：计算很快

举个栗子：

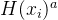
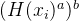
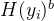
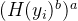
如上图所示：依据DH的基本思想，Receiver 有自己的数据X和密钥a，Sender 有自己的数据Y和密钥b。Receiver 首先对自己的数据X进行一次计算得到 H(x_i)^a 并发送给 Sender，Sender 接收到来自 Receiver 的数据后需要再次运算得到 (H(x_i)^a)^b 并发送给 Receiver，之后 Sender 还会对自己的数据Y进行一次计算得到 H(y_i)^b 并发送给Receiver，最后 Receiver 接收到来自 Sender 的数据后需要再次运算得到 (H(y_i)^b)^a 并对比和的值。

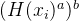
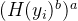
方法三：Method3 OPRF-based PSI

思想：

发送者需要根据自己的数据集计算“secret” function，之后发送给接收者；
接收者需要和发送者交互计算自己集合“secret” function后的值；
接收者将自己结果和来自发送者的结果进行比较；

各个挑战解决办法：

hiding：发送者不知道接收者的数据，接收者不知道“secret” function
comparing：比较经过“secret” function后的数据
efficiency：大部分都是像hash和对称密钥加密等的操作，只有小部分是PKI操作

协议设计：

OPRF: 发送者有一个密钥k，接收者输入一个元素e

计算F_k(e)
接收者知道F_k*(e)的输出，但是不知道k
发送者不知道输出以及输入元素e

OPRF for PSI：

接收者根据发送方的 k 值在自己的数据集上计算OPRF

接收者不知道发送者的k

发送者不知道接收者的数据集合
发送者根据自己的数据集合计算 ORPF，并将结果发送给接收者
接收方通过比较发送方的结果和自己的 OPRF 结果来找到交集

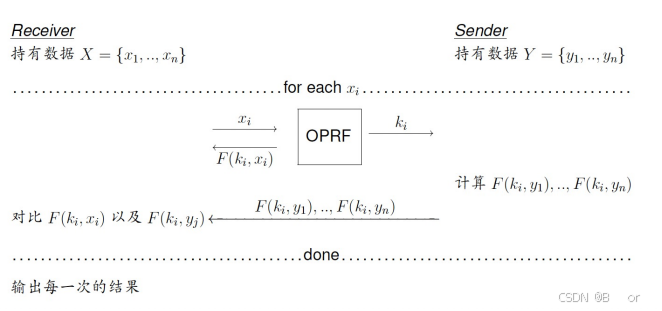
举个栗子：

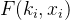
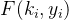
如上图所示：Receiver 有自己的数据X，Sender 有自己的数据Y。Receiver 需要和 Sender 交互对其数据X进行计算得到 F(k_i,x_i) ，之后 Sender 同样也需要计算出 F(k_i,y_i) 并发送给 Receiver ，Receiver 可以比较 Sender 的结果和自己的 OPRF 结果来找到交集。

其他思考

应用

白/黑明单, 撞库, 等等.

还有什么？

交集使用？
多方PSI?
计算模型?
安全模型?
非对称PSI?
其他特殊需求

交集使用

交集可能不是PSI交互双方的共有知识，在交集中的数据属于其他方。比如Alice在银行A和银行B各有一个账号，但是使用的是同一个唯一ID，那么在Alice允许的情况下，银行A和银行B可以通过PSI找到她。

挑战：交集“可用不可见”

case1：交集是机密的，但交集个数不是保密的

Method：

PHE + Polynomial evaluation [8]

DH-based PSI with shuffle [20]

case2：交集是机密的，但是需要在这个秘密的交集上附带运算。交集被“加密”，与“加密”交集相关的数据用于后续的安全计算，比如说在交集中带有有效载荷的PSI，其交集本身被隐藏在中间结果。

Method：

Circuit-based PSI [9]

DH-PSI with permutation and PHE [20]

Case 3: 交集是加密的，但是仍然需要被使用

Method：

FHE-PSI + Differential Privacy [10]

DH-PSI + Differential Privacy

多方PSI

常规多方PSI

动机：N方交互是需要的

挑战：任何两方之间的交集都不能被披露

Method

PHE+ Polynomial representation [8]

OPPRF [11]

特殊多方PSI

动机：可能需要计算两方之间的交集，并向特定方披露

挑战：

要求因情况而异

需要定制解决方案

Method：根据需求定制的 PSI 协议

计算模型

单向模型

动机：仅一方应了解交集。例如，客户端向新的社交媒体服务提交联系人列表，客户端了解集合的交集，服务器除了客户端输入的大小外，什么也不了解。

Method：OPRF-based PSI, etc.

互惠模型

动机：双方应该知道这个交集。比如在两个银行找到共同用户。

Method：DH-PSI, etc.

Outsourced/Delegated/Server-Aided PSI

动机：参与方不能完成PSI计算，比如资源受限设备

挑战：第三方仅仅帮助计算但是不能知道最终结果

在这种情况下第三方往往是大型的云服务提供商并且假设云提供者不会和用户合谋。通常的模型是云端协助PSI，得到加密的匹配结果，发送给客户端，然后客户端解密匹配结果。

Method：Polynomial representation + PHE + PRF [12]

安全模型

Semi-Honest Secure PSI

动机：简单、有效，并且大多数PSI协议是基于Semi-Honest实现的

挑战：安全假设太强，只考虑被动对手

Method: PSI based on DH, OPRF, etc. [1][2][3][5]

Malicious Secure PSI

动机：

提升安全
更加现实的安全假设，考虑恶意对手
恶意对手定义

挑战：更多的计算和通信开销

Method：PSI protocols with extra verification [7][13]

非对称PSI

动机：一方比其他方拥有更大量的元素。比如C/S场景，现实世界很多场景都需要非对称的PSI

挑战：常规 PSI 对于非对称 PSI 没有效

Method：

ECC-OPRF-PSI [21]

FHE PSI 14

其他特殊需求

Size-hiding [16]
Business scenario with customized requirements

参考：

隐语 · 实训平台

【隐私计算篇】隐私集合求交（PSI）原理深入浅出-CSDN博客

[1] Benny Pinkas, Thomas Schneider, Michael Zohner. Faster Private Set Intersection based on OT Extension, USENIX Security 2014

[2] Benny Pinkas, Thomas Schneider, Michael Zohner. Scalable Private Set Intersection Based on OT Extension, ACM Transactions on Privacy and Security, 2018

[3] Rakesh Agrawal, Alexandre V. Evfimievski, and Ramakrishnan Srikant. Information sharing across private databases. Proceedings of the 2003 ACM SIGMOD International Conference on Management of Data, 2003

[4] Emiliano De Cristofaro and Gene Tsudik. Practical private set intersection protocols with linear computational and bandwidth complexity, IACR Cryptology ePrint Archive, 2009:491, 2009

[5] Vladimir Kolesnikov, Ranjit Kumaresan, Mike Rosulek, and Ni Trieu. Efficient batched oblivious PRF with applications to private set intersection. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security,2016

[6] Peter Rindal and Phillipp Schoppmann. VOLE-PSI: fast OPRF and circuit-psi from vector-ole, Advances in Cryptology - EUROCRYPT 2021, 2021

[7] Peter Rindal and Srinivasan Raghuraman. Blazing fast PSI from improved OKVS and subfield VOLE. IACR Cryptology ePrint Archive, 2022:320, 2022

[8] Lea Kissner and Dawn Song, Privacy-Preserving Set Operations, Crypto 2005.

[9] Benny Pinkas, Thomas Schneider, Oleksandr Tkachenko, and Avishay Yanai. Efficient circuit-based PSI with linear communication. Advances in Cryptology - EUROCRYPT 2019

[10] Bailey Kacsmar , Basit Khurram , Nils Lukas , Alexander Norton , Masoumeh Shafieinejad , Zhiwei Shang, Yaser Baseri , Maryam Sepehri, Simon Oya, Florian Kerschbaum, Differentially Private Two-Party Set Operations, 2020 IEEE European Symposium on Security and Privacy.

[11 ]Vladimir Kolesnikov, Naor Matania, Benny Pinkas, Mike Rosulek, and Ni Trieu. Practical multi-party private set intersection from symmetric-key techniques. Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, 2017

[12] Abadi, Aydin, Sotirios Terzis, Roberto Metere, and Changyu Dong. Efficient Delegated Private Set Intersection on Outsourced Private Datasets, IEEE Transactions on Dependable and Secure Computing, 2017.

[13] Benny Pinkas, Mike Rosulek, Ni Trieu, and Avishay Yanai. PSI from paxos: Fast, malicious private set intersection. Advances in Cryptology - EUROCRYPT 2020

[14] Hao Chen, Kim Laine, Peter Rindal, Fast Private Set Intersection from Homomorphic Encryption, ACM CCS 2017

[15] Hao Chen, Zhicong Huang, Kim Laine, Peter Rindal, Labeled PSI from Fully Homomorphic Encryption with Malicious Security, CCS 2018

[16] Giuseppe Ateniese, Emiliano De Cristofaro, Gene Tsudik. (If) Size Matters: Size-Hiding Private Set Intersection, PKC 2011

[17] Benny Pinkas, Mike Rosulek, Ni Trieu, and Avishay Yanai. Spot-light: Lightweight private set intersection from sparse OT extension. Advances in Cryptology - CRYPTO 2019

[18] Adam Groce, Peter Rindal, and Mike Rosulek, Cheaper Private Set Intersection via Differentially Private Leakage, PoPETS 2019

[19] MesaTEE, GitHub - zjshen14/mesatee: A Framework for Universal Secure Computing

[20] Mihaela Ion, Ben Kreuter, Ahmet Erhan Nergiz, Sarvar Patel, Shobhit Saxena, Karn Seth, Mariana Raykova, David Shanahan, Moti Yung, On Deploying Secure Computing: Private Intersection-Sum-with-Cardinality, EuroS&P, 2020

[21] Amanda Cristina Davi Resende and Diego de Freitas Aranha, Faster Unbalanced Private Set Intersection, FC2018