支持向量机（SVM）

1. 什么是支持向量机？

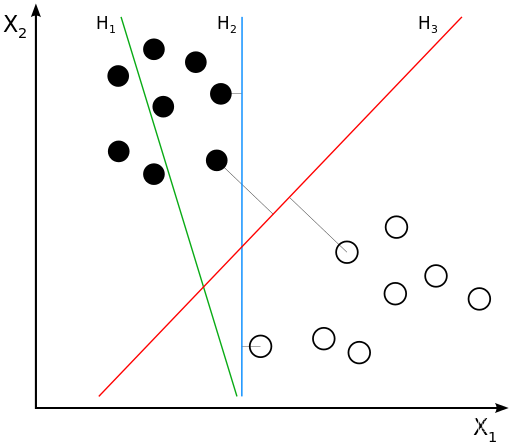
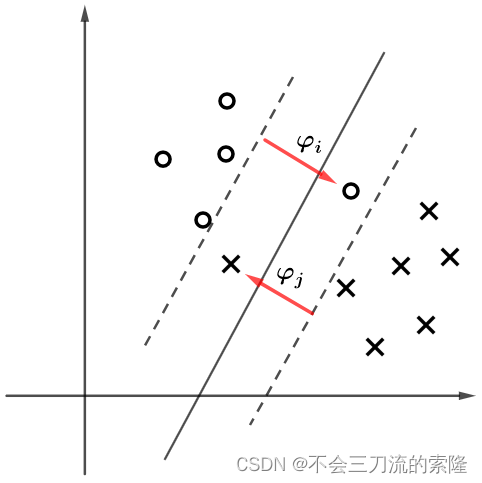
在上图中，我们想在二维平面中通过画出一条分界线将黑点与白点分开，很明显，我们认为在上面所画的三条分界线中$H_3$是最好的，因为$H_1$压根就没有达到分开的效果，$H_2$最近的数据点只有很小的间隔，如果测试数据有一些噪声的话可能就会被$H_2$错误分类(即对噪声敏感、泛化能力弱)。$H_3$以较大间隔将它们分开，这样就能容忍测试数据的一些噪声而正确分类，是一个泛化能力不错的分类器。

我们假设$H_3$就是最好的决策边界，不难发现，它距离两个类别的最近样本最远，所以我们也可以理解为是这两个类别的最近样本支撑着$H_3$的位置，我们将这样的样本称之为支持向量，之所以称为向量，是因为在实际分类中，一个样本是通过一个特征向量来描述的。

简言之，SVM就是一种二类分类模型，他的基本模型是的定义在特征空间上的间隔最大的线性分类器，SVM的学习策略就是间隔最大化。

支持向量机

• “支持向量”：两类数据中距离我们的决策边界（面）最近的点，这些点就被称为“支持向量”。

• “机”：是机器学习领域对一些算法的统称，常把算法看做一个机器，或者学习函数。

  那么我们回过头来重新理解一下维基百科对支持向量机的定义：

支持向量机（英语：support vector machine，常简称为SVM，又名支持向量网络）是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。

2. 证明推导

在分类工作中，有两种情况，一个是线性可分，一个是非线性可分，下面我们来逐一进行讲解

2.1 线性可分

线性可分的数学定义：

对于$D_0$、$D_1$两个点集，如果存在$n$维向量$W$和实数$b$，使得所有$D_0$中的点有 $W{x}_i+b>0$，$D_1$中的点有 $W{x}_i+b<0$，则称$D_0$与$D_1$两个点线性可分，其中 $Wx+b=0$ 即为分开$D_0$与$D_1$的超平面方程.

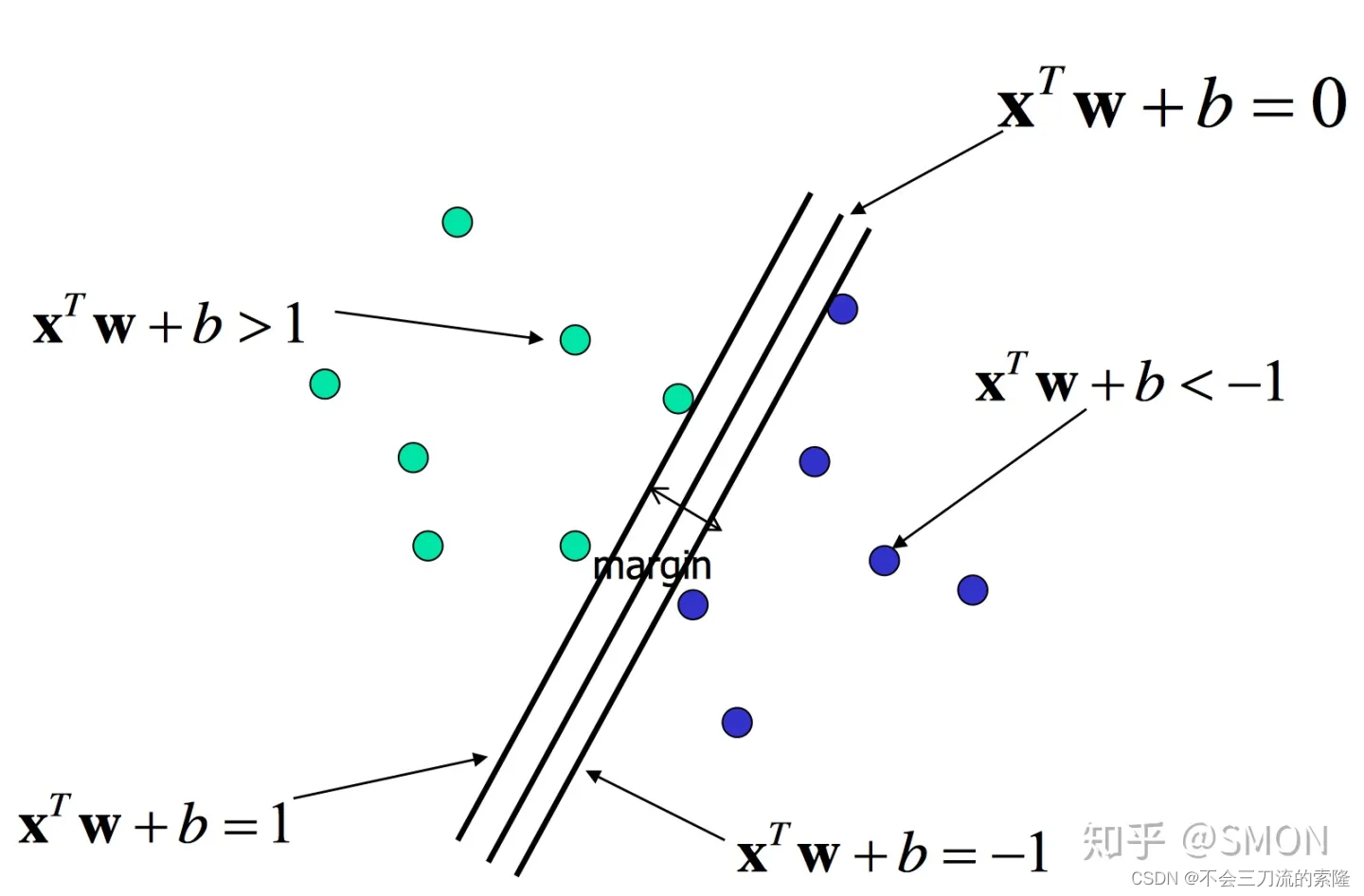
一个超平面由法向量$W$和截距$b$决定,其方程为$X^{T}W+b=0$, 可以规定法向量指向的一侧为正类,另一侧为负类（其样本带入超平面方程为-1）。下图画出了三个平行的超平面，法方向取左上方向。

为了找到最大间隔超平面，我们可以先选择分离两类数据的两个平行超平面，使得它们之间的距离尽可能大。在这两个超平面范围内的区域称为“间隔(margin)”，最大间隔超平面是位于它们正中间的超平面。这个过程如上图所示。

上文我们说到了正类与负类。正类的样本值带入超平面方程中满足 $W^{T}X+b\ge 1$，而负类就是 $W^{T}X+b\le -1$，因此为了统一计算，我们提出 $y_i(W^T{X}_i+b)\ge 1$，其中 $y_i=W^T{X}_i+b$，因此一个能够达到线性可分的超平面方程的一定满足 $y_i(W^T{X}_i+b)\ge 1$

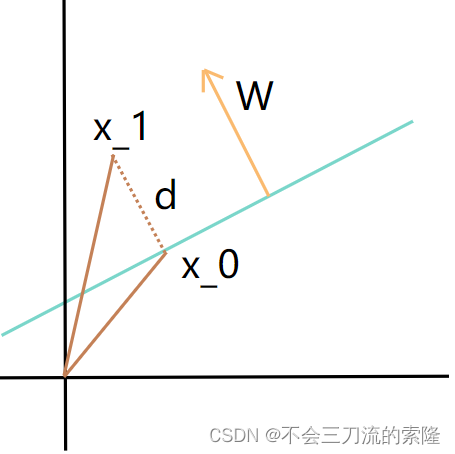
2.1.1 点到超平面距离推导

如上图，直线方程为 $W^{T}X+b=0$，$X_1$ 是直线外一点，$X_0$ 是直线上一点，即 $W^T{X}_0+b=0$，$d$ 是 $X_1$ 到直线的距离。

推导如下：
$$\begin{gathered} X_1=X_0+d\frac{W}{\Vert W\Vert } \\ {W}^{T}X=W^T{X}_0+d\frac{W\cdot W^T}{\Vert W\Vert }=-b+d\Vert W\Vert \\ d=\frac{W^{T}X+b}{\Vert W\Vert } \end{gathered}$$
如果 $X_1$ 在直线下方，则：
$$\begin{gathered} X_1=X_0-d\frac{W}{\Vert W\Vert } \\ d=-\frac{W^{T}X+b}{\Vert W\Vert } \end{gathered}$$
综上：
$$d=-\frac{\left|W^{T}X+b\right|}{\Vert W\Vert }$$
分式上下同时乘以 $\alpha$，得：
$$d=\frac{\alpha \left|W^{T}X+b\right|}{\alpha (\Vert W\Vert )}=\frac{1}{\Vert W^{{}^{\prime }}\Vert }$$
在下面推导SVM时，我们会用到 $d=\frac{1}{\Vert W^{{}^{\prime }}\Vert }$

2.2 线性可分的推导

间隔最大化：

margin的数学表达：(公式中的$X_0$是支持向量)
$$d=\frac{\left|W^T{X}_0+b\right|}{\Vert W\Vert }=\frac{\alpha \left|W^T{X}_0+b\right|}{\alpha \Vert W\Vert }=\frac{1}{\Vert W\Vert }$$
若令超平面方程的margin趋于最大，即$\Vert W\Vert$趋于最小，为了后续求导方便，我们在进行优化的时候会令$f(W)=\frac{1}{2}{\Vert W\Vert }^2$趋于最小，同时还应满足 $y_i(W^T{X}_i+b)\ge 1$

SVM的问题提出：

• 原函数：$f(W)=\frac{1}{2}{\Vert W\Vert }^2$
• 限制条件：$y_i(W^T{X}_i+b)\ge 1$

将问题进行数学表达：
$$\{\begin{array}{l}minf(W)\\ s.t.g(w,b)=1-y_i(W^T{X}_i+b)\le 0\end{array}({\alpha }_i\ge 0,i=1\sim n)$$
PS: $s.t.$ 是subject to的缩写，表示受限于。并且只有支持向量带入$g(W,b)$才会等于0，其余向量带入都小于0。

引入拉格朗日乘子法解决不等式约束优化问题

到现在，我们已经初步建立了问题模型（这是一个不等式优化问题），下一步就是对其进行优化求解，在这里我们是用拉格朗日乘子法解决不等式优化问题。
原问题变为：
$$L(W,b,\alpha )=\frac{1}{2}{\Vert W\Vert }^2+\sum _{i=1}^n{\alpha }_i[1-y_i(W^T{X}_i+b)]({\alpha }_i\ge 0,i=1\sim n)$$
在拉格朗日乘子法解决不等式约束优化问题时，往往会引入KKT条件，KKT条件是拉格朗日函数达到最优解使得必要条件，下面列出的就是$L(w,b,\alpha )$的KKT条件：
$$\{\begin{array}{l}\frac{\partial L}{\partial W}=W-{\sum }_{i=1}^n{\alpha }_i{y}_i{X}_i=0\\ \frac{\partial L}{\partial b}=-{\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ {\alpha }_i{g}_i(W,b)=0\\ {\alpha }_i\ge 0\\ g_i(W,b)\le 0\end{array}$$
有了KKT条件，我们的目标变成要找到一组$W^{\ast },b^{\ast },{\alpha }^{\ast }$使得其满足KKT条件。但实际中，往往无法直接通过KKT条件求出最优解，于是在这里SVM的证明要再次被转换思路。

采用对偶转变求解思路：
我们重新看一下$L(W,b,\alpha )$：
$$L(W,b,\alpha )=\frac{1}{2}{\Vert W\Vert }^2+\underset{1}{\underbrace{\sum _{i=1}^n{\alpha }_i[1-y_i(W^T{X}_i+b)]}}$$
在用大括号括起来的一部分中，$a_i\ge 0,g_i(W,b)\le 0$也就是说 $a_i\cdot g_i(W,b)\le 0$ 。而关于其具体取值，看下图，在最优解的地方（也就是在所有满足条件的情况中使得$f(W)$最小的地方），只有当$g_i(W,b)=0$时，也就是当前$X_i$是支持向量，条件才会起约束作用，此时，$\alpha \ge 0$；而当$g_i(W,b)、leq0$时，条件不起约束作用，${\alpha }_i=0$，因此最优解时，各参数满足 ${\alpha }_i{g}_i(W,b)=0$，也就是说最优解时，$a_i$与$g_i$的乘积的值为最大。

到这里，想必大家可以理解，即在满足${\alpha }_i\cdot g_i(W,b)$的值最大（值为$0$）的$W,b$中，找到一组解，使得$f(W)$最小，也就是先求解条件，再在满足条件的集合中找最优解，这种求解思路与直接暴力计算KKT完全不同，将其进行数学表达：
$${\min }_{W,b}{\min }_{\alpha }L(W,b)$$
但是，对上述式子的求解，要对其求导算极值，求导的时候发现又回到了KKT条件，这又回到了上面的窘境，于是对偶被引入了，将原问题对偶处理变成新的对偶问题：
$$\underset{W,b}{\min }\underset{\alpha }{\min }L(W,b)⟺\underset{\alpha }{\min }\underset{W,b}{\min }L(W,b)$$
之所以可以这样转换，是因为$L$函数是一个凸函数，所以满足强对偶定理。由于这里涉及凸优化理论，证明过程较为繁琐，这里就不过多赘述，感兴趣的同学可以查看凸优化理论这本书。

接下来，我们的目标变成对$\underset{\alpha }{\min }\underset{W,b}{\min }L(W,b)$的求解：
先看$\underset{W,b}{\min }L(W,b)$：
$${\min }_{W,b}L(W,b)\Rightarrow \{\begin{array}{l}\frac{\partial L}{\partial W}=W-{\sum }_{i=1}^n{\alpha }_i{y}_i{X}_i=0\\ \frac{\partial L}{\partial b}=-{\sum }_{i=1}^n{\alpha }_i{y}_i=0\end{array}\Rightarrow \{\begin{array}{l}W={\sum }_{i=1}^n{\alpha }_i{y}_i{X}_i\\ {\sum }_{i=1}^n{\alpha }_i{y}_i=0\end{array}$$
将这个结果带入L中可得，
$$L(W,b,\alpha )=\frac{1}{2}\sum _{i=1}^n{\alpha }_i{y}_i{X}_i^T\cdot \sum _j^n{\alpha }_j{y}_j{X}_j+\sum _{i=1}^n{\alpha }_i-\sum _{i=1}^n{\alpha }_i{y}_i{X}_i^T\cdot \sum _{j=1}^n{\alpha }_j{y}_j{X}_j=-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{X}_i^T{X}_j+\sum _{i=1}^n{\alpha }_i$$
于是问题变成了：
$${\max }_{\alpha }L={\max }_{\alpha }[-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{X}_i^T{X}_j+\sum _{i=1}^n{\alpha }_i]({\alpha }_i\ge 0,i=1\sim n)$$

到这里总结一下我们的优化进度，问题只需要对一个变量$\alpha$进行求解，同时，$W,b$均可用$\alpha$来表示：
最优解情况，满足$\frac{\partial L}{\partial W}=0$，故
$$W=\sum _{i=1}^n{\alpha }_i{y}_i{X}_i$$
挑选一个支持向量带入$g(W,b)=1-y_i(W^T{X}_i+b)$中，此时
$$g(W,b)=0,b=\frac{1-y_i{W}^T{X}_i}{y_i}$$
也可以多找几个支持向量，求其平均值，以提高模型鲁棒性。

这里有一个小问题，怎样找到最优解情况下分解超平面的支持向量呢？
上面我们讲到，一个 ${\alpha }_i$ 对应一个 $X_i$ 的约束，而在SVM的约束中，只有支持向量的约束条件起作用，即 $g_i(W,b)=0$，并且只有此时，${\alpha }_i\ne 0$，故只需要遍历全部的 $\alpha$，对应不为$0$的下标 $i$ 对应的特征向量 $X_i$ 即为支持向量。

显然，证明问题还没有结束，还要解决 $\underset{\alpha }{\max }L$，但到了这里，还要再说明一下，上述证明只是分类问题中最理想化的情况——线性可分，所以在这里再去接着求解 $\underset{\alpha }{\max }L$会使得问题得不到普适化，因此，我们先暂时将 $\underset{\alpha }{\max }L$搁置一下，看一下线性不可分时，SVM问题变成了什么新的样子。

2.2 线性不可分

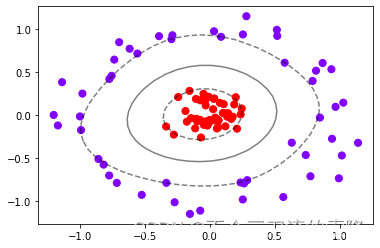
线性不可分与线性可分相对，即无法在$D_0$和$D_1$点集中找到一个线性分界线，对于线性不可分我们会采取两种方式，一个是软间隔，一个是升维（将样本点从较低纬度映射到更高维度）

2.2.1 软间隔

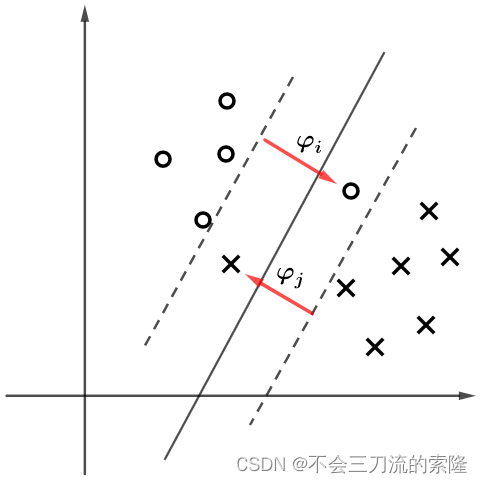
如下图，我们允许在间隔中存在个别的几个点，以提高模型的鲁棒性，这样间隔就不硬生生的将两个区域分开，因此我们形象的称之为软间隔。那对于间隔内的点，$y_i\cdot g_i(W,b)=y_i[W^T{X}_i+b]\le 1$，因此约束条件发生了变化：$1-y_i(W^T{X}_i+b)\ge 0$，为了让其符合最闲的约束条件，引入了一个松弛变量 ${\xi }_i$，令 ${\xi }_i\ge 0$，则 $1-y_i(W^T{X}_i+B)-{\xi }_i\le 0$，在这里只有在间隔内的样本 ${\xi }_i$ 才有意义，间隔外的其他样本 ${\xi }_i=0$.

这里应注意，${\xi }_i$应尽可能小，如果他非常大，则模型会允许间隔内存在许多样本，造成间隔过度软的情况，如下图。

于是为了令${\xi }_i$尽可能小，在优化过程中将其加入$\underset{W}{\min }\frac{1}{2}{\Vert W\Vert }^2$中，将其变成 $\underset{W,\xi }{\min }(\frac{1}{2}{\Vert W\Vert }^2+C{\sum }_{i=1}^m{\xi }_i)$，其中$C$是一个超参数，在训练过程中，通过改变$C$的大小来控制${\xi }_i$的大小，若令$C$非常大，则模型为了最小化，会会使得${\xi }_i$尽可能更小。

到了这里原问题变成了：
$$\{\begin{array}{l}\underset{W,\xi }{\min }f(W,\xi )=\frac{1}{2}{\Vert W\Vert }^2+C{\sum }_{i=1}^m{\xi }_i\\ s.t.g_i(W,b)=1-y_i(W^T{X}_i+B)-{\xi }_i\le 0,h_i({\xi }_i)=-{\xi }_i\le 0\end{array}(i=1\sim n)$$
对于优化软间隔，在实际中会更倾向使用 Hinge Loss这一损失函数，Hinge loss在文章末会展开介绍。

2.2.2 软间隔无法解决的线性不可分

上图的左边，我们就算是使用软间隔技巧，仍然无法明确将这两个类别分开，于是，我们使用到了升维，即将样本点从较低维度映射到更高维度，所以我们应找到一个低维到高维映射的函数$\varphi (x)$（输入为低维向量，输出为高维向量），但是找到这样一个映射函数是非常困难的，而且就算在当前数据集中找到，其他的数据集可能又不能使用，很难普适化，这又是一个很棘手的问题，但是在SVM中，我们不用明确知道$\varphi (x)$具体表达式，因为在后面，我们会使用核函数技巧，非常巧妙地将此难题化解，所以我们先暂时使用$\varphi (x)$。
到这，原问题变成了：
$$\{\begin{array}{l}\underset{W,\xi }{\min }f(W,\xi )=\frac{1}{2}{\Vert W\Vert }^2+C{\sum }_{i=1}^m{\xi }_i\\ s.t.g_i(W,b)=1-y_i(W^T{X}_i+B)-{\xi }_i\le 0,h_i({\xi }_i)=-{\xi }_i\le 0\end{array}(i=1\sim n)$$
同样应用拉格朗日乘子法，因为存在两个不等式约束条件，所以在这里有两个拉格朗日乘子：
$$L(W,b,\xi ,\alpha ,\beta )=-\frac{1}{2}{\Vert W\Vert }^2+C\sum _{i=1}^m{\xi }_i+\sum _{i=1}^n{\alpha }_i[1-y_i(W^T\varphi (X_i)+b)-{\xi }_i]-\sum _{i=1}^n{\beta }_i{\xi }_i({\alpha }_i\ge 0,{\beta }_i\ge 0,i=1\sim n)$$
在这里的求解步骤与上述线性可分一致：

• 同样，最优解的求解等价于 $\underset{W,b,\xi }{\min }\underset{\alpha ,\beta }{\max }L$，原理与上文一致。
• 同样，满足强对偶定理，$\underset{W,b,\xi }{\min }\underset{\alpha ,\beta }{\max }L⟺\underset{\alpha ,\beta }{\max }\underset{W,b,\xi }{\min }L$
  对$W,b,\xi$求极值：
  $$\{\begin{array}{l}\frac{\partial L}{\partial W}=W-{\sum }_{i=1}^n{\alpha }_i{y}_i{\varphi }_i(X_i)=0\\ \frac{\partial L}{\partial b}=-{\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ \frac{\partial L}{\partial \xi }=C-{\alpha }_i-{\beta }_i=0\end{array}$$
  将上述等式带入$L$中，得：
  $$\underset{W,b,\xi }{\min }L(W,b,\xi ,\alpha ,\beta )=-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\varphi }^T(X_i)\varphi (X_j)+\underset{C-{\alpha }_i-{\beta }_i=0}{\underbrace{C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^n{\alpha }_i{\xi }_i-\sum _{i=1}^n{\beta }_i{\xi }_i}}+\sum _{i=1}^n{\alpha }_i({\alpha }_i\ge 0,{\beta }_i\ge 0,i=1\sim n)$$
  故
  $$\underset{W,b,\xi }{\min }L(W,b,\xi ,\alpha ,\beta )=L(\alpha ,\beta )=L(\alpha )=-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\varphi }^T(X_i)\varphi (X_j)+\sum _{i=1}^n{\alpha }_i({\alpha }_i\ge 0,i=1\sim n)$$
  下一步，进行$maxL(\alpha )$，这里为了方便我们在表达${\varphi }^T(X_i)\varphi (X_j)$时，采用函数$K(X_i,X_j)={\varphi }^T(X_i)\varphi (X_j)$来表示，之这里的$K(X_i,X_j)$就是上文所说的核函数，关于核函数后文会详细解释，这里先说一下其性质$K(X_i,X_j)=K(X_j,X_i)$，这个很容易就能看出来，我们就不证明了。
  问题到这里就转变为：
  $$\{\begin{array}{l}maxL(\alpha )=-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\varphi }^T(X_i)\varphi (X_j)+{\sum }_{i=1}^n{\alpha }_i\\ s.t.0\le {\alpha }_i\le C,{\sum }_{i=1}^n{\alpha }_i{y}_i=0\end{array}$$
  看到这，我们发现最终需要优化的变量只有$\alpha$了，于是，SVM最后一个使用的优化算法smo引入了。

2.3 smo算法

smo算法与坐标上升算法类似，即每次只在一个维度上对变量进行优化。再看一遍条件中的 ${\sum }_{i=1}^n{\alpha }_i{y}_i=0$，不难发现，动了一个$alph{a}_i$等于零就不成立了，因此，每一次要优化${\alpha }_i,{\alpha }_j$两个变量，所以，smo的思想是每一次优化都优化一对（${\alpha }_i,{\alpha }_j$），将其他变量固定（即看作常数），随后进行求偏导等于零求得极值，进而不断迭代更新$\alpha$。

2.3.1 先计算未经修剪的 ${\alpha }_i^{new}$

根据smo的思想，原问题变为
$$\underset{{\alpha }_1,{\alpha }_2}{\max }G({\alpha }_1,{\alpha }_2)={\alpha }_1+{\alpha }_2-\frac{1}{2}{\alpha }_1^2{y}_1^{2}K(X_1,X_1)-\frac{1}{2}{\alpha }_2^2{y}_2^{2}K(X_1,X-2)-{\alpha }_1{\alpha }_2{y}_1{y}_{2}K(X_1,X_2)-{\alpha }_1{y}_1\sum _{i=3}^n{\alpha }_i{y}_{i}K(X_1,X_i)-{\alpha }_2{y}_2\sum _{i=3}^n{\alpha }_i{y}_{i}K(X_2,X_i)-\underset{常数：C}{\underbrace{\frac{1}{2}\sum _{i=3}^n\sum _{j=3}^n{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(X_i,X_j)+\sum _{i=3}^n{\alpha }_i}}$$
根据 $$\sum _{i=1}^n{\alpha }_i{y}_i=0$$ 的条件，得出 ${\alpha }_1{y}_1+{\alpha }_2{y}_2=-{\sum }_{i=3}^n{\alpha }_i{y}_i=m$，两边同时乘$y_1$，因$y_1^2=1$，得${\alpha }_1=m{y}_1-{\alpha }_2{y}_1{y}_2$，同时令$V_1={\sum }_{i=3}^n{\alpha }_i{y}_{i}K(X_1,X_i),V_2={\sum }_{i=3}^n{\alpha }_i{y}_{i}K(X_2,X_i)$，进而简化了$W$，得
$$G({\alpha }_2)=m{y}_1-{\alpha }_2{y}_1{y}_2+{\alpha }_2-\frac{1}{2}(m-{\alpha }_2{y}_2{)}^{2}K(X_1,X_2)-\frac{1}{2}{\alpha }_2^{2}K(X_2,X_2)-(m-{\alpha }_2{y}_2){\alpha }_2{y}_{2}K(X_1,X_2)-V_1(m-{\alpha }_2{y}_2)-V_2{\alpha }_2{y}_2-V_2{\alpha }_2{y}_2+C$$
到这，$W$ 只有一个变量 ${\alpha }_2$ 了，为了求 $W$ 的最大值，我们对 ${\alpha }_2$ 求导，为了简化，我们用 $K_{i,j}$ 代替 $K(X_i,X_j)$
$$\begin{gathered} \frac{\partial G}{\partial {\alpha }_2}=-y_1{y}_2+1-{\alpha }_2{K}_{1,1}+m{y}_2{k}_{1,1}-{\alpha }_2{k}_{2,2}-m{y}_2{k}_{1,2}+2{\alpha }_2{k}_{1,2}+V_1{y}_2-V_2{y}_2=0 \\ \downarrow \\ (K_{1,1}+K_{2,2}-2k_{1,2}){\alpha }_2=y_2(y_2-y_1+m{K}_{1,1}-m{K}_{1,2}+V_1-V_2) \end{gathered}$$
上文我们得到
$$W=\sum _{i=1}^n{\alpha }_i{y}_i{X}_i$$
故超平面分解方程为：
$$f(X)=\sum _{i=1}^n{\alpha }_i{y}_{i}K(X,X_i)+b$$
将 $f(X)$ 带入 $V_1,V_2$ 中，然后将 $V_1,V_2$ 带入 $\frac{\partial G}{\partial {\alpha }_2}$所推出的等式中，可以得到：
$$(K_{1,1}+K_{2,2}-2K_{1,2}){\alpha }_2=y_2[\underset{E_1}{\underbrace{f(X_1)-y_1}}-\underset{E_2}{\underbrace{(f(X_2)-y_2)}}]+(K_{1,1}+k_{2,2}-2k_{1,2}){\alpha }_2$$
之所以在式子中写道 $f(X_1)-y_1$，是因为 $f(X_1)$ 是模型的输出，$y_1$ 是样本的标签，二者作差就是模型与真实值之间的误差。
令 $K_{1,1}+K_{2,2}-2K_{1,2}=\eta$，得：
$$\begin{gathered} {\alpha }_2^{new}=\frac{y_2(E_1-E_2)}{\eta }+{\alpha }_2^{old} \\ {\alpha }_1^{new}=(m-{\alpha }_2^{new}{y}_2)y_1 \end{gathered}$$

2.3.2 对 ${\alpha }_2^{new},{\alpha }_1^{new}$ 值进行修剪

回顾上面对 $\underset{W,b,\xi }{\min }\underset{\alpha ,\beta }{\max }L$ 进行求导时，得到 ${\alpha }_1{y}_1+{\alpha }_2{y}_2=C$，故 $0\le {\alpha }_i\le C$。

除此之外，还要满足${\sum }_{i=1}^n{\alpha }_i{y}_i=0$，得 ${\alpha }_1{y}_1+{\alpha }_2{y}_2=m$， 若 $y_1\ne y_2$，即 $y_1\cdot y_2=-1$，则 ${\alpha }_1-{\alpha }_2=m$，若 $y_1=y_2$，即 $y_1\cdot y_2=1$，则 ${\alpha }_1+{\alpha }_2=m$。

因此在求得 ${\alpha }_i^{new}$ 的值后，要根据上述条件对值的大小进行修剪。可见，这些限制均是现行的，故可用图来更清晰地观察：

当 $y_1\ne y_2$时：

• 下界：$L=max(0,{\alpha }_1^{old}-{\alpha }_2^{old})$
• 上界：$H=min(C,C+{\alpha }_1^{old}-{\alpha }_2^{old})$

当 $y_1=y_2$时：

• 下界：$L=max(0,{\alpha }_1^{old}+{\alpha }_2^{old}-C)$
• 上界：$H=min(C,{\alpha }_1^{old}+{\alpha }_2^{old})$

故求出的 ${\alpha }_1^{new},{\alpha }_2^{new}$ 的值要过一遍上下界阈值修剪：

• ${\alpha }_i^{new}<L\to {\alpha }_i^{new}=L$
• ${\alpha }_i^{new}>H\to {\alpha }_i^{new}=H$

2.3.3 对 ${\alpha }_i$ 迭代

上述过程仅举例了 ${\alpha }_1,{\alpha }_2$，实际要全部迭代，即将所有的 ${\alpha }_i$ 取出两个进行训练。即两层for循环，外面一层选 ${\alpha }_i$，里面一层选 ${\alpha }_j$。

3. 核函数

在SVM中，我们为了将样本值从低纬度映射到高维度，提出了寻找 $\varphi (X)$ 这个映射函数，然而这个映射函数很难确定，但是在后续的推导中，我们发现在使用 $\varphi (X)$ 函数时，总是成对使用，即 ${\varphi }^T(X)\varphi (X)$，正因有了这个特点，我们提出了核函数技巧：
$$K(X_1,X_2)={\varphi }^T(X_1)\varphi (X_2)$$
我们使用核函数将$X_1,X_2$ 与 ${\varphi }^T(X)\varphi (X)$ 进行映射，这样就大大减小运算量了，因为核函数的选取是非常多的，并且这样计算使得模型具有很强的普适化。

我们在实际解决问题的时候，甚至都不用关心它到底是如何映射的，只需要正确选用核函数，实现分类的目的即可。下面是一些常见的核函数，虽然大家都常见但用得最多的依旧是高斯核函数。

(1) 线性核（Linear Kernel）
$$k(x,z)=x^{T}z+C$$
其中 $C$ 为常数。

(2) 多项式核（Polynolial Kernel）
$$k(x,z)={\left(x^{T}z\right)}^d+C$$
其中 $C$ 为常数。

(3) 高斯核（Gaussian Kernel）
$$k(x,z)=\exp \left(-\frac{\Vert x-z{\Vert }^2}{2{\sigma }^2}\right)$$
其中， $\sigma >0$ 为高斯核的带宽 (width)。

(4) 拉普拉斯核（Laplacian Kernel）
$$k\left(x_i,x_j\right)=\exp \left(-\frac{\Vert x_i-x_j\Vert }{\sigma }\right),\sigma >0$$
(5) Sigmoid 核
$$k(x,z)=\tanh \left(\beta x^{T}z+\theta \right)$$
其中, thanh 为双曲正切函数, $\beta >0,\theta <0$ 。

通过前面的讨论可知，我们希望样本点在特征空间内线性可分，因此特征空间的好坏对支持向量机的性能至关重要。需要注意的是，在不知道特征映射的形式时，我们并不知道什么样的核函数的合适的，而核函数也仅是隐式地定义了这个特征空间。于是，核函数的选择称为支持向量机最大的变数。

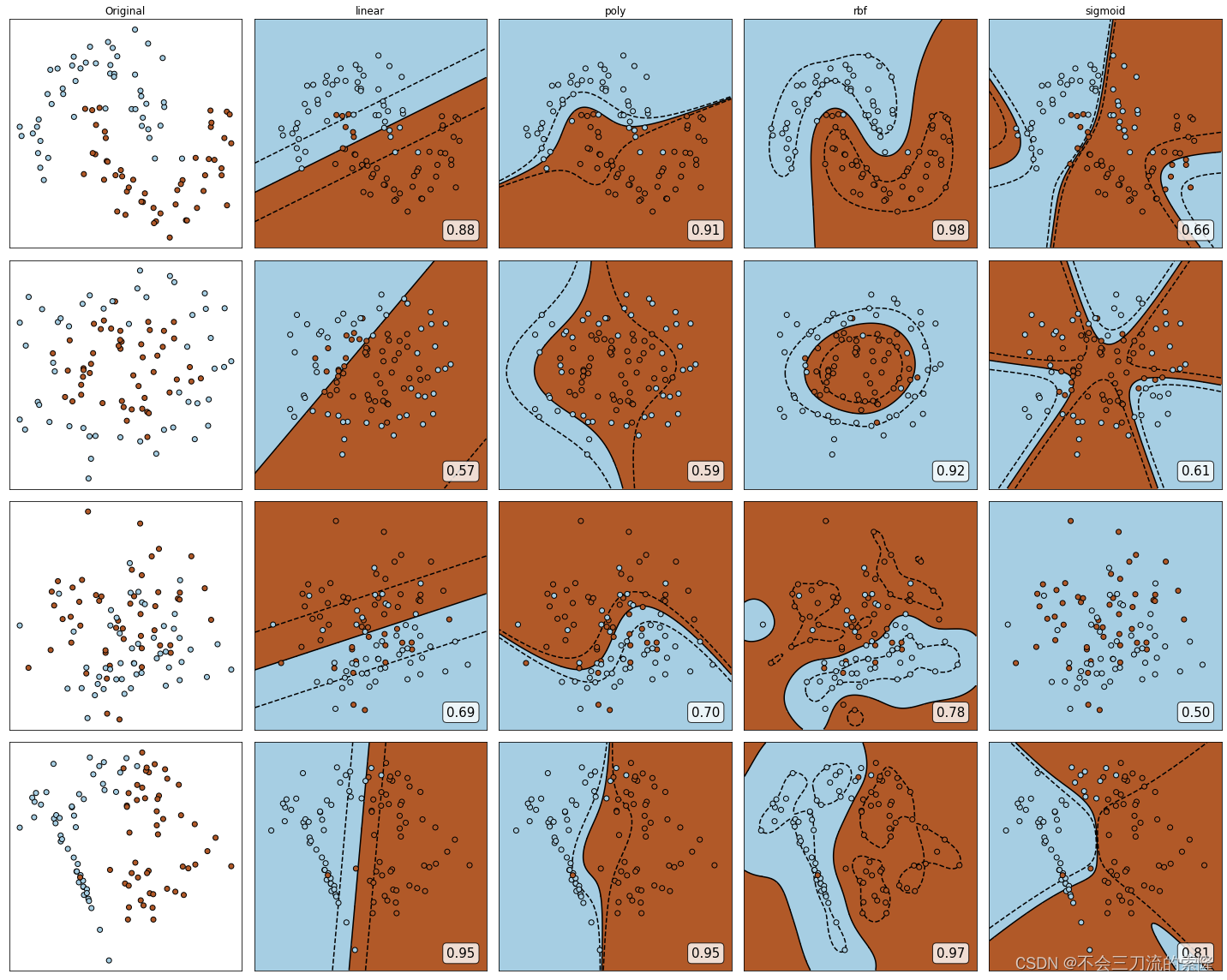
4. 代码实例（SVM决策边界可视化）

from sklearn.svm import SVC  # 导入SVM库
import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_circles
#制作数据集
X,y = make_circles(100, factor=0.1, noise=.1)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")

def plot_svc_decision_function(model,ax=None):
    if ax is None:
        ax = plt.gca()  # 获取画布
        
    xlim = ax.get_xlim()  # 取 X 轴的最小值与最大值
    ylim = ax.get_ylim()  # 取 Y 轴的最小值与最大值
    
    # 在最小值与最大值之间规律生成30个数
    x = np.linspace(xlim[0],xlim[1],30)  
    y = np.linspace(ylim[0],ylim[1],30)
    
    # 按照这三十个数生成网格种点的坐标
    Y,X = np.meshgrid(y,x)  
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    
    # 将所有的点的坐标给到决策函数，决策函数计算出的结果是点到决策平面的距离
    # 分别画出到决策平面距离为-1,0,1的等高线 其中 0 等高线就是决策超平面
    p_1 = model.decision_function(xy)
    P = model.decision_function(xy).reshape(X.shape)
    ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
    
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)
    
#f训练数据
clf = SVC(kernel = "rbf").fit(X,y)
plot_svc_decision_function(clf)

print('The writer of this article is ECJTU.')
plt.show()

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap #色彩块，好看一点
from sklearn.svm import SVC
from sklearn.datasets import make_circles,make_blobs,make_moons,make_classification#制作数据的类

#创建数据集，定义核函数的选择
n_samples=100

datasets=[
    make_moons(n_samples=n_samples,noise=0.2,random_state=0),
    make_circles(n_samples=n_samples,noise=0.2,factor=0.5,random_state=1),
    make_blobs(n_samples=n_samples,centers=2,random_state=5),
    make_classification(n_samples=n_samples,n_features=2,n_informative=2,n_redundant=0,random_state=5)
]
Kernel=["linear","poly","rbf","sigmoid"]  # 分别使用四个核函数进行训练
#构建子图
nrows=len(datasets)#子图的行数为数据集的数量
ncols=len(Kernel)+1
fig,axes=plt.subplots(nrows,ncols,figsize=(20,16))#figsize就是行列对应的尺寸

#第一层循环：在不同的数据集中循环
for ds_cnt, (X,Y) in enumerate(datasets):
    
    #在图像中的第一列，放置原数据的分布
    ax = axes[ds_cnt, 0]
    if ds_cnt == 0:
        ax.set_title("Original")
    ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired,edgecolors='k')
    ax.set_xticks(())
    ax.set_yticks(())
    
    #第二层循环：在不同的核函数中循环
    #从图像的第二列开始，一个个填充分类结果
    for est_idx, kernel in enumerate(Kernel):
        
        #定义子图位置
        ax = axes[ds_cnt, est_idx + 1]
        
        #建模
        clf = SVC(kernel=kernel, gamma=2).fit(X, Y)
        score = clf.score(X, Y)
        
        #绘制图像本身分布的散点图
        ax.scatter(X[:, 0], X[:, 1], c=Y
                   ,zorder=10
                   ,cmap=plt.cm.Paired,edgecolors='k')
        
  
        x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
        y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
        
        #np.mgrid，合并了之前使用的np.linspace和np.meshgrid的用法
        #一次性使用最大值和最小值来生成网格
        #表示为[起始值：结束值：步长]
        #如果步长是复数，则其整数部分就是起始值和结束值之间创建的点的数量，并且结束值被包含在内  
        XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
     
        Z = clf.decision_function(np.vstack([XX.ravel(), YY.ravel()]).T).reshape(XX.shape)
        
         #填充等高线不同区域的颜色,距离大于零的为一类小于零的为一类填充不同颜色      
        ax.pcolormesh(XX, YY, Z > 0, shading='auto', cmap=plt.cm.Paired)
        #绘制等高线
        ax.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
                    levels=[-1, 0, 1])
        
        #设定坐标轴为不显示
        ax.set_xticks(())
        ax.set_yticks(())
        
        #将标题放在第一行的顶上
        if ds_cnt == 0:
            ax.set_title(kernel)
            
        #为每张图添加分类的分数   
        ax.text(0.95, 0.06, ('%.2f' % score)
                , size=15
                , bbox=dict(boxstyle='round', alpha=0.8, facecolor='white')
                    #为分数添加一个白色的格子作为底色
                , transform=ax.transAxes #确定文字所对应的坐标轴，就是ax子图的坐标轴本身
                , horizontalalignment='right' #位于坐标轴的什么方向
               )
print('The writer of this article is ECJTU.')
plt.tight_layout()
plt.show()

最后的一些补充

还记得在软间隔的地方讲的 Hinge Loss 吗？

具体的推导可以看一篇知乎的文章，里面讲的非常详细。

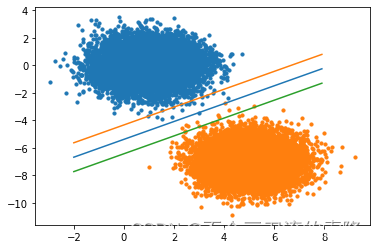
Hinge Loss 代码案例

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
torch.manual_seed(2)

class classify(nn.Module):
    def __init__(self,C=1):
        super(classify,self).__init__()
        self.w = nn.Parameter(torch.ones(2))
        self.b = nn.Parameter(torch.zeros(1))
        # C正相关越界点的个数 就是我们在上述推导过程中的超参数 C
        self.C = C
        self.relu0 = nn.ReLU()
        self.relu1 = nn.ReLU()
    def forward(self,x0,x1):
        w2 = torch.pow(self.w,2).sum()
        x0 = 1-(torch.matmul(x0,self.w) + self.b)
        x1 = 1+(torch.matmul(x1,self.w) + self.b)
        loss = self.relu0(x0).sum() + self.relu1(x1).sum()
        return loss/ self.C + w2 
    
model = classify(3)
opt = optim.SGD(model.parameters(),lr = 0.001)

torch.manual_seed(8)
x0 = torch.randn(10000,2) + torch.randn(10000,2) * 0.1 + torch.tensor([1,0])
x1 = torch.randn(10000,2) + torch.randn(10000,2) * 0.01  + torch.tensor([5,-7])
for i in range(200):
    loss = model(x0,x1)
    opt.zero_grad()
    loss.backward()
    if i %1000 ==0:
        print(model.w)
    opt.step()

plt.scatter(x0[:,0],x0[:,1],s =10)
plt.scatter(x1[:,0],x1[:,1],s =10)

x = torch.arange(-2,8,0.1)
yy = -(model.w[0] * x + model.b)/model.w[1]
yy1 = -(model.w[0] * x + model.b-1)/model.w[1]
yy2 = -(model.w[0] * x + model.b+1)/model.w[1]

print('The writer of this article is ECJTU.')
plt.plot(x,yy.data)
plt.plot(x,yy1.data)
plt.plot(x,yy2.data)

非常感谢你能够看完这篇文章，如果对你有帮助的话，点个赞再走呗🥳
​