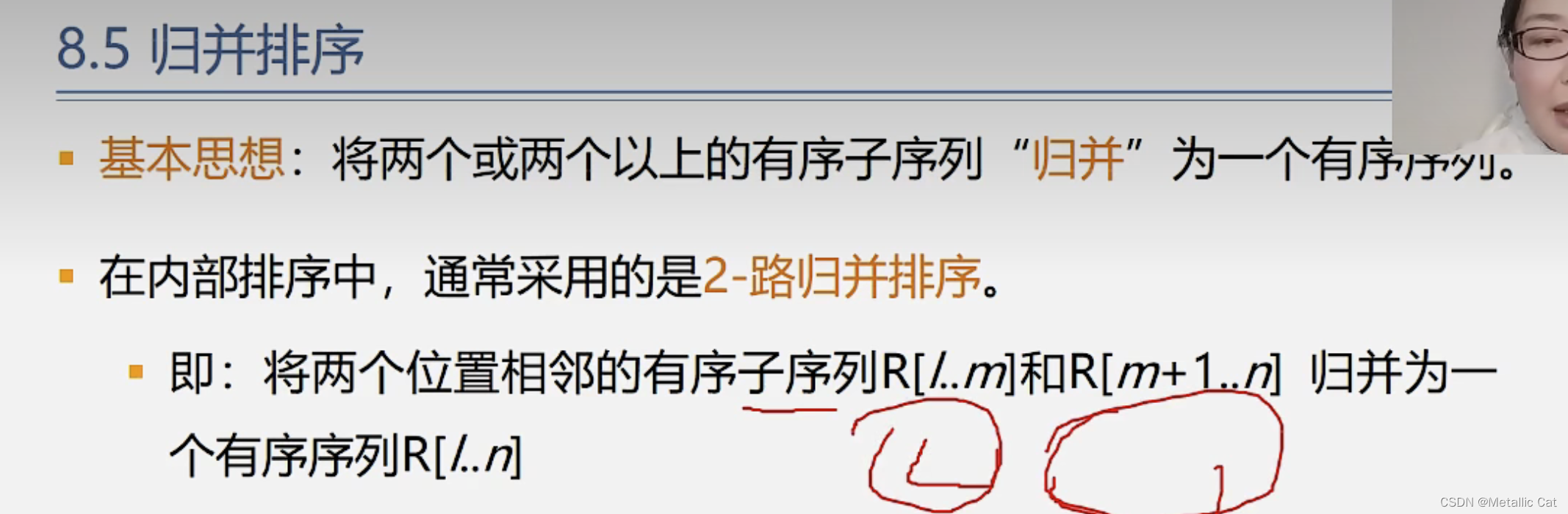
第一部分 --- 归并排序

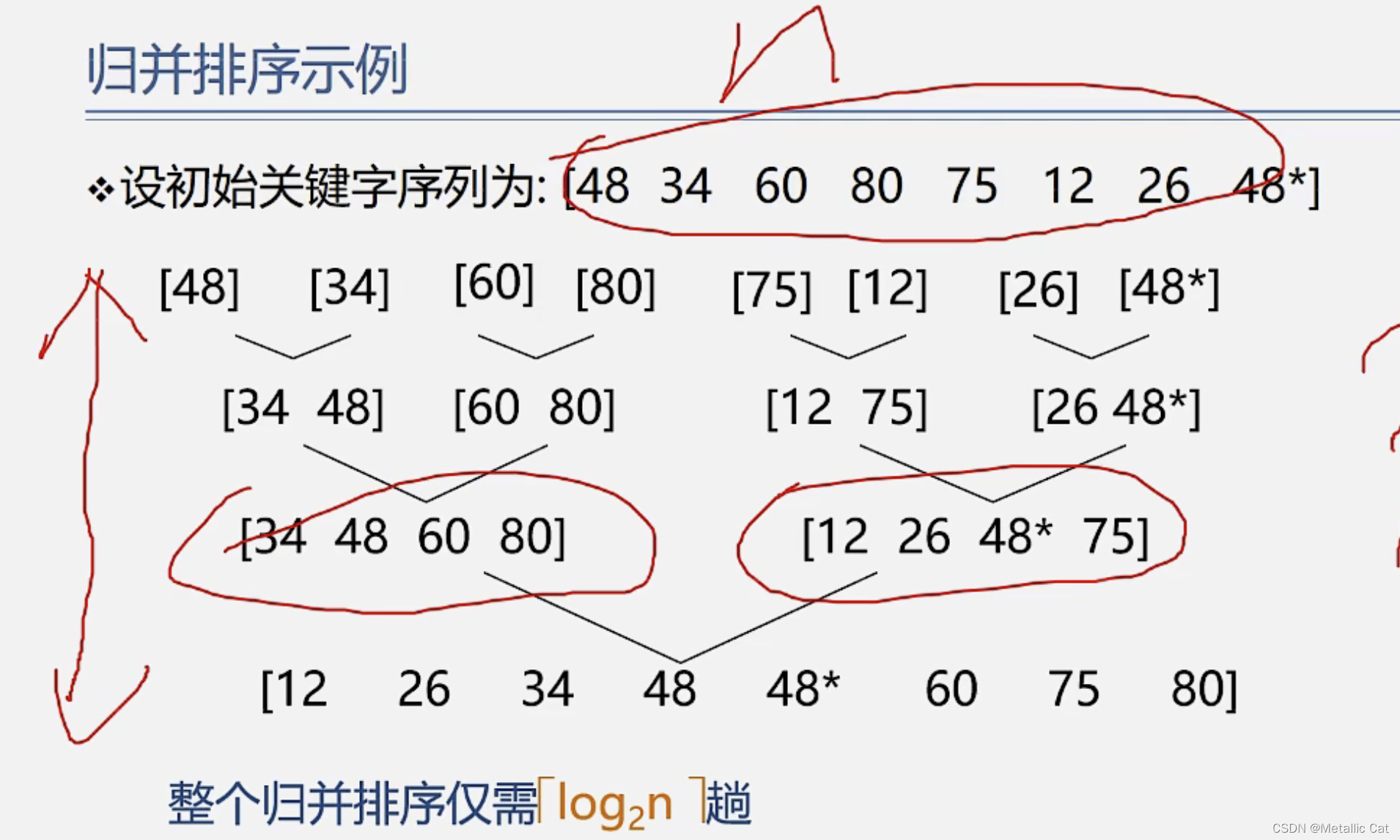
1.归并排序一次归并只能够归并两个相邻的有序子序列

2.归并排序的整个过程就是一棵倒着的树（如上），我们将这棵树称为归并树，树的层数就是我们进行归并操作的总趟数 --- 设完全二叉树的最后一层层数为K，则这一层的最大容量为 2的K-1次方，在归并排序中我们是已知完全二叉树的最后一层的最大元素总数的（就是我们要排序的元素总数），自然就能够得到树的最后一层层数，也就能得到总比较趟数了

3.如果说要对奇数个元素进行排序的话，我们需要先将两个相邻的元素进行归，使得等待归并排序的总子序列为偶数个，然后再开始正式对所有子序列进行归并排序

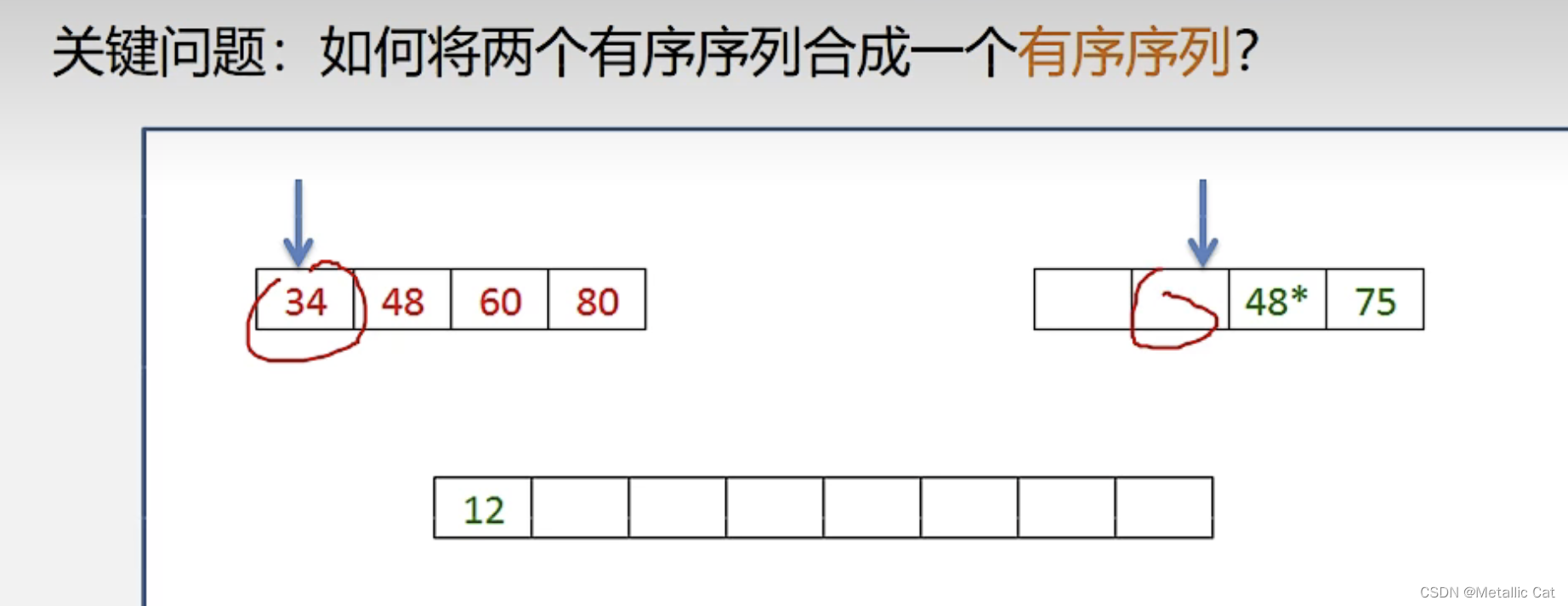
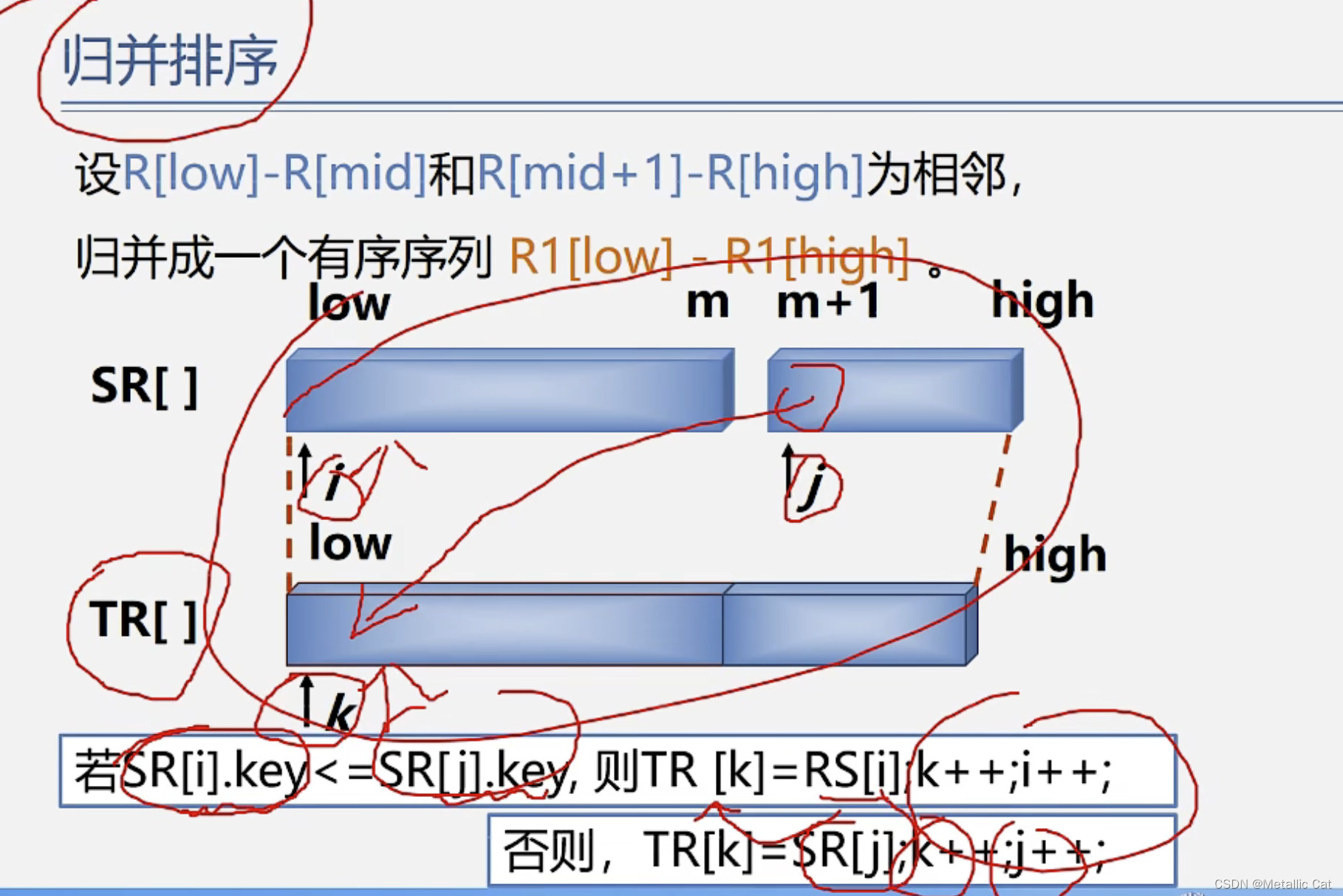
答案就是我们之前学过的双指针法：分别用两个指针指向两个有序序列的第一个元素（假设都是从小到大有序），比较两个元素谁更小，将较小的元素存到新的数组中，然后将指向这个较小元素的指针++，接着继续比较

直到两个序列或者是某个序列所有元素都比较完毕时停止比较，如果存在序列还有剩余元素没有比较的话，直接将这一段剩下的元素存到新的数组的最后一个元素后面

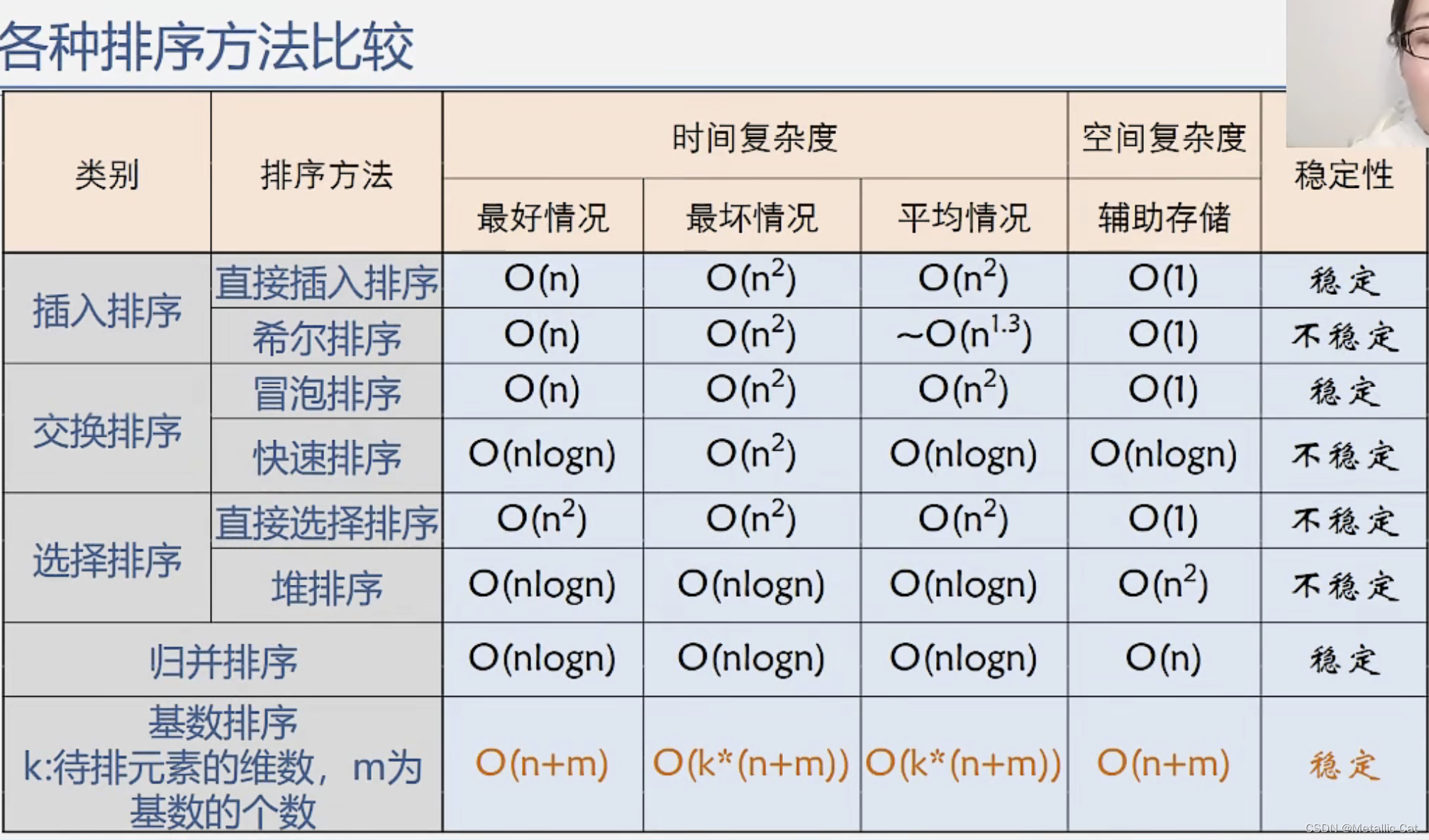
 1.设有n个元素，所有的元素都要比较一次 --- n --- 总共要比较 log2n趟 --- 总时间复杂度为O（n*log2n）

第二部分 --- 基数排序 

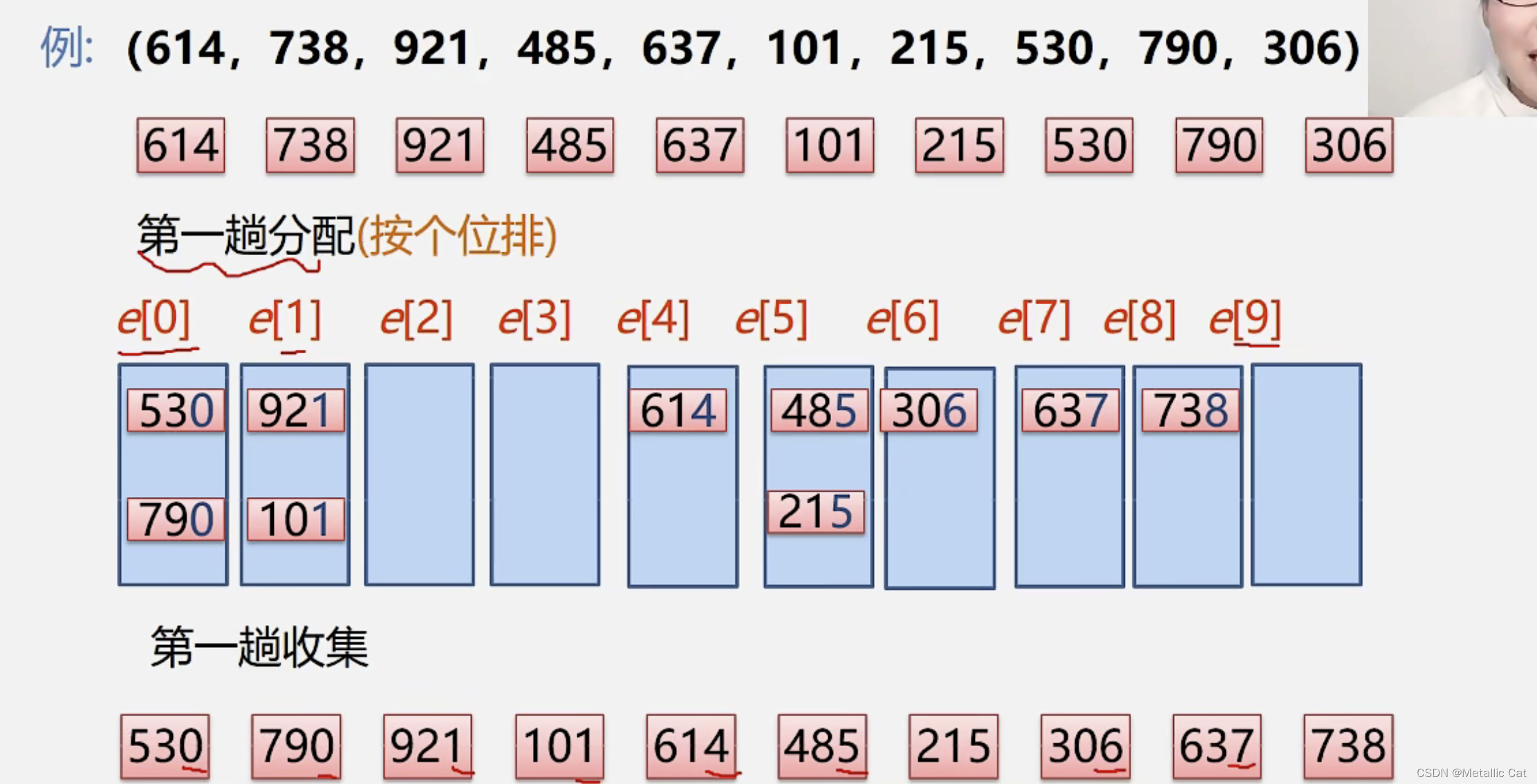
1.我们在进行分配的时候是从左往右检索分配的，第一次分配之后待排序元素在个位层次上是有序的，此时进行第二次分配，从左往右依次检索符合要求的元素并将其扔入桶中 --- 

此时扔到桶中的元素依然保持个位有序，同时它们的十位相等

2.分配的过程中就包含了排序，进行收集的时候我们得到的就是有序的序列了

1.任意多个数字进行排序后，我们得到的有序序列的构造一定可以进行这么几个分区：

首先是按照最大位数的大小进行分区排序，然后是在分号的区中按照次大位数的大小再次进行分区排序，接着是再次在分好的区中按照次次大位数的大小进行分区排序，就这样不停的分区排序，直到在最小位数分区排序完毕后停止排序

2.基数排序或者说桶排序的思想则是上面这个思想逆过来执行：

按照从左到右的顺序依次检索每一个元素，根据最小位数进行分区排序（分配到桶）

接着按照桶的顺序依次收集每个桶中的元素回到数组中 --- 此时最小位数分区有序

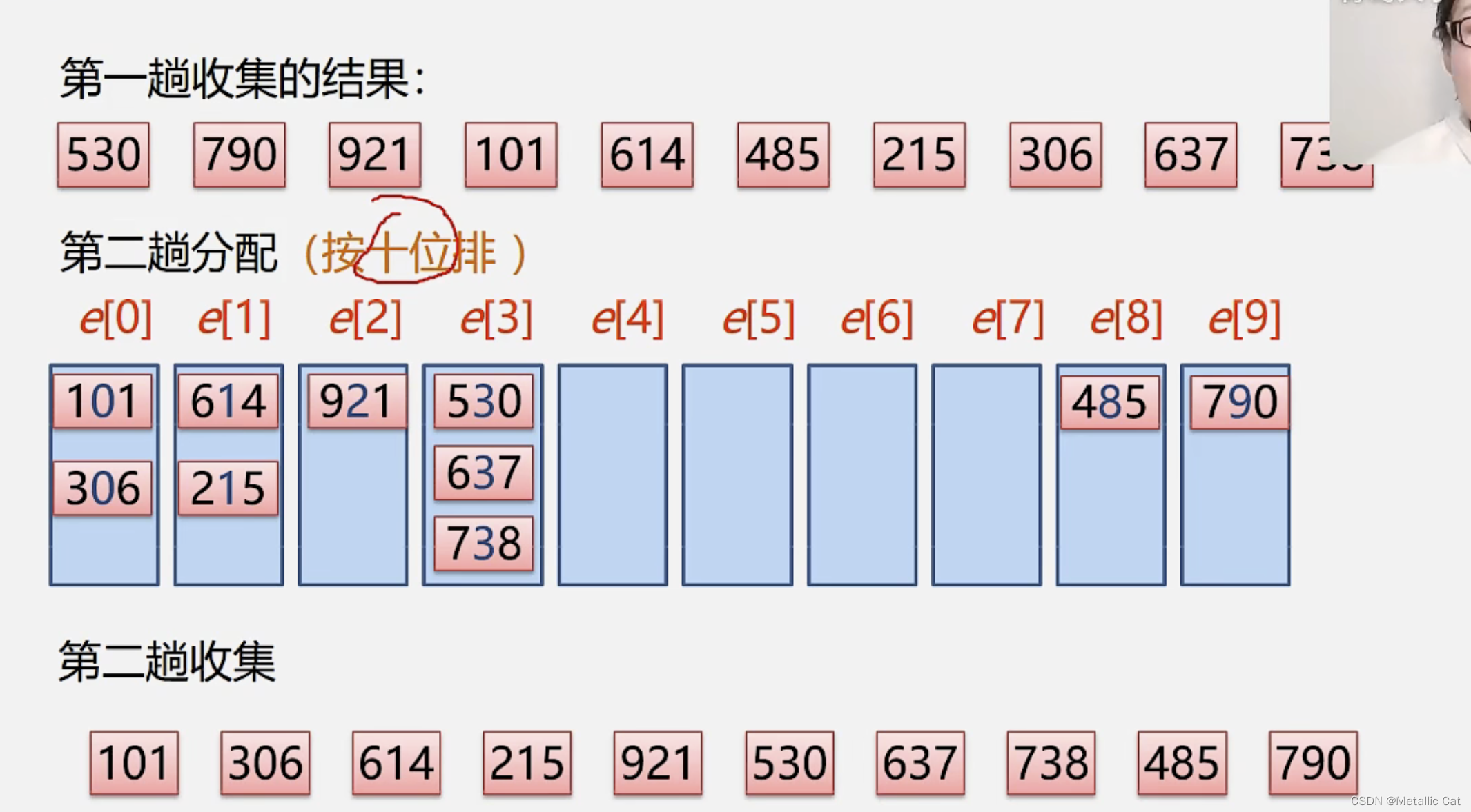
接着再次从左往右按照第二小位数的大小将元素检索分桶（这一步是建立在最小位元素分区有序的基础上的）

本质上就是先大层级排序，然后每个大层级中的小层级进行排序的逆过程 --- 即所有小层级排好序，然后每个大层级来选择自己的小层级，接着再将大层级排好序，这样的话就整体排好序了

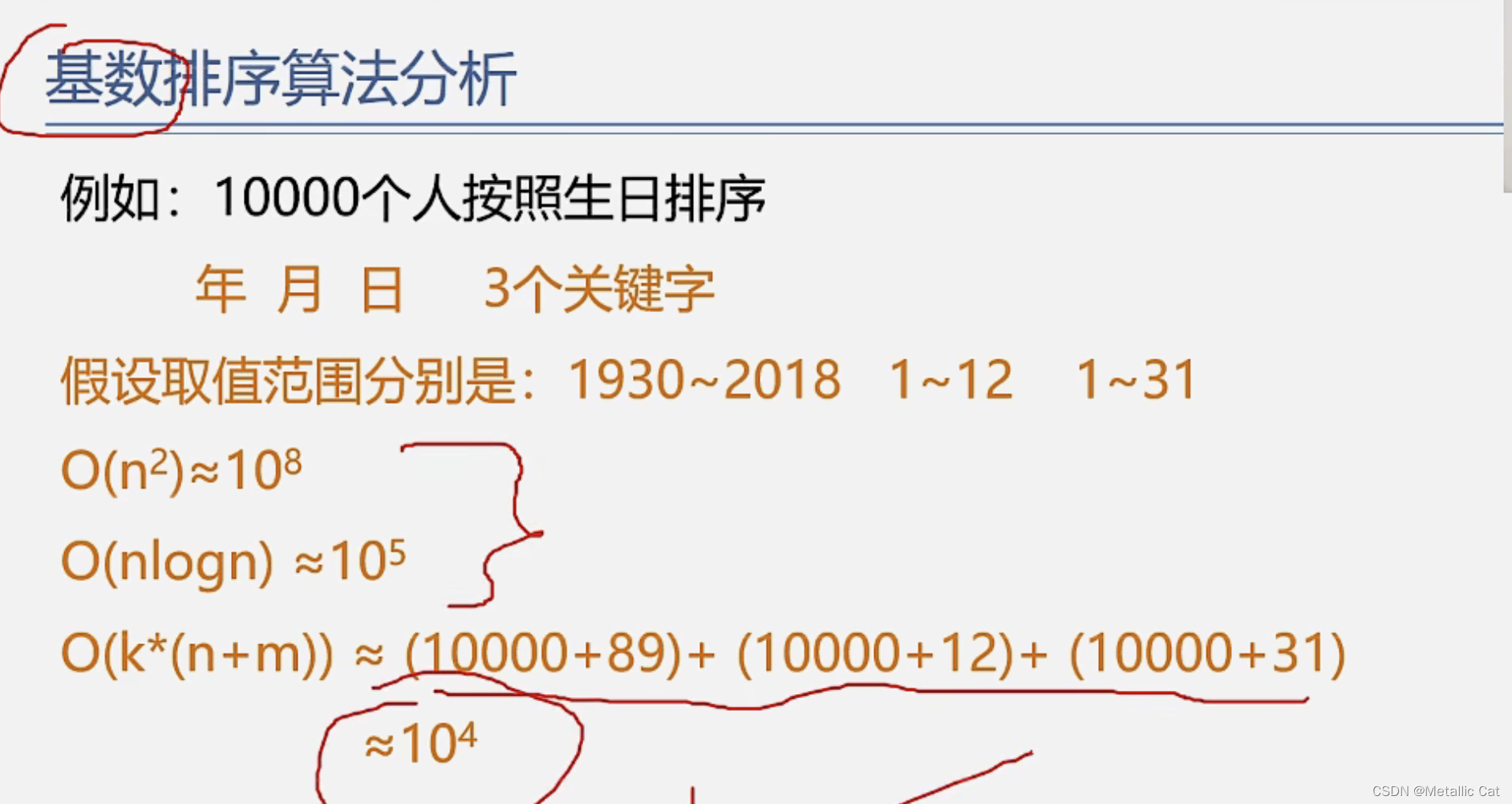
1.m的个数其实就是桶的个数

2.对于一次基数排序而言，如果有k个关键字的话，我们需要进行K次将所有元素分配入桶和K次从桶中收集元素

每一次分配入桶都会对n个元素（所有元素）依次操作，每一次从桶收集都会对m个桶依次操作，则一次基数排序执行的语句总次数为 K*（n+m）次

1.最好的情况就是分配一次和收集一次之后我们就排好序了

第三部分 --- 总结