机器学习笔记第一章绪论

1.1 基本术语

假设收集一批关于西瓜的数据，如（色泽=青绿；根蒂=蜷缩；敲声=浊响）.....这组记录的集合称为一个“数据集”，其中每条记录是关于一个事件或对象的描述，称为一个“示例”或“样本”，反映事件或对象在某方面的表现或性质的事项。属性张成的空间称为“属性空间”、“样本空间”、或“输入空间”。由于空间中的每个点对应一个坐标向量，因此我们也把一个示例称为一个“特征向量”。

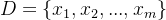
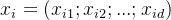
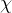
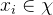
一般地，令 $D=\left \{ x_{1} , x_{2} ,..., x_{m} \right \}$ 表示包含m个示例的数据集，每个示例由d个属性描述，则每个示例 $x_{i}=(x_{i1};x_{i2};...;x_{id})$ 是d维样本空间 $\chi$ 中的一个向量， $x_{i}\in \chi$ ，其中 $x_{ij}$ 是 $x_{i}$ 在第j个属性上的取值，d称为样本 $x_{i}$ 的“维数”。

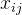
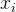
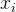
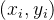
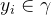
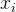
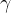
从数据中学的模型的过程称为“学习”或“训练”，这个过程通过执行某个学习算法来完成，训练过程中使用的数据称为“训练数据”，其中每个样本称为一个“训练样本”，训练样本组成的集合称为“训练集”。一般地，用 $(x_{i},y_{i})$ 表示第i个样例，其中 $y_{i}\in \gamma$ 是示例 $x_{i}$ 的标记， $\gamma$ 是所有标记的集合，亦称“标记空间”或“输出空间”。

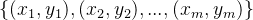
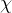
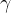
一般地，预测任务是希望通过对训练集 $\left \{ (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m}) \right \}$ 进行学习，建立一个从输入空间 $\chi$ 到输出空间 $\gamma$ 的映射f: $\chi \rightarrow \gamma$ 。学得模型后，使用其进行预测的过程称为“测试”，被预测的样本称为“测试样本”。

“聚类”，即将训练集中的西瓜分成若干组，每组称为一个“簇”。根据训练数据是否拥有标记信息，学习任务可大致划分为两大类：“监督学习”和“无监督学习”，分类和回归是前者的代表，而聚类则是后者的代表。

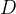
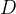
学习模型适用于新样本的能力，称为“泛化”能力，具有强泛化能力的模型能很好地适用于整个样本空间。通常假设样本空间中全体样本服从一个未知“分布”，我们获得的每个样本都是独立地从这个分布上采样获得的，即“独立同分布”。一般而言，训练样本越多，我们得到的关于的信息越多，这样就越有可能通过学习获得具有强泛化能力的模型。

1.2 归纳偏好

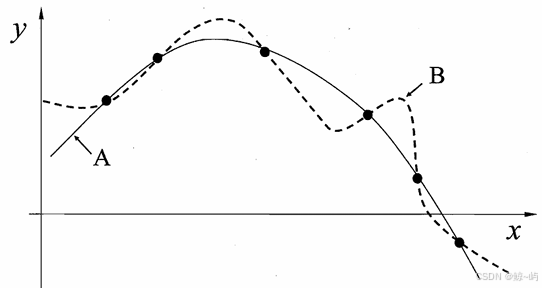
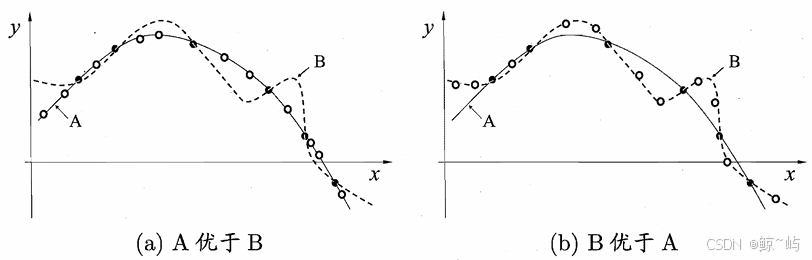
机器学习算法在学习过程中对某种类型假设的偏好，称为"归纳偏好" (inductive bias) , 或简称为"偏好"。任何一个有效的机器学习算法必有其归纳偏好，否则它将被假设空间中看似在训练集上"等效"的假设所迷惑，而无法产生确定的学习结果。归纳偏好的作用在图1.3这个回归学习图示中可能更直观.这里的每个训练样本是因中的一个点 (x，y)，要学得一个与训练集一致的模型，相当于找到一条穿过所有训练样本点的曲线.显然，对有限个样本点组成的训练集，存在着很多条曲线与其一致.我们的学习算法必须有某种偏好，才能产出它认为"正确"的模型。归纳偏好可看作学习算法自身在一个可能很庞大的假设空间中对假设进行选择的启发式或"价值观"。

1.3 NFL定理

事实上，归纳偏好对应了学习算法本身所做出的关于"什么样的模型更好"的假设.在具体的现实问题中，这个假设是否成立，即算法的归纳偏好是否与问题本身匹配，大多数时候直接决定了算法能否取得好的性能。

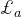
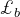
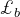
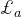
对于一个学习算法 $\pounds _{a}$ ，若它在某些问题上比学习算法 $\pounds _{b}$ 好，则必然存在另一些问题，在那里 $\pounds _{b}$ 比 $\pounds _{a}$ 好，这就称之为NFL定理。NFL定理的重要前提是，所有“问题”出现的机会相同、或所有问题同等重要。实际情形并非如此；我们通常只关注自己正在试图解决的问题。脱离具体问题，空泛地谈论“什么学习算法更好”毫无意义，所以需要具体问题，具体分析。

参考文献：《机器学习》周志华