Magic Numbers: Can Maths Equations Be Beautiful?
神奇的数字 数学方程式也可以很美吗?
Paul Dirac had an eye for beauty. In one essay, from May 1963, the British Nobel laureate referred to beauty nine times. It makes four appearances in four consecutive sentences. In the article he painted a picture of how physicists saw nature. But the word beauty never defined a sunset, nor a flower, or nature in any traditional sense. Dirac was talking quantum theory and gravity. The beauty lay in the mathematics.
保罗-狄拉克有一双发现美的眼睛。在 1963 年 5 月的一篇文章中,这位英国诺贝尔奖得主九次提到美。它在连续的四个句子中出现了四次。在这篇文章中,他描绘了一幅物理学家眼中的大自然。但 “美 ”这个词从来不只被定义在夕阳、花朵或任何传统意义上的自然中。狄拉克说的是量子理论和万有引力。美在于数学。
What does it mean for maths to be beautiful? It is not about the appearance of the symbols on the page. That, at best, is secondary. Maths becomes beautiful through the power and elegance of its arguments and formulae; through the bridges it builds between previously unconnected worlds. When it surprises. For those who learn the language, maths has the same capacity for beauty as art, music, a full blanket of stars on the darkest night.
数学之美意味着什么?这与页面上符号的外观无关。这充其量只是次要的。数学因其论证和公式的力量和优雅而美丽,因其在以前没有联系的世界之间架起的桥梁而美丽。让人惊喜对于那些学习数学语言的人来说,数学与艺术、音乐、漆黑夜晚的满天繁星一样,都具有美的能力。
"The slow movement of the Mozart clarinet concerto is a really beautiful piece of music, but I don’t print off a page of the score and put that on my wall. It’s not about that. It’s about the music and the ideas and the emotional response,〞 says Vicky Neale, a mathematician at Oxford University. “It’s the same with a piece of mathematics. It’s not how it looks, it‘s about the underlying thought processes."
“莫扎特单簧管协奏曲的慢板是一首非常优美的乐曲,但我不会把乐谱打印出来贴在墙上。这与此无关。牛津大学的数学家维姬-尼尔说:"这与音乐、思想和情感反应有关。牛津大学的数学家维基-尼尔说,"数学作品也是如此。这与它的外观无关,而是与潜在的思维过程有关”。
Brain scans of mathematicians show that gazing at formulae considered beautiful by the beholder elicits activity in the same emotional region as great art and music. The more beautiful the formula, the greater the activity in the medial orbito-frontal cortex. “So far as the brain is concerned, maths has beauty just like art. There is common neurophysiological ground," says Sir Michael Atiyah, an honorary professor of mathematics at Edinburgh University.
对数学家进行的大脑扫描显示,凝视被观赏者视为美丽的公式会在与伟大的艺术和音乐相同的情感区域引起活动。公式越美,内侧眶额皮层的活动就越强。爱丁堡大学数学系荣誉教授迈克尔-阿蒂亚爵士说:“就大脑而言,数学与艺术一样具有美感。数学与艺术一样,具有共同的神经生理学基础。”
Ask mathematicians about the most beautiful equation and one crops up time and again. Written in the 18th century by the Swiss mathematician, Leonhard Euler, the relation is short and simple: . It is neat and compact even to the naive eye. But the beauty comes from a deeper understanding: here the five most important mathematical constants are brought together. Euler’s formula marries the world of circles, imaginary numbers and exponentials.
向数学家们询问最美丽的方程,其中一个会被反复提及。这个关系式由瑞士数学家莱昂哈德-欧拉(Leonhard Euler)在 18 世纪写成,简短明了:。但其美妙之处来自更深层次的理解:这里汇集了五个最重要的数学常数。欧拉公式将圆、虚数和指数的世界融为一体。
The beauty of other formulae may be more obvious. With 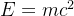
其他公式的魅力可能更为明显。爱因斯坦用 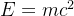
"One of the reasons there’s almost an objective beauty in mathematics is that we use the word beautiful also to indicate the raw power in an idea. The equations or results in mathematics that are seen to be beautiful are almost like poems. The power per variable is something that is part of the experience. Just seeing a huge part of mathematics or nature being described with just a few symbols gives a great sense of elegance or beauty," Dijkgraaf adds. "A second element is you feel its beauty is reflecting reality. It’s reflecting a sense of order that’s out there as part of the laws of nature."
“数学中几乎有一种客观存在的美,原因之一是我们用 “美 ”这个词也是为了表示一种思想的原始力量。数学中被视为美的方程或结果几乎就像一首诗。每个变量的力量是经验的一部分。只需看到数学或自然的一个巨大部分被用几个符号描述出来,就会给人一种非常优雅或美丽的感觉,”迪克格拉夫补充道。“第二个要素是,你会觉得它的美反映了现实。它反映了作为自然法则一部分的秩序感。”
The power of an equation to connect what seem like completely unrelated realms of mathematics comes up often. Marcus du Sautoy, a maths professor at Oxford, has more than a soft spot for Riemann’s formula. Published by Bernhard Riemann in 1859 (the same year Charles Darwin stunned the world with On the Origin of Species), the formula reveals how many primes exist below a given number, where primes are whole numbers divisible only by themselves and one, such as 2, 3, 5, 7 and 11. While one side of the equation describes the primes, the other is controlled by zeros.
一个等式能把看似完全不相关的数学领域联系起来,这种力量经常出现。牛津大学数学教授马库斯-杜索伊对黎曼公式情有独钟。黎曼公式由伯恩哈德-黎曼(Bernhard Riemann)于 1859 年发表(同年,查尔斯-达尔文发表了震惊世界的《物种起源》),该公式揭示了一个给定数字下面存在多少个素数,素数是指只能被自己和 1 整除的整数,如 2、3、5、7 和 11。等式的一边描述了素数,另一边则由零控制。
"This formula turns these these indivisible prime numbers, into something completely different," says du Sautoy. "On the one side, you’ve got these indivisible prime numbers and then Riemann takes you on this journey to somewhere completely unexpected, to these things which we now call the Riemann zeros. Each of these zeros gives rise to a note – and it’s the combination of these notes together which tell us how the primes on the other side are distributed across all numbers."
杜索伊说:“这个公式把这些不可分割的素数变成了完全不同的东西。一方面,你得到了这些不可分割的质数,然后黎曼带你到一个完全意想不到的地方,我们现在称之为黎曼零点。每一个零都会产生一个音符,而这些音符的组合就会告诉我们 另一边的素数是如何在所有数字中分布的。”
More than 2,000 years ago, the ancient Greek mathematician, Euclid, solved a numerical puzzle so beautifully that it still makes Neale smile every time it comes to mind. "When I think about beauty in mathematics, my first thoughts are not about equations. For me it’s much more about an argument, a line of thinking, or a particular proof," she says.
两千多年前,古希腊数学家欧几里得解决了一道数字难题,其解题过程之美,至今仍让尼尔每次想起都会会心一笑。她说:“当我想到数学之美时,我首先想到的不是方程式。对我来说,更多的是关于一个论点、一个思路或一个特定的证明。”
Euclid proved there are infinitely many prime numbers. How did he do it? He began by imagining a universe where the number of primes was not infinite. Given a big enough blackboard, one could chalk them all up.
欧几里得证明了有无穷多个素数。他是怎么做到的呢?他首先想象了一个素数并非无限的宇宙。如果有一块足够大的黑板,人们可以用粉笔把它们都写出来。
He then asked what happened if all these primes were multiplied together: 2 x 3 x 5 and so on, all the way to the end of the list, and the result added to the number 1. This huge new number provides the answer. Either it is a prime number itself, and so the original list was incomplete, or it is divisible by a smaller prime. But divide Euclid’s number by any prime on the list and always there is a 1 left over. The number is not divisible by any prime on the list. "It turns out you reach an absurdity, a contradiction," says Neale. The original assumption that the number of primes is finite must be wrong.
然后他又问,如果把所有这些素数相乘会怎样:2 x 3 x 5,依此类推,一直到列表的最后,然后把结果加到数字 1 上。这个巨大的新数字给出了答案。要么它本身就是一个质数,所以原来的列表并不完整,要么它能被一个更小的质数整除。但是,欧几里得数除以列表中的任何素数,总会剩下一个 1。这个数不能被列表中的任何素数整除。尼尔说:“事实证明,你得出了一个荒谬的结论,一个矛盾的结论。原来关于素数是有限的假设肯定是错误的。”
"The proof for me is really beautiful. It takes some thinking to get your head around it, but it doesn’t involve learning lots of difficult concepts. It’s surprising that you can prove something so difficult in such an elegant way," Neale adds.
“对我来说,证明真的很美。你需要花一些时间去思考,但这并不涉及学习很多困难的概念。你能以如此优雅的方式证明如此困难的事情,真是令人惊讶。”尼尔补充道。
Behind beautiful processes lie beautiful mathematics. Well, some of the time. Hannah Fry, a lecturer in the mathematics of cities at UCL spent years staring at the Navier-Stokes equations. "They’re a single mathematical sentence that is capable of describing the miraculously beautiful and diverse behaviour of almost all of Earth’s fluids," she says. With a grasp of the formulae, we can understand blood flow in the body, make boats glide through the water, and build awesome chocolate enrobers.
美丽的过程背后是美丽的数学。嗯,有些时候是这样。伦敦大学洛杉矶分校城市数学讲师汉娜-弗莱(Hannah Fry)多年来一直在研究纳维-斯托克斯方程。她说:“它们是一个数学句子,能够描述地球上几乎所有流体奇迹般地美丽而多样的行为。掌握了这些公式,我们就能理解人体中的血液流动,让船只在水中滑行,并制造出令人惊叹的巧克力灌装机。”
In his 1963 essay, Dirac elevated beauty from an aesthetic response to something far more profound: a route to the truth. "It is more important to have beauty in one’s equations than to have them fit experiment," he wrote, continuing: "It seems that if one is working from the point of view of getting beauty in one’s equations, and if one has really a sound insight, one is on a sure line of progress." Shocking at first pass, Dirac captured what is now a common sentiment: when a beautiful equation seems at odds with nature, the fault may lie not with the maths, but in applying it to the wrong aspect of nature.
在 1963 年的文章中,狄拉克将美从审美反应提升到了更深远的意义:通往真理的途径。他写道:“让方程具有美感比让方程符合实验更为重要,他继续写道:“看来,如果一个人从在方程中体现美感的角度出发,如果一个人真的有正确的洞察力,那么他就一定会取得进步。”一语惊人,狄拉克捕捉到了现在人们的普遍感受:当一个美丽的方程似乎与自然相悖时,错误可能不在于数学,而在于把数学应用到了自然的错误方面。
"Truth and beauty are closely related but not the same," says Atiyah. "You are never sure that you have the truth. All you are doing is striving towards better and better truths and the light that guides you is beauty. Beauty is the torch you hold up and follow in the belief that it will lead you to truth in the end."
阿提亚说:“真理和美是密切相关的,但又不尽相同。”你永远无法确定自己是否掌握了真理。你所做的一切都是为了更好的真理而努力,而指引你的光就是美。美是你高举和追随的火炬,相信它最终会指引你找到真理。
Something approaching faith in mathematical beauty has led physicists to draw up two of the most compelling descriptions of reality: supersymmetry and string theory. In a supersymmetric universe, every known type of particle has a heavier, invisible twin. In string theory, reality has 10 dimensions, but six are curled up so tight they are hidden from us. The mathematics behind both theories are often described as beautiful, but it is not at all clear if either is true.
对数学之美的近乎信仰,促使物理学家对现实做出了两种最有说服力的描述:超对称和弦理论。在超对称宇宙中,每一种已知的粒子都有一个更重的隐形孪生兄弟。在弦理论中,现实有 10 个维度,但其中 6 个维度蜷缩得很紧,不为我们所知。这两种理论背后的数学常常被描述为美轮美奂,但其中任何一种理论是否属实却并不清楚。
There is a danger here for mathematicians. Beauty is a fallible guide. "You can literally be seduced by something that is not correct. This is a risk," says Dijkgraaf, whose institute motto, "Truth and Beauty" features one naked and one dressed woman. “Sometimes I feel that physicists, like Odysseus, must tie themselves to the mast of the ship so they are not seduced by the sirens of mathematics."
对于数学家来说,这里存在着危险。美是一种易错的指导。迪克格拉夫说:"你可能真的会被不正确的东西所诱惑。这是一种风险,“迪克格拉夫说,他的研究所座右铭“真理与美”的图案是一个裸体女人和一个着装女人。”有时我觉得物理学家就像奥德修斯一样,必须把自己绑在船桅上,这样他们才不会被数学女妖所诱惑。
It may be that mathematicians and scientists are the only groups that still use the word "beautiful" without hesitation. It is rarely employed by critics of literature, art or music, who perhaps fear it sounds superficial or kitschy.
数学家和科学家可能是唯一仍在毫不犹豫地使用 “美丽 ”一词的群体。文学、艺术或音乐评论家很少使用“美”这个字,也许他们担心这个字听起来肤浅或俗气。
"I’m very proud that in mathematics and science the concept of beauty is still there. I think it’s an incredibly important concept in our lives," says Dijkgraaf. "The sense of beauty we experience in maths and science is a multidimensional sense of beauty. We don’t feel it’s in any conflict with being deep, or interesting, or powerful, or meaningful. For the mathematician it’s all captured by that one word."
我为数学和科学中仍然存在“美”的概念而感到自豪。我认为这是我们生活中一个非常重要的概念,"迪克格拉夫说。“我们在数学和科学中体验到的美感是一种多维度的美感。我们不觉得它与深刻、有趣、强大或有意义有任何冲突。对于数学家来说,这一切都可以用一个词来概括"。