Day38
322. 零钱兑换
思路
完全背包
代码
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int i = 0; i < coins.size(); i++) { // 遍历物品
for (int j = coins[i]; j <= amount; j++) { // 遍历背包
if (dp[j - coins[i]] != INT_MAX) { // 如果dp[j - coins[i]]是初始值则跳过
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
}
}
}
if (dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};
五部曲
1.dp数组及下标定义:凑足金额j所需钱币的最小个数
2.递推公式:dp[j] = min( dp[j - coins[i]] + 1, dp[j] )
3.初始化:dp[0] = 0; 其余数组初始化为INT_MAX
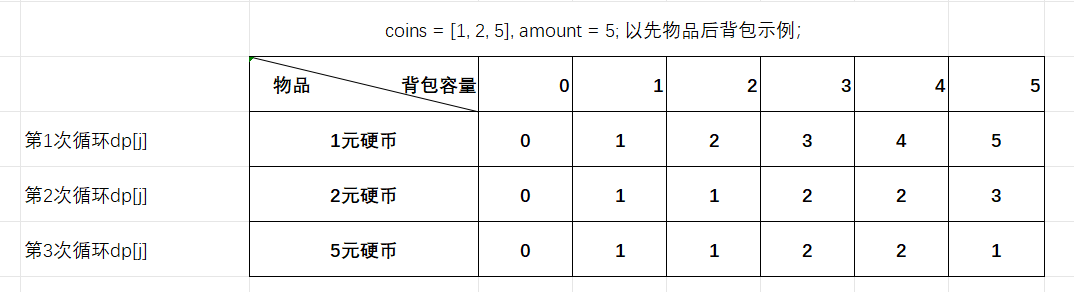
4.遍历顺序:钱币有顺序和无顺序都可以,不影响最终结果,所以内外层循环可以先物品,后背包;也可以先背包,后物品。
5.数组的数据应该是怎样的:
思考
一、代码中为什么有这样一句“if (dp[j - coins[i]] != INT_MAX)”
dp[j - coins[i]] 的值为 INT_MAX 时,表示无法用当前硬币组合出金额 j - coins[i]。此时若强行进行 dp[j - coins[i]] + 1 的计算,会导致整数溢出(例如 INT_MAX + 1 会变成负数)。
二、
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。