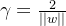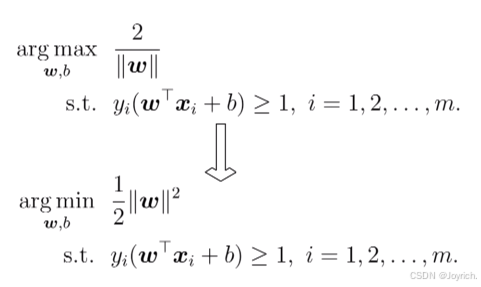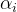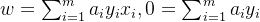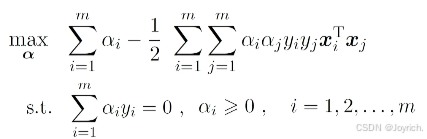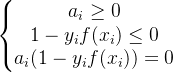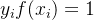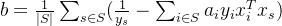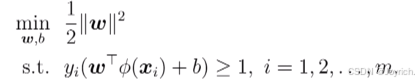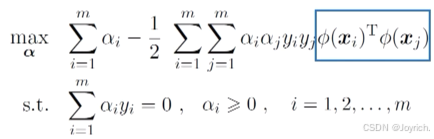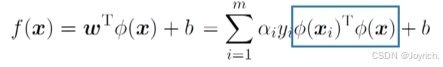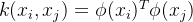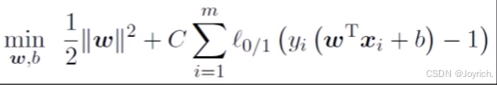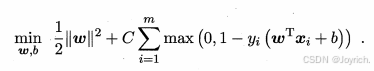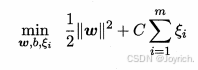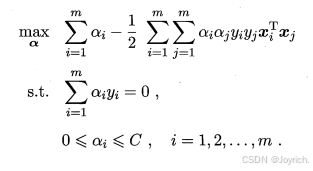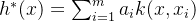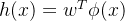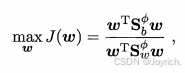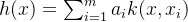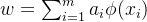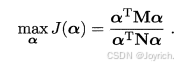目录
6.1 间隔与支持向量
分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面,将不同类别的样本分开.但能将训练样本分开的划分超平面可能有很多,如下图所示
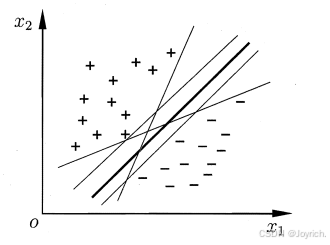
“正中间”的:鲁棒性最好,泛化能力最强
超平面方程:
样本空间中任意点到超平面(w,b)的距离可写为:
如图6..1.2所示,距离超平面最近的这几个训练样本点点到超平面的距离为1,它们被称为“支持向量”(support vector),两个异类支持向量到超平面的距离之和为:
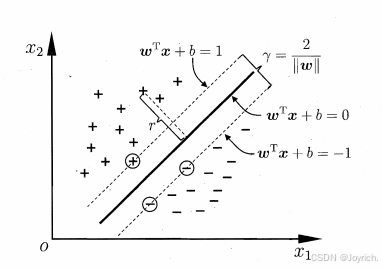
现在我们需要找到最大间隔的划分超平面,使y最大
6.2 对偶问题
支持向量机本身是一个二次规划问题,能用优化计算包求解,但可以有更高效的办法
拉格朗日乘子法:
- 第一步:引入拉格朗日乘子法
0得到拉格朗日函数:
- 第二步:令L(w,b,a)对w和b的偏导为零可得:
- 第三步:回代可得:
最终模型:
需要满足KKT条件:
必有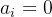
- 解的稀疏性:
训练完成后,最终模型仅与支持向量有关
这个解法还不够方便,还有更容易的方法:
- SMO:
基本思路:不断执行如下两个步骤直至收敛
- 第一步: 选取一对需更新的变量
和
- 第二步: 固定
和
以外的参数,求解对偶问题更新
和
仅考虑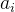
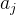

用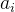
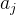
对任意支持向量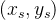
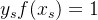
但现实任务中常采用一种更鲁棒的做法:使用所有支持向量求解的平均值
6.3 核函数
若不存在一个能正确划分两类样本的超平面,怎么办?
将样本从原始空间映射到一个更高维的特征空间,使样本在这个特征空间内线性可分

如果原始空间是有限维(属性数有限),那么—定存在一个高维特征空间使样本线性可分
- 原始问题:
- 对偶问题:
- 预测:
计算高维的内积非常困难,所以我们设想了一个函数(核函数):
绕过显式考虑特征映射、以及计算高维内积的困难
Mercer定理: 若一个对称函数所对应的核矩阵半正定,则它就能作为核函数来使用
任何一个核函数,都隐式地定义了一个RKHS(Reproducing Kernel HilbertSpace,再生核希尔伯特空间)
“核函数选择”成为决定支持向量机性能的关键!
6.4 软间隔与正则化
6.4.1 软间隔
现实中很难确定合适的核函数。使训练样本在特征空间中线性可分,即便貌似线性可分,也很难断定是否是因过拟合造成的
引入软间隔(Soft Margin),允许在一些样本上不满足约束

基本思路: 最大化间隔的同时,让不满足约束≥1的样本尽可能少
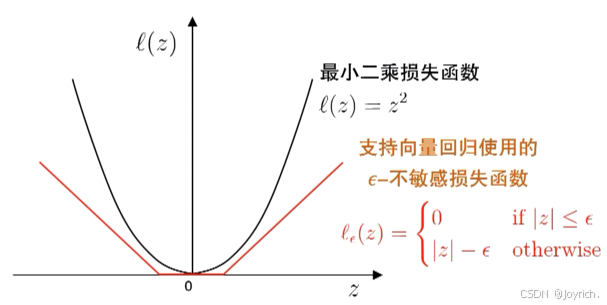
障碍:0/1损失函数非凸、非连续、不易优化!
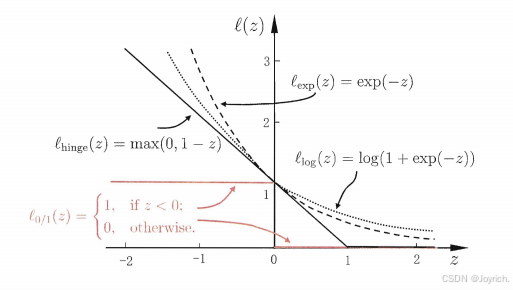
- 采用替代损失函数,是在解决困难问题时的常见技巧
- 求解替代函数得到的解是否仍是原问题的解?理论上称为替代损失的“—致性”(Consistency)问题
软间隔支持向量机:
- 原始问题:
- 引入”松弛量“:
- 对偶问题:
根据KKT条件可知,最终模型仅与支持向量有关,也即采用hinge损失函数后仍保持了sVM解的稀疏性
6.4.2 正则化
统计学习模型的更一般形式:
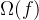
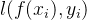
- 正则化可理解为“罚函数法”
- 通过对不希望的结果施以惩罚,使得优化过程趋向于希望目标从贝叶斯估计的角度,则可认为是提供了模型的先验概率
6.5 支持向量回归
基本思路:允许模型输出与实际输出间存在2
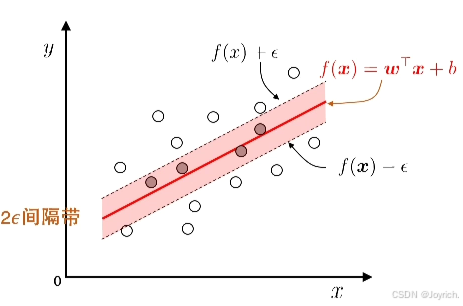
落入2
- 原始问题:
- 对偶问题:
- 预测:
6.6 核方法
- 表示定理:
令H为核函数k对应的再生核希尔伯特空间,优化问题:
解为:
对于一般的损失函数和正则化项,优化问题的最优解h*(z)都可表示为核函数的线性组合
核方法:核函数的学习方法
- 核化:
将线性学习器拓展为非线性学习器,从而得到“核线性判别分析”
通过某种映射将样本映射到一个特征空间,然后进行线性判别分析,求得:
KLDA学习目标:
用核函数来替代高维的内积,
可得:
最后KLDA学习目标可等价为: