最大堆
每个结点的值都大于或等于其左右孩子结点的值
如上图,将数组ar抽象构建成一棵完全二叉树,若每个节点的值都大于其左右孩子节点 ,则该完全二叉树为最大堆。
最小堆
每个结点的值都小于或等于其左右孩子结点的值
算法思想
- 将数组构建成一棵完全二叉树
- 将构建的完全二叉树从下到上遍历,使其成为最大堆
- 此时,整个序列的最大值就是堆顶的根节点。
- 将其与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
动图演示
静态分解
int ar[]={37,53,35,23,30,48,25,11}; //对此数组分析
当我们将一个由数组构建的完全二叉树调整为最大堆时,发现根节点为数组中最大值,所以可以用这种方式将每一轮的最大值依次放入数组尾部,从而实现将无序数组重新按由小到大的顺序排列。
代码实现:
1.实现了对一个堆的一个节点进行调整,以满足大根堆的要求
//实现了对一个堆的一个节点进行调整,以满足最大堆的要求
void FliterDown(int* heap,const int start,const int end)
{
assert(heap != NULL);
int i = start; //i为当前根节点
int j = 2*i + 1; //j为左孩子节点
int tem = heap[i];
while(j <= end)
{
if(j < end && heap[j] < heap[j+1]) j++; //比较左右孩子节点大小
if(tem >= heap[j]) break; //满足要求跳出
heap[i] = heap[j]; //不满足要求,更新当前根节点值
i = j; //更新根节点
j = j*2 + 1; //更新作孩子节点
}
heap[i] = tem; //更新当前节点值
}后续对每个非叶子节点依次进行判断调整,即可得到最大堆。
int pos = (n - 2)/2 ; //从最后一个非叶子节点开始,依次对每个节点进行一次 FliterDown操作
//因为堆是一颗完全二叉树,最后一个非叶子节点的位置为 (n-2)/2
while(pos >= 0)
{
FliterDown(arr,pos,n-1);
pos--;
}将最大堆的根节点和数组的最后一个数据进行交换,然后数组前 n-1 个数据再次进行最大堆调整,再次交换,以此类推,即可得到最终从小到大排序的数据。
for(int i = n-1;i > 0;i--)
{
FliterDown(arr,0,i);
Swap(&arr[0],&arr[i]); //利用自定义交换函数实现每一轮最大值后移
} 总体代码:
#include<stdio.h>
#include<assert.h>
void Swap(int* a,int* b)
{
assert(a!= NULL && b !=NULL);
int c = *a;
*a = *b;
*b = c;
}
//最大堆
void Swap(int* a,int* b);
void FliterDown(int* heap,const int start,const int end) //单次排序
{
assert(heap != NULL);
int i = start;
int j = 2*i + 1;
int tem = heap[i];
while(j <= end)
{
if(j < end && heap[j] < heap[j+1]) j++;
if(tem >= heap[j]) break;
heap[i] = heap[j];
i = j;
j = j*2 + 1;
}
heap[i] = tem;
}
void FliterSort(int* arr,int n)
{
assert(arr != NULL);
int pos = (n - 2)/2 ;
while(pos >= 0)
{
FliterDown(arr,pos,n-1);
pos--;
}
for(int i = n-1;i > 0;i--)
{
FliterDown(arr,0,i);
Swap(&arr[0],&arr[i]);
}
}
void print(int *arr,int len)
{
assert(arr != NULL);
for(int i=0 ;i<len;i++)
{
printf("%d ",arr[i]);
}
printf("\n");
}
int main()
{
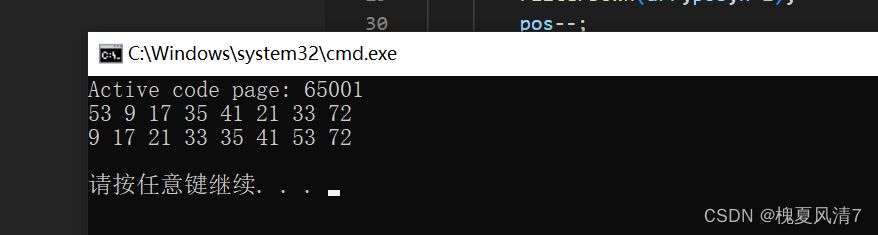
int ar[]= {53,9,17,35,41,21,33,72};
int len = sizeof(ar)/sizeof(ar[0]);
print(ar,len);
FliterSort(ar,len);
print(ar,len);
}测试结果:
时间复杂度
堆排序的是将数组构建成最小堆或者最大堆的方式,对数据进行排序,其时间复杂度为O(nlog n);