目录

一、聚类的原理与实现

1.1 聚类的概念和类型

1.2 如何度量距离

1.2.1 数据的类型

1.2.2 连续型数据的距离度量方法

1.2.3 离散型数据的距离度量方法

1.3 聚类的基本步骤

二、层次聚类算法

2.1 算法原理和实例

2.2 算法的Sklearn实现

2.2.1 层次聚类法的可视化实例

2.2.2 绘制层次聚类的树状图

2.2.3 DataFrame数据结构

三、k-means聚类算法

3.1 算法原理和实例

3.1.1 k-means聚类算法原理

3.1.2 k-means聚类算法举例

3.1.3 k-means聚类算法的优缺点

3.2 算法中k值的确定

3.3 算法的Sklearn实现

一、聚类的原理与实现

1.1 聚类的概念和类型

聚类是一种无监督学习的方法，用于将数据集中的对象按照它们的相似性分组。聚类的目标是使得同一组内的对象之间的相似性尽可能地高，而不同组之间的相似性尽可能地低。

聚类的类型包括：

1. 划分聚类（Partitioning Clustering）：将数据集划分成不重叠的子集，每个子集代表一个聚类。常见的划分聚类算法包括K均值聚类和K均值++聚类。

2. 层次聚类（Hierarchical Clustering）：将数据集组织成一个层次结构，每个层次上的节点代表一个聚类。层次聚类可分为自底向上的凝聚聚类和自顶向下的分裂聚类。

3. 密度聚类（Density-based Clustering）：根据数据点的密度将数据集划分为聚类。具有相对较高密度的数据点将组成聚类，而低密度区域将被认为是噪声。DBSCAN是一种常用的密度聚类算法。

4. 基于模型的聚类（Model-based Clustering）：假设数据集由多个潜在的概率模型组成，每个模型代表一个聚类。常见的基于模型的聚类算法包括高斯混合模型聚类（GMM）和期望最大化（EM）算法。

5. 网络聚类（Network Clustering）：用于处理图数据的聚类方法。它将图中的节点分组成聚类，使得聚类内部的节点紧密相连，而不同聚类之间的连接较少。社区发现是网络聚类的一种典型应用。

1.2 如何度量距离

1.2.1 数据的类型

数据可以根据其类型进行分类，主要分为离散型数据和连续型数据。

离散型数据是指在一定范围内，只能取有限个或者可数个数值的数据。离散型数据通常代表了非可度量的特征或者属性。例如，一个学生的成绩可以用A、B、C等等来表示，或者一个人的血型可以用A、B、O、AB来表示。

离散型数据还可以分为定类数据、定序数据、定距数据。

1. 定类数据是指数据按照某种特征或属性进行分类，但不存在相对大小的关系，例如性别（男、女）、民族（汉族、藏族、维吾尔族等）。
2. 定序数据是指数据可以按照某种特征或属性进行分类，并且存在相对大小的关系，例如教育程度（小学、初中、高中、大学）或荣誉等级（一等奖、二等奖、三等奖）。
3. 定距数据是指数据可以按照某种特征或属性进行分类，存在相对大小的关系，并且可以进行加减运算，但没有绝对零点，例如温度（摄氏度、华氏度）或年龄。

连续型数据是指在一定范围内可以取任意值的数据。连续型数据通常代表了可度量的特征或者属性。例如，一个人的身高可以是任意的数值，例如160cm、165.5cm、170cm等等。

对于离散型数据，通常使用频数和百分比来描述和分析数据的分布情况；对于连续型数据，可以使用平均值、中位数、标准差等统计指标来描述和分析数据的分布情况。

1.2.2 连续型数据的距离度量方法

在连续型数据的距离度量方法中，常用的方法有以下几种：

1. 欧氏距离（Euclidean distance）：欧氏距离是最常用的距离度量方法，它计算两个样本之间的直线距离。对于两个样本点 (x1, y1) 和 (x2, y2)，欧氏距离可以表示为：d = sqrt((x2 - x1)^2 + (y2 - y1)^2)

2. 曼哈顿距离（Manhattan distance）：曼哈顿距离是计算两点之间的距离，沿着网格线的距离，而不是直线距离。对于两个样本点 (x1, y1) 和 (x2, y2)，曼哈顿距离可以表示为：d = |x2 - x1| + |y2 - y1|

3. 切比雪夫距离（Chebyshev distance）：切比雪夫距离是计算两点之间的最大差距，即两点坐标轴方向上差值的最大值。对于两个样本点 (x1, y1) 和 (x2, y2)，切比雪夫距离可以表示为：d = max(|x2 - x1|, |y2 - y1|)

4. 闵可夫斯基距离（Minkowski distance）：闵可夫斯基距离是欧氏距离和曼哈顿距离的推广，可以根据需要选择不同的参数。对于两个样本点 (x1, y1) 和 (x2, y2)，闵可夫斯基距离可以表示为：d = (|x2 - x1|^p + |y2 - y1|^p)^(1/p)，其中 p 是一个参数，当 p=1 时为曼哈顿距离，当 p=2 时为欧氏距离。

5. 马氏距离（Mahalanobis distance）：马氏距离是一种考虑各个维度之间相关性的距离度量方法，它通过协方差矩阵来衡量变量之间的相关性。对于两个样本点 x 和 y，马氏距离可以表示为：d = sqrt((x - y)^T Σ^(-1) (x - y))，其中 Σ 是样本的协方差矩阵。

1.2.3 离散型数据的距离度量方法

对于离散型数据的距离度量方法：

1. 简单匹配系数（Simple Matching Coefficient）：适用于两个等长的二进制字符串，定义为两个字符串中相同位置上相同字符的个数除以字符串的长度。

2. 杰卡德相似系数（Jaccard Similarity Coefficient）：适用于表示集合的离散型数据，定义为两个集合交集的大小除以并集的大小。

这两种方法主要适用于二进制字符串和集合类型的离散型数据，用于度量不同数据之间的相似性或距离。

1.3 聚类的基本步骤

对案例进行聚类分析的基本步骤可以如下：

1. 收集数据：收集相关的案例数据，这些数据可以是文本、数字或其他形式的信息。

2. 数据预处理：对收集到的数据进行预处理，包括数据清洗、特征选择、特征缩放等。确保数据的准确性和一致性。

3. 选择聚类算法：根据案例的特征和目标，选择适合的聚类算法。常见的聚类算法包括K均值聚类、层次聚类、DBSCAN等。

4. 确定聚类的数量：如果聚类的数量未知，需要通过一些方法来确定合适的聚类数量。常用的方法包括肘部法则、轮廓系数等。

5. 运行聚类算法：根据选定的聚类算法和确定的聚类数量，运行聚类算法对案例数据进行聚类分析。

6. 评估聚类结果：使用合适的指标评估聚类结果的质量和准确性。常用的评估指标包括轮廓系数、DBI指数等。

7. 可视化和解释结果：将聚类结果可视化，帮助理解和解释聚类结果。可以使用散点图、热力图等方式展示聚类效果，并根据结果解释案例分组的特征和关系。

使用Python进行聚类分析简单示例：

# 导入必要的库
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 生成示例数据
data = {
    'age': [23, 30, 45, 18, 50, 28, 35, 40, 20, 33],
    'score': [85, 92, 78, 88, 95, 83, 87, 80, 85, 89]
}

df = pd.DataFrame(data)

# 数据预处理
X = df[['age', 'score']]

# 设置聚类数量为2
k = 2

# 运行K均值聚类算法
kmeans = KMeans(n_clusters=k)
kmeans.fit(X)

# 获取聚类结果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_

# 可视化聚类结果
fig, ax = plt.subplots()
for i in range(k):
    cluster_points = X[labels == i]
    ax.scatter(cluster_points['age'], cluster_points['score'], label='Cluster {}'.format(i+1))

ax.scatter(centroids[:, 0], centroids[:, 1], marker='x', color='black', label='Centroids')
ax.set_xlabel('Age')
ax.set_ylabel('Score')
ax.legend()
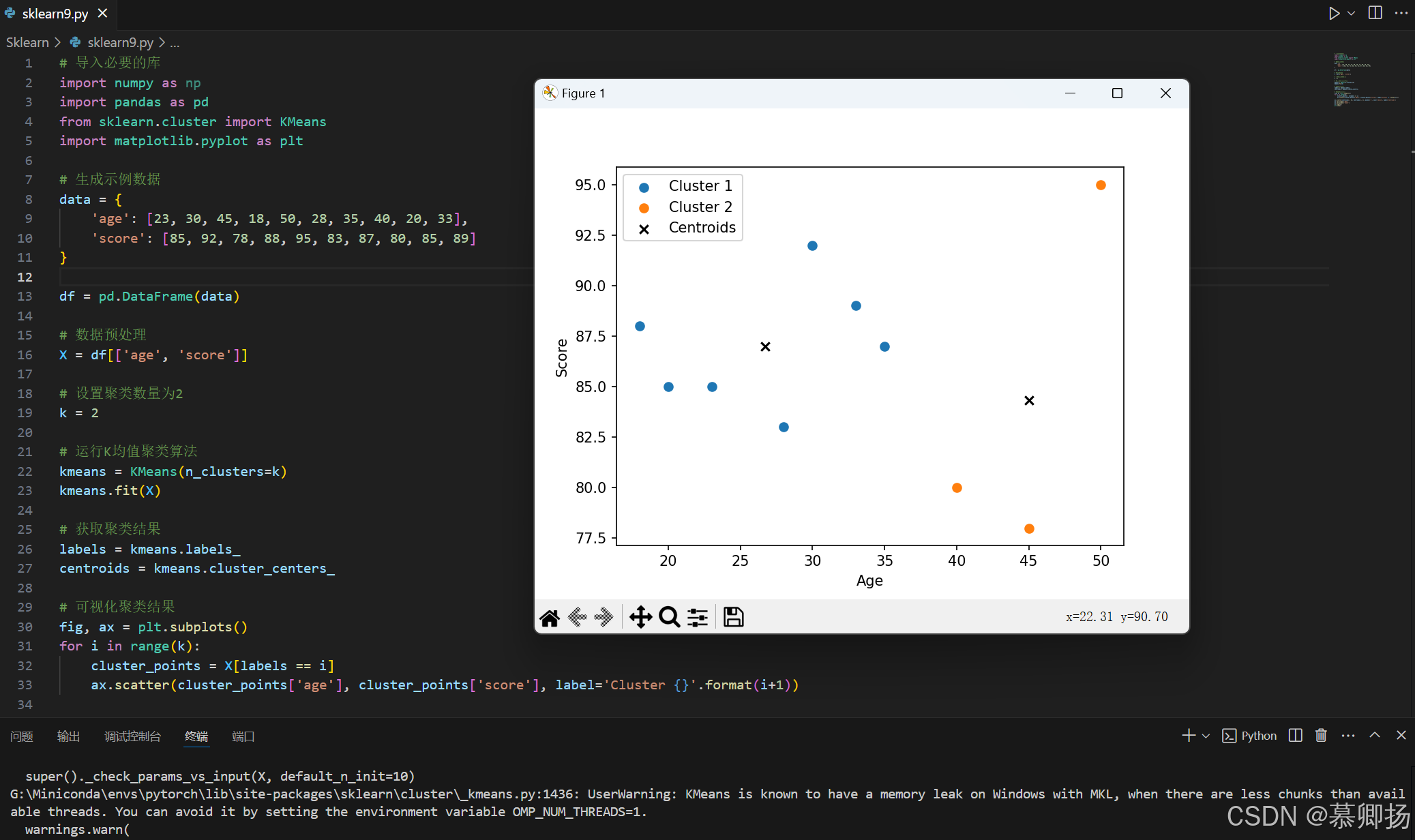
plt.show()

运行结果：

我们使用了pandas库来处理数据，sklearn库中的KMeans类来进行聚类分析，matplotlib库用于可视化聚类结果。

我们首先生成了一个包含年龄和成绩的示例数据集，并进行了数据预处理。然后设置聚类数量为2，并运行K均值聚类算法。最后，通过散点图可视化聚类结果，其中每个群组用不同的颜色表示，并用“x”表示质心。

二、层次聚类算法

层次聚类法（Hierarchical Clustering）是一种将数据分层次进行聚类的方法。它通过不断合并或划分数据来构建一个层次化的聚类结构。层次聚类法可以分为凝聚法（自底向上）和分裂法（自顶向下）两种类型。

凝聚层次聚类是自底向上的方法，它从每个样本作为一个独立的簇开始，然后迭代地将最相似的簇合并在一起，直到所有样本都属于同一个簇。

分裂层次聚类是自顶向下的方法，它从所有样本作为一个簇开始，然后迭代地将最不相似的簇分裂为更小的簇，直到每个样本都作为一个独立的簇。

2.1 算法原理和实例

目前，常见的层次聚类法是凝聚法。凝聚法的原理基于以下几个步骤：

1. 初始化每个样本为一个独立的簇：将每个样本视为一个独立的簇，并计算它们之间的距离或相似度。

2. 计算簇之间的相似度/距离：对于每一对簇，计算它们之间的距离或相似度。常用的距离度量有欧氏距离、曼哈顿距离等，常用的相似度度量有余弦相似度、相关系数等。

3. 合并最相似的簇：选择相似度/距离最小的两个簇进行合并，形成一个新的簇。合并的方式可以是简单地将两个簇合并为一个新的簇，也可以是采用更复杂的方法，如加权平均。

4. 更新簇之间的相似度/距离：更新合并后的簇与其他簇之间的距离或相似度。常用的更新方式有单连接、完全连接和平均连接。

5. 重复步骤3和4：重复进行步骤3和4，直到满足停止条件。停止条件可以是指定的簇的数量，或者是某个相似度/距离的阈值。

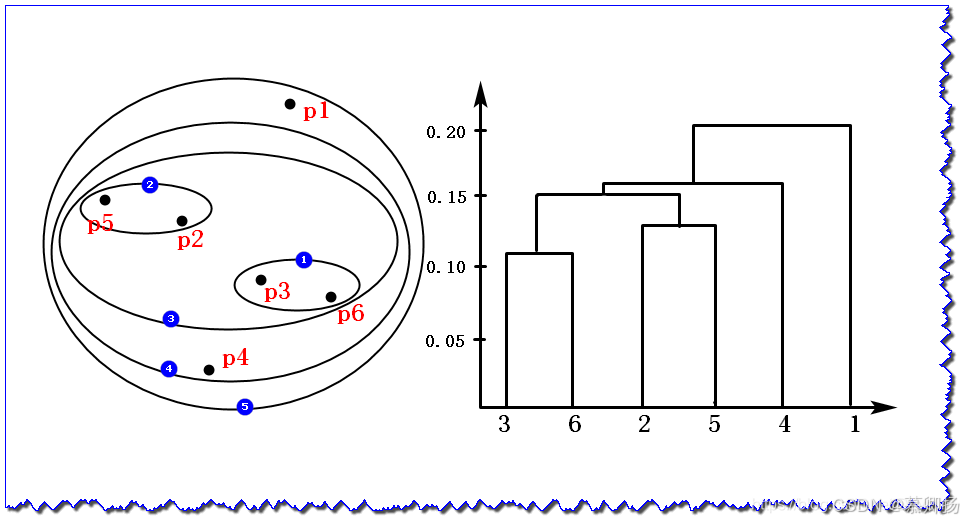
6. 得到最终的聚类结果：最终的聚类结果可以通过截取聚类树状图（树状图中的横轴表示样本，纵轴表示距离/相似度），或者根据停止条件在聚类树中截取簇。

2.2 算法的Sklearn实现

Scikit-learn的聚类模块sklearn.cluster中提供了AgglomerativeClustering类，用来实现层次聚类。该类基于自底向上的聚合策略，先将每个样本视为一个初始单独的簇，然后反复将最相似的两个簇合并，直到满足指定的聚类数量。

AgglomerativeClustering类有多个参数可以调整，包括：

• n_clusters：指定聚类的数量。
• affinity：指定计算样本间距离的度量方法，如欧氏距离、曼哈顿距离等。
• linkage：指定计算合并簇的方式，如单链接(single linkage)、完全链接(complete linkage)等。

AgglomerativeClustering类提供了以下主要方法：

• fit(X)：用于对给定的数据集X进行聚类。
• fit_predict(X)：先对数据集X进行聚类，然后返回每个样本所属的簇标签。
• fit_transform(X)：先对数据集X进行聚类，然后返回每个样本与其他簇的距离。

示例代码如下所示：

from sklearn.cluster import AgglomerativeClustering

# 创建一个AgglomerativeClustering对象
clustering = AgglomerativeClustering(n_clusters=2)

# 对数据集进行聚类
clustering.fit(X)

# 返回每个样本所属的簇标签
labels = clustering.labels_

2.2.1 层次聚类法的可视化实例

使用层次聚类法将样本数据聚成3类，其中样本数据保存在文件km.txt中。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
X1,X2=[],[]
fr=open('Sklearn\km.txt')        # 打开数据文件

for line in fr.readlines():
    lineArr=line.strip().split()
    X1.append([int(lineArr[0])])        # 第1列读取到X1中
    X2.append([int(lineArr[1])])

# 把X1和X2合成一个有两列的数组X并调整维度，此处X的维度为[10,2]
X=np.array(list(zip(X1, X2))).reshape (len(X1), 2)
# print(X)        # X的值为［[21][1 2] [2 2]…[5 3]]
# model=AgglomerativeClustering(3).fit(X)

model=AgglomerativeClustering(n_clusters=3)        # 设置聚类数目为3
labels=model.fit_predict(X)
print(labels)

colors=['b','g','r','c']
markers=['o','s','<','v']
plt.axis([0,6,0,6])
for i,l in enumerate (model.labels_):
    plt.plot(X1[i],X2[i],color=colors[1],marker=markers[1],ls='None')
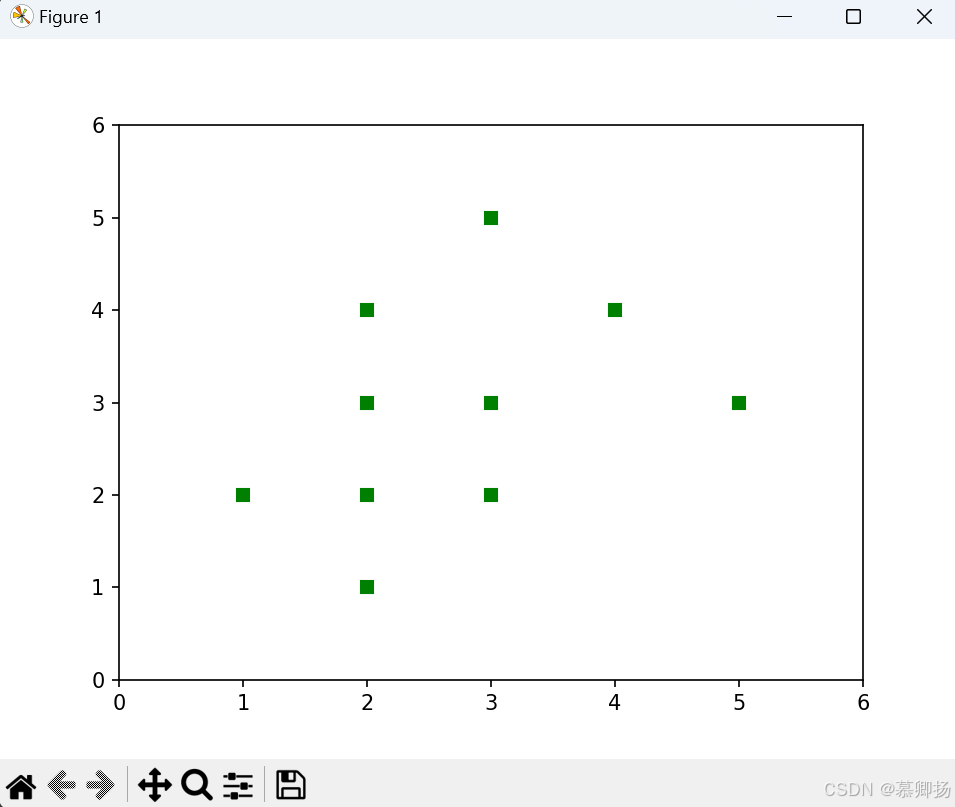
plt.show()

运行结果：

[2221111000]

2.2.2 绘制层次聚类的树状图

scipy.cluster.hierarchy是SciPy中用于聚类分析的层次聚类方法的模块。它提供了一些功能来计算层次聚类和绘制聚类树状图。

scipy.cluster.hierarchy模块提供了以下方法：

1. linkage：计算聚类算法中的连结矩阵。它接受一个距离矩阵作为输入，并返回一个连结矩阵，用于层次聚类。

2. fcluster：根据层次聚类的结果和给定的阈值，对样本进行聚类标记。它接受一个连结矩阵和一个阈值作为输入，并返回一个数组，其中包含每个样本的聚类标记。

3. dendrogram：绘制层次聚类的树状图。它接受一个连结矩阵作为输入，并根据层次聚类的结果绘制树形图。

除了这些方法之外，scipy.cluster.hierarchy模块还提供了一些用于计算距离矩阵和配对距离的函数，如pdist和cophenet。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import linkage
from scipy.cluster.hierarchy import dendrogram
from scipy.spatial.distance import pdist        # 引入pdist计算距离

X1,X2=[],[]
fr=open('Sklearn\km.txt')
for line in fr.readlines():
    lineArr=line.strip().split()
    X1.append([int(lineArr[0])])
    X2.append([int(lineArr[1])])
X=np.array(list(zip(X1,X2))).reshape(len(X1),2)
model=AgglomerativeClustering(n_clusters=3)
labels=model.fit_predict(X)

# print(labels)

# 绘制层次聚类树
variables=['X','Y']
df=pd.DataFrame (X,columns=variables,index=labels)
# print (df)            # df保存了样本点的坐标值和类别值，可打印出来看

# 使用完全距离矩阵
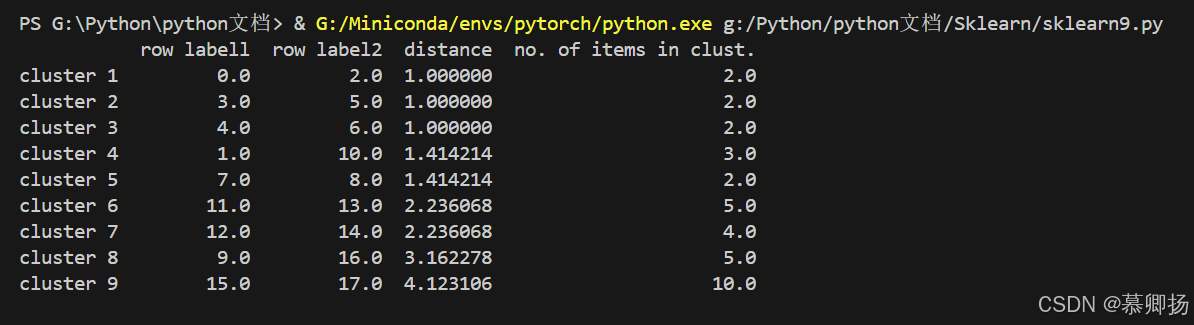
row_clusters=linkage(pdist(df,metric='euclidean'),method='complete')
print(pd.DataFrame(row_clusters,columns=['row labell','row label2','distance','no. of items in clust.'],index=['cluster %d'%(i+1) for i in range (row_clusters.shape[0])]))


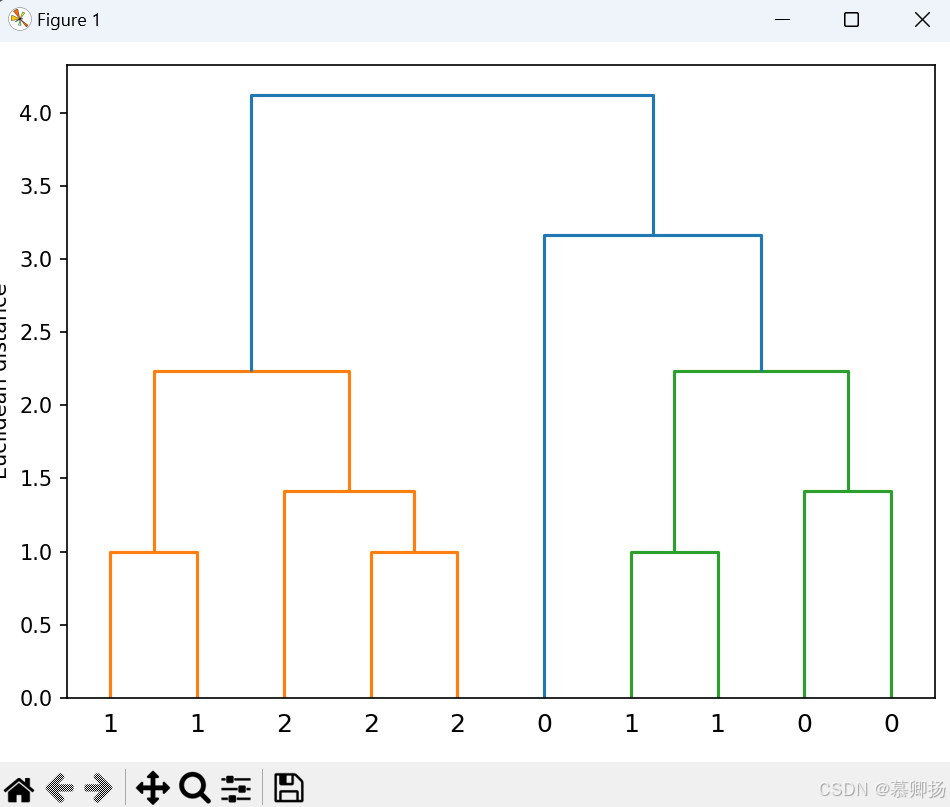
row_dendr=dendrogram(row_clusters,labels=labels)        # 绘制层次聚类树
plt.tight_layout()
plt.ylabel('Euclidean distance')
plt.show()

运行结果：

2.2.3 DataFrame数据结构

DataFrame是Pandas库中的一个数据结构，它类似于Excel中的二维表格，可以存储和操作二维数据。DataFrame由行索引和列索引组成，可以通过行索引和列索引来访问和操作数据。

DataFrame既可以从csv、excel等文件中读取数据，也可以从字典、列表等数据结构中创建。

下面是一个创建DataFrame的例子：

import pandas as pd

data = {'Name': ['Tom', 'John', 'Emily'],
        'Age': [23, 25, 27],
        'Country': ['USA', 'UK', 'Canada']}

df = pd.DataFrame(data)
print(df)

输出结果：

   Name  Age Country
0   Tom   23     USA
1  John   25      UK
2  Emily  27  Canada

注意：

• DataFrame的每一列都可以是不同的数据类型，例如上面的Name列是字符串类型，Age列是整数类型，Country列是字符串类型。

三、k-means聚类算法

k-means聚类算法最早由J.B. MacQueen于1967年提出，被广泛应用于数据分析和机器学习领域。k-means聚类算法是一种无监督学习算法，用于将数据集分为k个不重叠的簇，每个簇都具有相似的特征。它是一种迭代算法，以最小化簇内平方误差（SSE）为目标函数。

3.1 算法原理和实例

3.1.1 k-means聚类算法原理

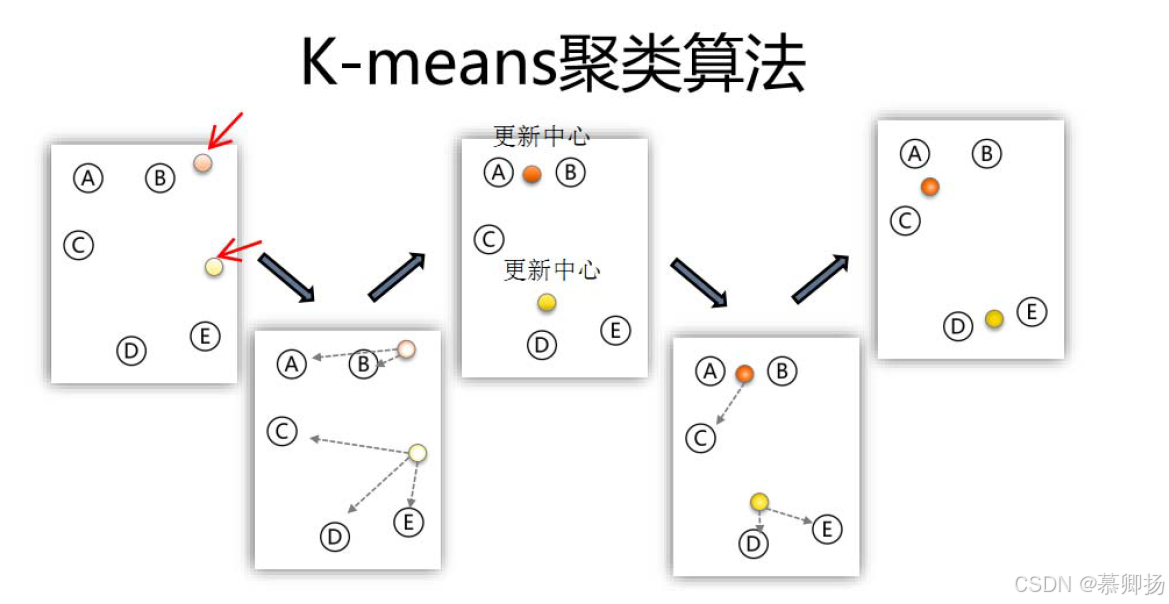
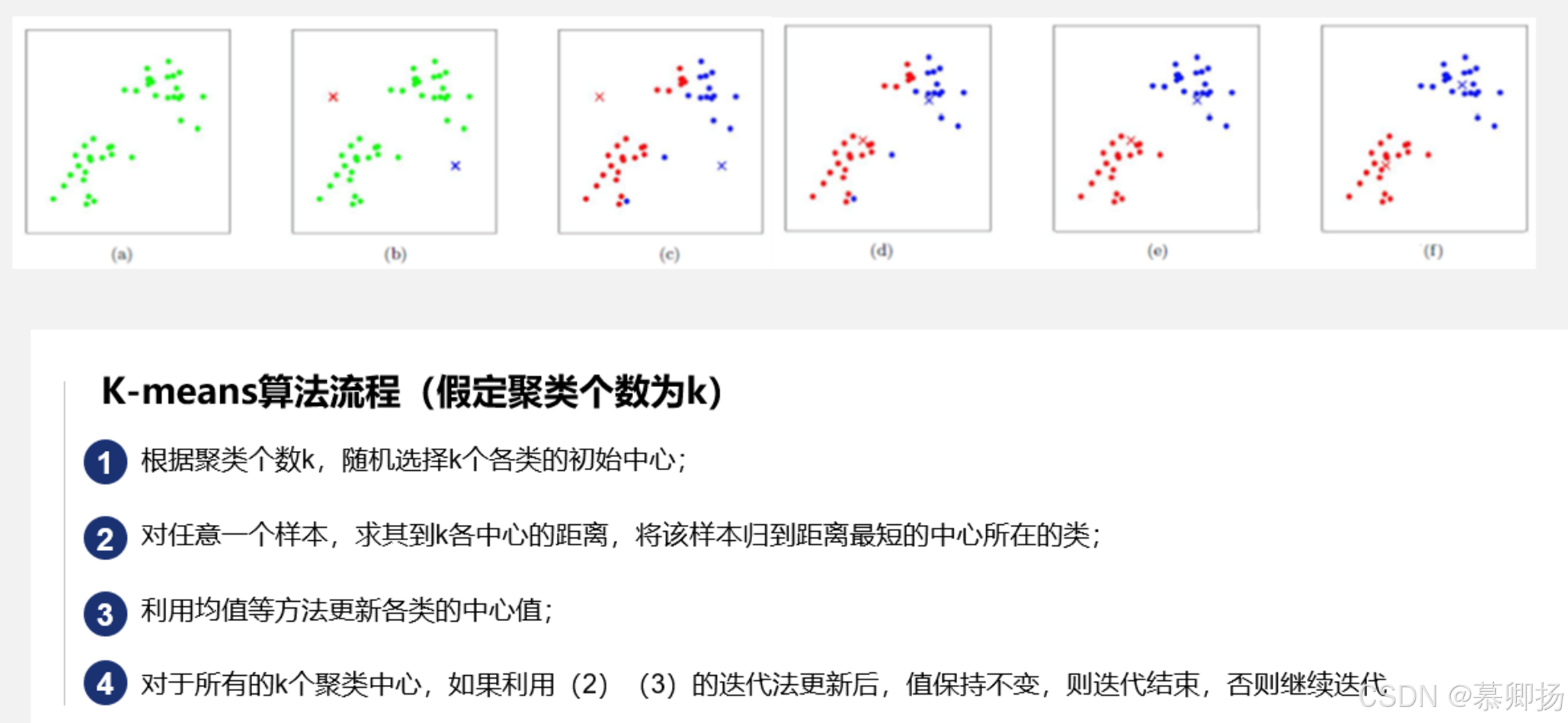
k-means聚类算法是一种迭代的优化算法，通过不断更新簇的中心点来划分数据集。其主要步骤如下：

1. 随机初始化：从数据集中随机选择K个样本作为初始的簇中心点。

2. 分配样本：对于每个样本，计算其与各个簇中心点的距离，将样本分配给距离最近的簇中心点所对应的簇。

3. 更新簇中心点：对于每个簇，计算该簇内所有样本的平均值，将其作为新的簇中心点。

4. 重复步骤2和步骤3，直到满足停止条件。停止条件可以是簇中心点不再变化或者迭代次数达到预定的值。

3.1.2 k-means聚类算法举例

假设有如下10个样本点的二维数据：(1, 2), (2, 1), (2, 3), (3, 2), (4, 4), (5, 5), (6, 6), (7, 7), (8, 7), (9, 9)

• 首先，我们随机选择两个初始聚类中心点，如选择(2, 1)和(6, 6)作为初始聚类中心。
• 接下来，对于每个样本点，计算其与两个聚类中心的欧几里得距离，然后将其归为距离较近的聚类中心所在的类别。
• 计算完成后，我们可以得到两个类别：
  • 类别1：(1, 2), (2, 1), (2, 3), (3, 2)
  • 类别2：(4, 4), (5, 5), (6, 6), (7, 7), (8, 7), (9, 9)
• 接下来，我们更新聚类中心，将每个类别中所有样本的坐标的平均值作为新的聚类中心。
  • 类别1的新聚类中心：(2.0, 2.0)
  • 类别2的新聚类中心：(6.5, 6.5)
• 然后，重复前面的步骤，计算每个样本与新的聚类中心的欧几里得距离，重新分配样本到类别中。
• 然后再次更新聚类中心，如此往复，直到聚类中心不再发生变化，满足终止条件。
• 最终，经过多次迭代后，我们可以得到如下的聚类结果：
  • 类别1：(1, 2), (2, 1), (2, 3), (3, 2)
  • 类别2：(4, 4), (5, 5), (6, 6), (7, 7), (8, 7), (9, 9)
• 其中，类别1的聚类中心为(2.0, 2.0)，类别2的聚类中心为(6.5, 6.5)

3.1.3 k-means聚类算法的优缺点

k-means聚类算法的优点：

1. 简单易实现：k-means算法是一种经典的聚类算法，实现起来相对简单。

2. 可解释性强：聚类结果直观明了，每个样本点都被分配到最近的聚类中心所在的类别中。

3. 可扩展性好：对于大规模的数据集，k-means算法可以通过并行计算来提高效率。

4. 对于凸形状的类别效果较好：k-means算法对于具有明显凸形状的类别，效果较好。

k-means聚类算法的缺点：

1. 需要预先确定聚类数量k：k-means算法需要提前指定聚类的数量，但在实际应用中，聚类数量往往是未知的。

2. 对初始聚类中心敏感：k-means算法的结果可能会受到初始聚类中心的选择影响，不同的初始聚类中心可能得到不同的最终结果。

3. 对异常值敏感：k-means算法对异常值比较敏感，异常值可能会对聚类结果产生较大的干扰。

4. 只适用于数值型数据：k-means算法只适用于数值型数据，对于包含非数值型特征的数据集，需要进行预处理或选择其他算法。

3.2 算法中k值的确定

k-Means算法中的k值是指聚类的簇数，也就是将数据集划分为多少个簇。确定k值是k-Means算法中的一个关键问题，一般可以使用以下方法来确定k值：

1. 观察数据集：直观上观察数据集的分布情况，根据数据的特点和目标来选择合适的k值。例如，如果数据集呈现出明显的分群特征，可以根据分群的数量确定k值。

2. 手肘法（Elbow Method）：通过计算不同k值下的簇内平方误差（SSE）来确定k值。在每个k值下，计算各个簇与其质心的距离平方之和，然后选择一个合适的k值，使得簇内平方误差开始显著下降而后趋于平缓。

3. 轮廓系数（Silhouette Coefficient）：通过计算各个样本的轮廓系数来评估聚类的质量，然后选择一个合适的k值。轮廓系数介于-1到1之间，值越大表示聚类效果越好。计算轮廓系数时，需要计算样本与同簇其他样本的平均距离（a）和样本与其他簇的最小平均距离（b），然后计算轮廓系数为(b-a)/max(a,b)。选择一个k值，使得整体的轮廓系数最大。

4. Gap统计量：通过计算数据集在不同k值下的Gap统计量来确定k值。Gap统计量是一种比较聚类结果与随机数据集的聚类结果的统计方法，选择一个k值，使得Gap统计量达到峰值。

3.3 算法的Sklearn实现

在Sklearn中，提供了两个k-means的算法，分别是K-Means和Mini Batch K-Means。

K-Means是传统的k-means算法，它使用了Lloyd's算法来进行聚类。该算法的原理是，首先随机选择k个样本点作为初始的聚类中心，然后将每个样本点分配到距离最近的聚类中心，再根据分配结果更新聚类中心的位置，重复以上步骤直到聚类中心的位置不再变化或者达到最大迭代次数。

Mini Batch K-Means是一种优化的k-means算法（MiniBatchKMeans），它使用了小批量随机梯度下降的方法来进行迭代。相比于传统的k-means算法，MiniBatchKMeans使用了一个小批量的样本点来更新聚类中心，从而减少了计算量和内存消耗。

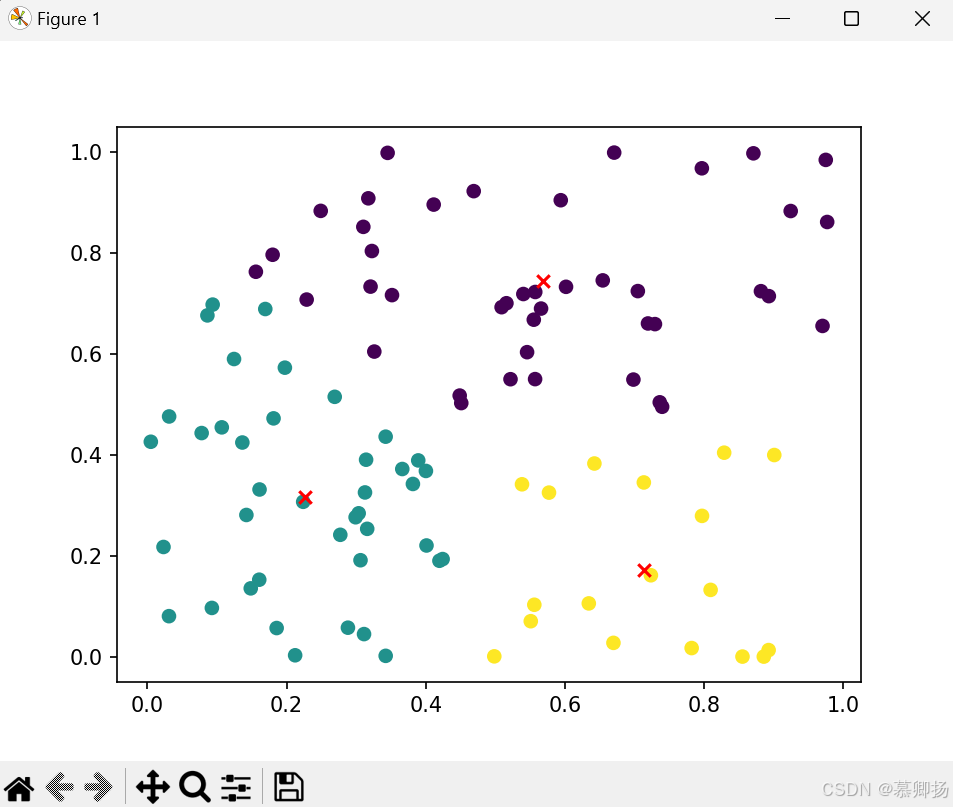
利用python的sklearn库实现kmeans聚类算法并绘制散点图：

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 随机生成一些样本数据
X = np.random.rand(100, 2)

# 创建KMeans对象，并指定聚类个数为3
kmeans = KMeans(n_clusters=3)

# 使用KMeans对象对样本数据进行聚类
kmeans.fit(X)

# 获取聚类结果
labels = kmeans.labels_

# 获取聚类中心点坐标
centers = kmeans.cluster_centers_

# 绘制散点图
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.scatter(centers[:, 0], centers[:, 1], marker='x', color='red')

plt.show()

运行结果：

首先使用numpy库生成了一些随机样本数据，然后创建了KMeans对象，并指定聚类个数为3。接着使用fit方法对样本数据进行聚类，得到聚类结果。再使用matplotlib库绘制散点图，其中散点的颜色由labels数组决定，聚类中心点用红色的x标记出来。最后调用plt.show()显示图像。